转载自知乎用户@林麦,@中微子
https://www.zhihu.com/question/20500497
作者:林麦
链接:https://www.zhihu.com/question/20500497/answer/24525658
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
最近复习看到卷积这块儿,说说我的理解。
如果随便给你两个函数让你算卷积,其实没什么具体意义,就是用某种规则实现某种运算而已。如果要探究物理意义,那么最好把它放到一个因果稳定的系统(就是从零之后才有值,而且收敛的那种)中,从单位冲击响应h(t)来看。我们都知道,将给定的一个函数x(t)与系统的h(t)卷积,得到的就是输出y(t),这利用了LSI系统满足的叠加定理。下面解释为什么卷积一下子就是输出。
(1)
对h(t)的一种理解是:它表征
影响因子。
所谓影响因子就是你给了一个输入,它在不同时间产生的影响力大小。首先要明白,当我们算某个时刻的响应的时候,它不仅与这个时刻的输入有关,还与之间所有在这个时刻存在影响因子的输入有关。例如,我们要求t=4时刻的输入y(4),那么
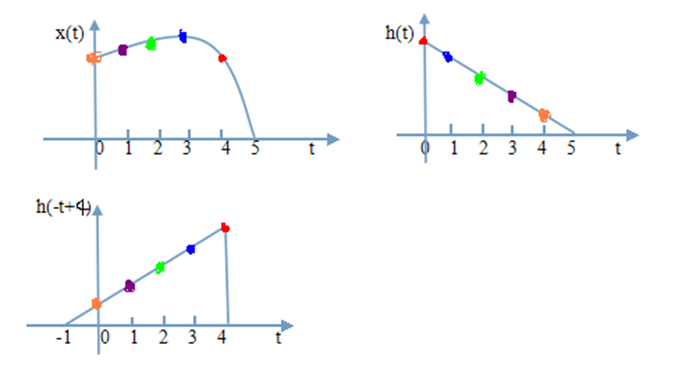
y(4)=x(4)h(0)+x(3)h(1)+x(2)h(2)+x(1)h(3)+x(0)h(4),注意,这个式子是错误的,正确的应该是无数时刻的积分,这里只领会精义就行了。看下面的图,相同颜色的是对应的输入与对应在t=4时刻的影响因子,x(4)当然对应的影响因子最大为h(0),x(3)对应的影响因子就相对小了为h(1),····x(0)对应的影响因子最小为h(4).它正好就是h(-t+4),就是反褶后右移4。为什么要反褶呢,因为隔着t=4越近的输入对应的影响因子在h(t)中隔的t=4越远,而且从上面的式子也能看出,括号里对应时刻的和为4,正好也是平移的大小。

所以说,卷积的工程意义就是指示了某个系统的响应特性,也就是在某时刻给个输入delta(t),它接下来会做出什么反应,反应持续多久,h(t)就表征了这些,也就是在不同时刻的影响因子。
作者:中微子
链接:https://www.zhihu.com/question/20500497/answer/45708002
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
不要试图直接从公式上去思考“翻转”的意义,回到
问题的起源
,你就会豁然开朗了。
打个比方,
往平静的水面里面扔石头。我们把水面的反应看作是一种冲击响应。
水面在t=0时刻石头丢进去的时候会激起高度为h(0)的波纹,但水面不会立马归于平静,随着时间的流逝,波纹幅度会越来越小,在t=1时刻,幅度衰减为h(1), 在t=2时刻,幅度衰减为h(2)……直到一段时间后,水面重复归于平静。
从时间轴上来看,我们只在t=0时刻丢了一块石头,其它时刻并没有做任何事,但在t=1,2….时刻,水面是不平静的,这是因为过去(t=0时刻)的作用一直持续到了现在。
那么,问题来了:
如果我们在t=1时刻也丢入一块石子呢?此时t=0时刻的影响还没有消失(水面还没有恢复平静)新的石子又丢进来了,那么现在激起的波浪有多高呢?答案是当前激起的波浪与t=0时刻残余的影响的叠加。那么t=0时刻对t=1时刻的残余影响有多大呢?
为了便于说明,接下来我们作一下两个假设:
1. 水面对于“单位石块”的响应是固定的
2. 丢一个两倍于的“单位石块”的石块激起的波纹高度是丢一个石块的两倍(即系统满足线性叠加原理)
现在我们来计算每一时刻的波浪有多高:
- t=0时刻:
y(0)=x(0)*h(0);
- t=1时刻:
当前石块引起的影响x(1)*h(0);
t=0时刻石块x(0)引起的残余影响x(0)*h(1);
y(1)=x(1)*h(0)+ x(0)*h(1);
- t=2时刻:
当前石块引起的影响x(2)*h(0);
t=0时刻石块x(0)引起的残余影响x(0)*h(2);
t=1时刻石块x(1)引起的残余影响x(1)*h(1);
y(2)=x(2)*h(0)+ x(1)*h(1)+x(0)*h(2);
……
- t=N时刻:
当前石块引起的影响x(N)*h(0);
t=0时刻石块x(0)引起的残余影响x(0)*h(N);
t=1时刻石块x(1)引起的残余影响x(1)*h(N-1);
y(N)=x(N)*h(0)+ x(N-1)*h(1)+x(N-2)*h(2)+…+x(0)*h(N);
这就是离散卷积的公式了
理解了上面的问题,下面我们来看看“翻转”是怎么回事:
当我们每次要丢石子时,
站在当前的时间点,系统的对我们的回应都是
h(0)
,时间轴之后的(h(1),h(2)…..)都是对未来的影响。而整体的回应要加上过去对于现在的残余影响。
现在我们来观察t=4这个时刻。
站在
t=0
时刻
看他对于未来(t=4)时刻(从现在往后4秒)的影响,可见是x(0)*h(4)
站在
t=1
时刻
看他对于未来(t=4)时刻的影响(从现在往后3秒),可见是x(1)*h(3)
站在
t=2
时刻
看他对于未来(t=4)时刻的影响(从现在往后2秒),可见是x(2)*h(2)
站在
t=3
时刻
看他对于未来(t=4)时刻的影响(从现在往后1秒),可见是x(3)*h(1)
所以
所谓的翻转只是因为你站立的现在是过去的未来,而因为
h(t)
始终不变,故h(1)
其实是前一秒的h(1)
,而前一秒的h(1)
就是现在,所以
从当前x(4)
的角度往左看,你看到的是过去的作用。h(t)未翻转前,
当从h(0)
往右看,你看到的是现在对于未来的影响,
当翻转h(t)
之后,从h(0)
往左看,你依次看到的越来越远的过去对现在的影响,而这个影响,与从x=4
向左看的作用影响相对应(都是越来越远的过去),作用与作用的响应就对应起来了,这一切的本质,是因为你站立的时间观察点和方向在变。