题目
原题链接:
点这里
题目陈述
大意:给定一颗树,然后每次随机删除一个节点,删除它的同时他的子树都会消失,每次删除的节点等概率,问删除掉所有节点的期望步数
样例解释
-
如果给定了一下这棵树
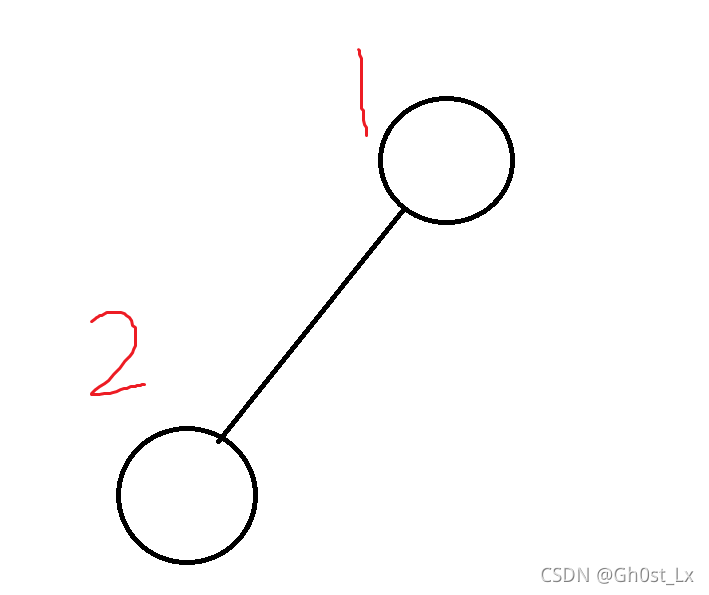
-
有两种删除这棵树的方法,
-
第一种方案:第一次就选择了
11
1
,整棵树直接被删除,概率为
12
\cfrac{1}{2}
2
1
,执行的步骤为
11
1
次,所以该方案的期望为
1∗
1
2
=
1
2
1*\cfrac{1}{2}=\cfrac{1}{2}
1
∗
2
1
=
2
1
次 -
第二种方案:第一次选择了
22
2
,第二次选择了
11
1
,因为第一选择
22
2
的概率为
12
\cfrac{1}{2}
2
1
,第二次只有一个节点,选择到
11
1
的概率为
100%
100\%
1
0
0
%
,故整个方案被实现的概率为
12
\cfrac{1}{2}
2
1
,执行的步骤为
22
2
次,该方案的步骤为
2∗
1
2
=
1
2*\cfrac{1}{2}=1
2
∗
2
1
=
1
-
总的期望步骤为所有方案的期望之和
12
+
1
=
1.5
\cfrac{1}{2}+1=1.5
2
1
+
1
=
1
.
5
-
如果给定了如下这棵树
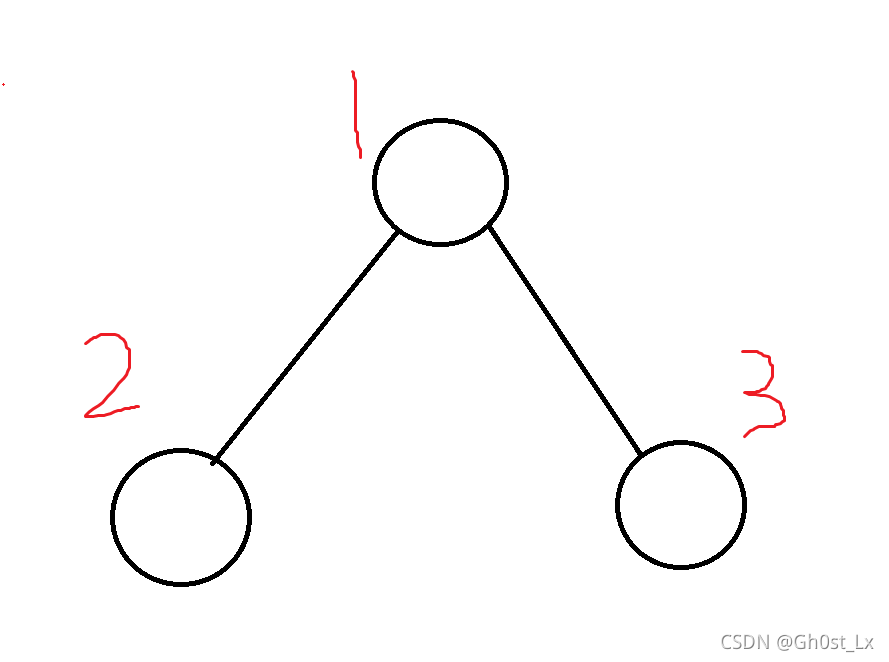
-
经过了上一个例子,相信你已经有一定感觉了
方案 被实现的概率 执行的步骤
1 1/3 1
2 1 1/6 2
3 1 1/6 2
2 3 1 1/6 3
3 2 1 1/6 3
-
最后总的期望步骤为
13
∗
1
+
1
6
∗
1
+
1
6
∗
2
+
1
6
∗
3
+
1
6
∗
3
=
2
\cfrac{1}{3}*1+\cfrac{1}{6}*1+\cfrac{1}{6}*2+\cfrac{1}{6}*3+\cfrac{1}{6}*3=2
3
1
∗
1
+
6
1
∗
1
+
6
1
∗
2
+
6
1
∗
3
+
6
1
∗
3
=
2
步
算法思路
- 首先我们考虑这样一个问题,对于一个节点,它什么时候会对我们的答案有贡献?
-
对于一个节点,在一整个完整的操作过程中,无非是
有被选到
和
没有被选到
,分别对应于
00
0
和
11
1
,我们用
ai
a_i
a
i
来表示这个值 -
我们假设第
ii
i
个点被选择到的概率为
pi
p_i
p
i
,那么最后它对答案的贡献
Ei
=
0
∗
(
1
−
p
i
)
+
1
∗
p
i
=
p
i
E_i=0*(1-p_i)+1*p_i=p_i
E
i
=
0
∗
(
1
−
p
i
)
+
1
∗
p
i
=
p
i
,总得答案就是
E=
∑
i
=
1
n
E
i
E=\sum_{i=1}^{n}E_i
E
=
∑
i
=
1
n
E
i
- 那么一个点被选到的概率有是多少呢?
-
我们知道,一个节点被删除掉的情况,只有他的
任意一个祖先被选择到
,或者
他自身被选择到
的时候,他就会删除掉。 -
换言之,反过来,它
被选择到
的时候,就说明
它的任意一个祖先节点都还在
-
接下来我们用
标记为黑色
代表
删除
-
我们随机生成一个由
11
1
到
nn
n
组成的
nn
n
个数的操作序列,我们首先找到第一个未被染成黑色的节点,然后将这个节点,,即其子树都染成黑色,重复上述操作,直至整个序列都是黑色。 -
对于节点
ii
i
,他能被选择到,则说明
它的任意一个祖先节点都在它的后面
-
因为
ii
i
节点有
de
e
p
[
i
]
−
1
deep[i]-1
d
e
e
p
[
i
]
−
1
个祖先,仅看
ii
i
节点和它的祖先的情况,考虑
插空法
,每个祖先前面都有一个空,最后一个祖先后面也有一个空,总共有
de
e
p
[
i
]
deep[i]
d
e
e
p
[
i
]
个空位可以插入。 -
只有
第一个空位
是满足该节点会
被选择到的
,即概率
pi
=
1
d
e
e
p
[
i
]
p_i=\cfrac{1}{deep[i]}
p
i
=
d
e
e
p
[
i
]
1
-
故最后的期望为
E=
∑
i
=
1
n
1
d
e
e
p
[
i
]
E=\sum_{i=1}^{n}\cfrac{1}{deep[i]}
E
=
∑
i
=
1
n
d
e
e
p
[
i
]
1
代码实现
// #pragma GCC optimize("O3")
#include <bits/stdc++.h>
#include <unordered_map>
#include <unordered_set>
using namespace std;
#define debug(x) cerr << #x << ": " << x << '\n'
#define bd cerr << "----------------------" << el
#define el '\n'
#define cl putchar('\n')
#define pb push_back
#define eb emplace_back
#define x first
#define y second
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define loop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define ceil(a, b) (a + (b - 1)) / b
#define ms(a, x) memset(a, x, sizeof(a))
#define inf 0x3f3f3f3f
#define db double
typedef long long LL;
typedef long double LD;
typedef pair<int, int> PII;
typedef pair<db, db> PDD;
typedef vector<int> vci;
const int N = 1e5 + 10, M = 2e6 + 10, E = 1e3 + 10, md = 1e9 + 7;
const double PI = acos(-1), eps = 1e-8;
int T, n, m;
int u, v;
vci g[N];
int h[N];
int dfs(int u)
{
for (auto v : g[u])
{
if (!h[v])
{
h[v] = h[u] + 1;
dfs(v);
}
}
}
int main()
{
cin.tie(0);
cout.tie(0);
cin >> n;
rep(i, 1, n - 1)
{
cin >> u >> v;
g[v].pb(u);
g[u].pb(v);
}
h[1] = 1;
db ans = 0;
dfs(1);
rep(i, 1, n)
{
ans += 1.0 / h[i];
}
printf("%.12lf",ans);
}