题目描述
输入一个表达式(用字符串表示),求这个表达式的值。
保证字符串中的有效字符包括[‘0’-‘9’],‘+’,‘-’, ‘*’,‘/’ ,‘(’, ‘)’,‘[’, ‘]’,‘{’ ,‘}’。且表达式一定合法。
输入:+3+2*{1+2*[-4/(8-6)+7]}
输出:25
思路
- 使用两个栈来维护计算过程:一个数字栈,用来存储操作数字;一个操作符栈,用来存储‘+’,‘-’, ‘*’,‘/’ ,‘(’,‘)’,‘[’, ‘]’,‘{’ ,‘}’等操作符
- 如果当前运算符优先级(‘*/’)高于栈顶运算符(‘+-‘)优先级,则将运算符入栈;反之,从数字栈中弹出两个数,从运算符栈中弹出栈顶运算符,进行运算,数字栈压入运算结果,符号栈压入当前运算符。重复该操作直到不满足条件。
- 出现左括号‘(’,则直接压入;出现右括号‘)’,则从数字栈中弹出两个数,从运算符栈中弹出栈顶运算符,进行运算,数字栈压入运算结果,重复该操作直到栈顶元素为左括号‘(’。
难点:
- 将数字从字符串中提取出来,而且要考虑正负号
- 运算符有优先级:有括号先算括号里的,再算乘除,最后加减,要满足从左往右运算顺序
注意:由于有除法运算,应该使用double格式来保存计算结果
使用到的字符串操作函数
find()与find_first_of()
|
string (1) |
size_t find (const string& str, size_t pos = 0) const noexcept; |
|---|---|
|
c-string (2) |
size_t find (const char* s, size_t pos = 0) const; |
|
buffer (3) |
size_t find (const char* s, size_t pos, size_type n) const; |
|
character (4) |
size_t find (char c, size_t pos = 0) const noexcept; |
string s = "hello world!";
cout << s.find('o') << endl;//4
cout << s.find('o', 5) << endl;//7
cout << s.find("world") << endl;//6
cout << s.find("word") << endl;//4294967295,未找到
cout << s.find_first_of("word") << endl;//4,“wor” 出现在原字符串中,
cout << s.find_last_of('o') << endl;//7在当前字符串s中搜索传入参数字符串或者字符在s中首次出现的下标,与find_first_of()不同的是,find_first_of()找到了首个匹配的实例之后就不找了,就认定找寻成功,返回首个字符的下标,而find()则是要求完全匹配。如果输入了pos参数,则从下标pos开始查找。
查找失败:返回string::npos
static const size_t npos = -1;
//npos is a static member constant value with the greatest possible value for an element of type size_t.
npos是一个静态成员常量,其值为size_t类型的最大值:4294967295,用来表示没找到元素。
substr()
截取字符串
string substr (size_t pos = 0, size_t len = npos) const;第一个参数pos是开始截取的位置下标,第二个参数len是截取的长度 ,若len==npos,意思是截取字符串从pos直到末尾
stoi()与stod()
将字符串转成int类型或double类型
实现代码
#include<iostream>
#include<stack>
#include<string>
using namespace std;
string nums = "0123456789";
//比较函数,用于比较当前操作符和栈顶操作符的优先级
//如果当前操作符优先级大于栈顶优先级,返回false
//如果栈顶操作符为左括号(
//如果当前操作符优先级小于栈顶优先级,true
//还要满足从左往右计算顺序,如果当前操作符与栈顶操作符为同级关系,返回true
//返回true说明此时需要将栈顶操作符弹出,用于计算
bool cmp(char top, char now){
if(top == '('){
return false;
}else if((top == '-' || top == '+') && (now == '*' || now == '/')){
return false;
}
return true;
}
//计算,从数字栈中弹出两个数字,操作符栈中弹出操作符
void calculate(stack<double> &num,stack<char> &op){
// 数字栈中数字的顺序也有要求
// 第一个弹出的数字在后面,第二个弹出的在前面
double b = num.top();
num.pop();
double a = num.top();
num.pop();
char c = op.top();
op.pop();
if(c == '+') a = a+b;
else if(c == '-') a = a-b;
else if(c == '*') a = a*b;
else if(c == '/') a = a/b;
//将结果放入数字栈
num.push(a);
return ;
}
int main(void){
string s;
while(getline(cin, s)){
//数字栈
stack<double> num_stk;
//操作符栈
stack<char> op_stk;
//预处理,将算式用括号括起来
op_stk.push('(');
s += ')';
//算式的第一个应该是数字
bool isNextOp = false;
for(int i=0; i<s.size(); ++i){
//左括号的话,直接压入操作符栈,将大中小括号都当做小括号处理
if(s[i] == '(' || s[i] == '[' || s[i] == '{'){
op_stk.push('(');
}
//右括号的话就可以开始计算,直到遇到与之对应的左括号
else if(s[i] == ')' || s[i] == ']' || s[i] == '}'){
while(op_stk.top() != '(') //计算
calculate(num_stk,op_stk);
//弹出此时的(
op_stk.pop();
}
//除括号外,数字和操作符应该是间隔排列的,而且算式的第一个应该是数字
//若没有括号,需要考虑操作符优先级问题,并且是从左往右计算
else if(isNextOp){
while(cmp(op_stk.top(),s[i])){
//计算
calculate(num_stk,op_stk);
}
op_stk.push(s[i]);
isNextOp = false;
}
//将数字从字符串中提取出来
else{
int j = i;
//+ -符号可能是正负符号
if(s[j] == '+' || s[j] == '-') ++i;
//数字可能有多位,在0-9中
while(nums.find(s[i]) != nums.npos) ++i;
//i和j之间的字符即为数字
//将数字提取,并压入数字栈
//num_stk.push(stod(nums.substr(j,i-j)));
num_stk.push((double)stoi(s.substr(j,i-j)));
--i;
//当前为数字,所以下一个为操作符
isNextOp = true;
}
}
//数字栈顶的元素即为最后结果
cout<<num_stk.top()<<endl;
}
return 0;
}
算法动图
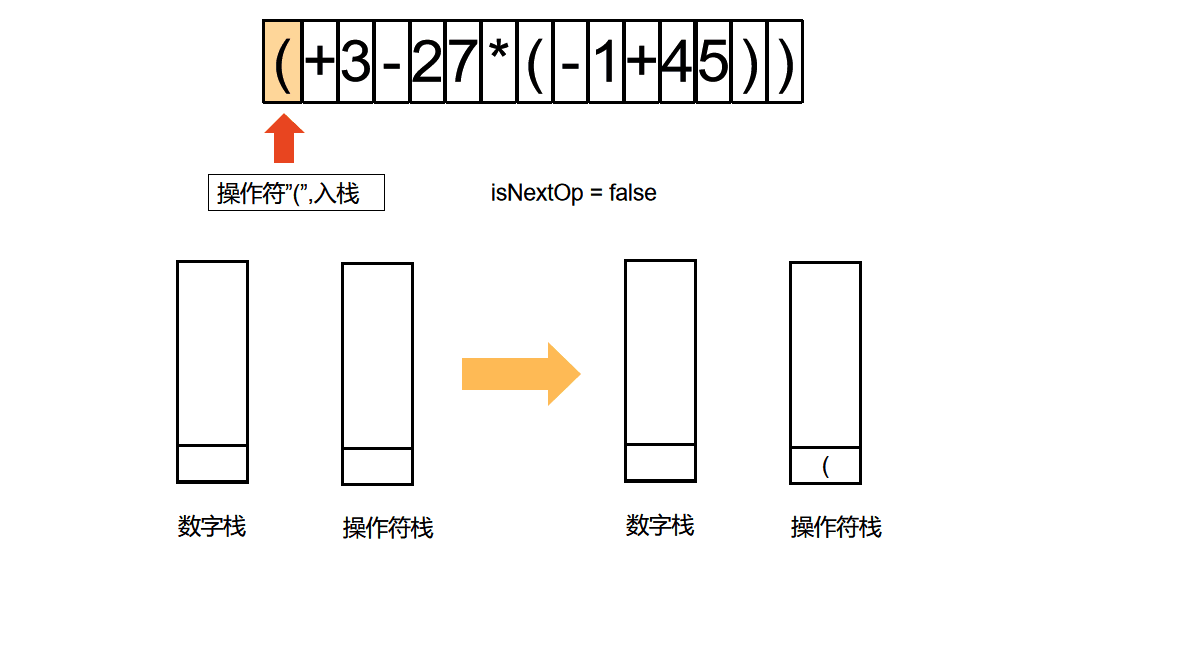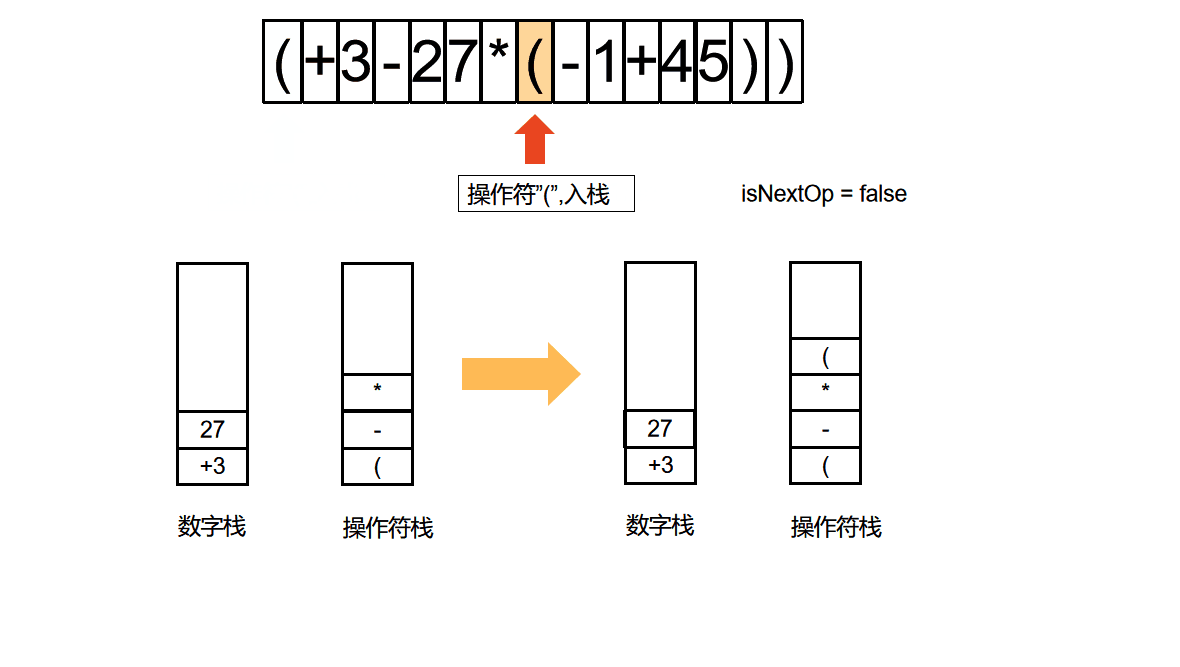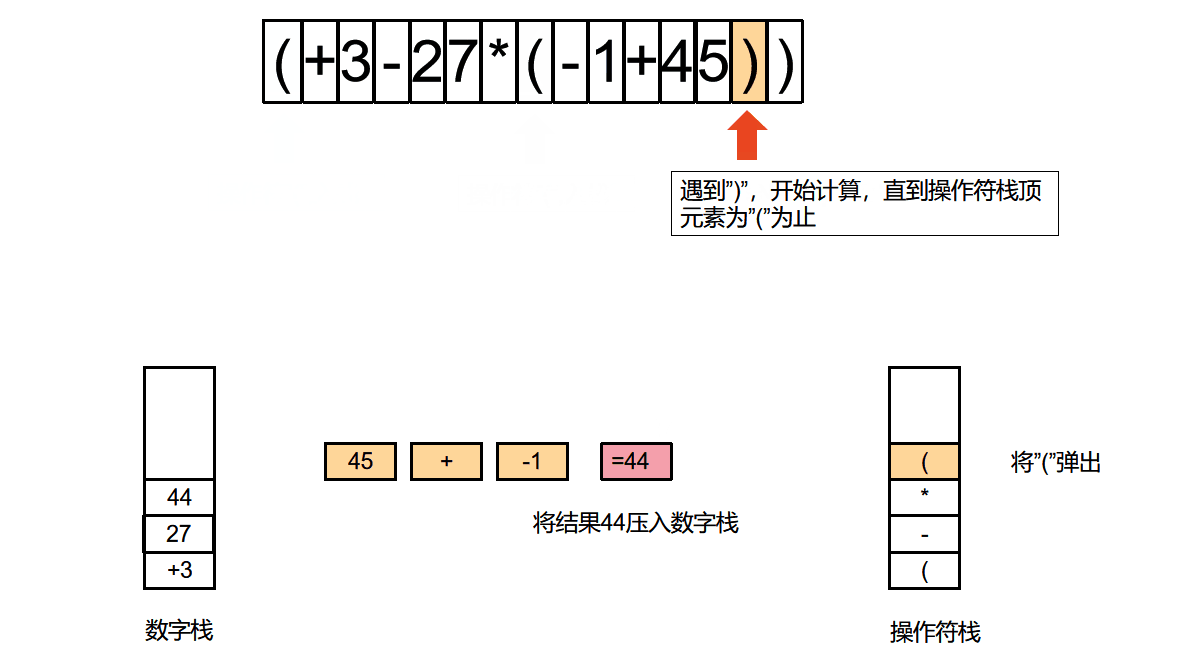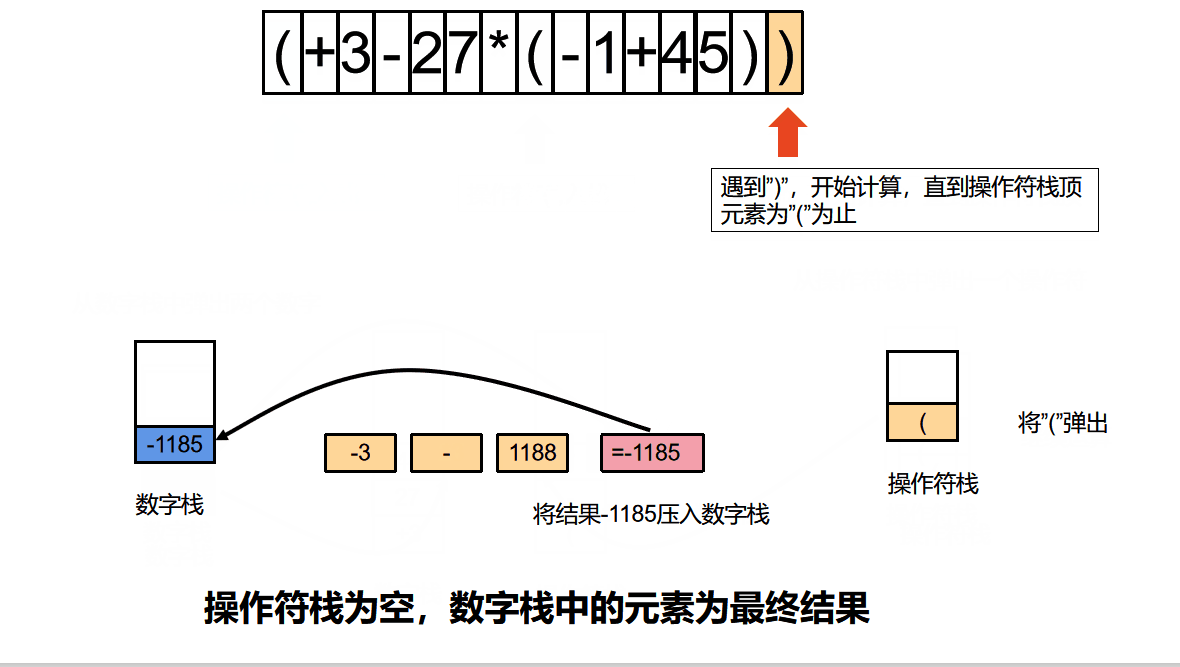
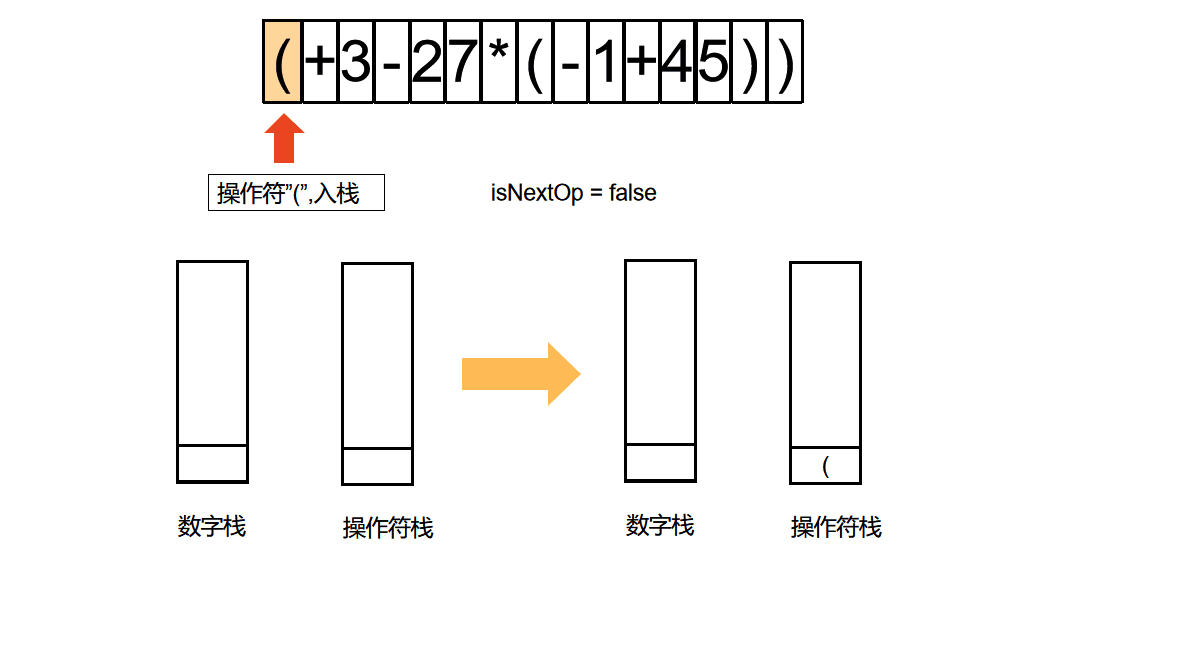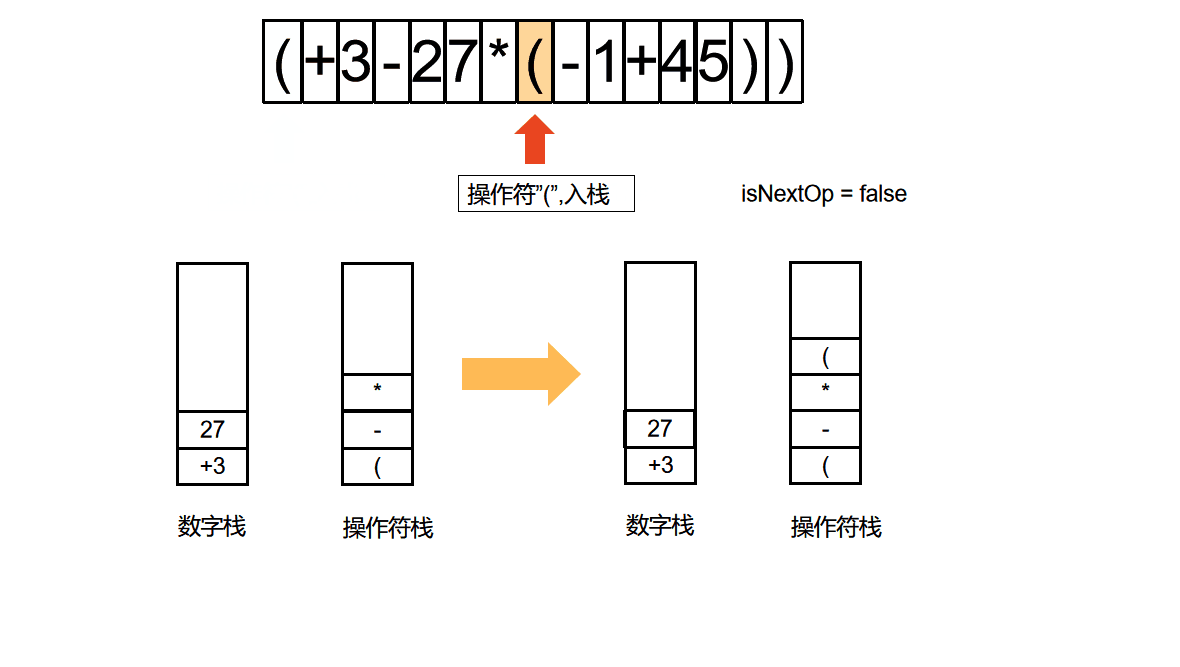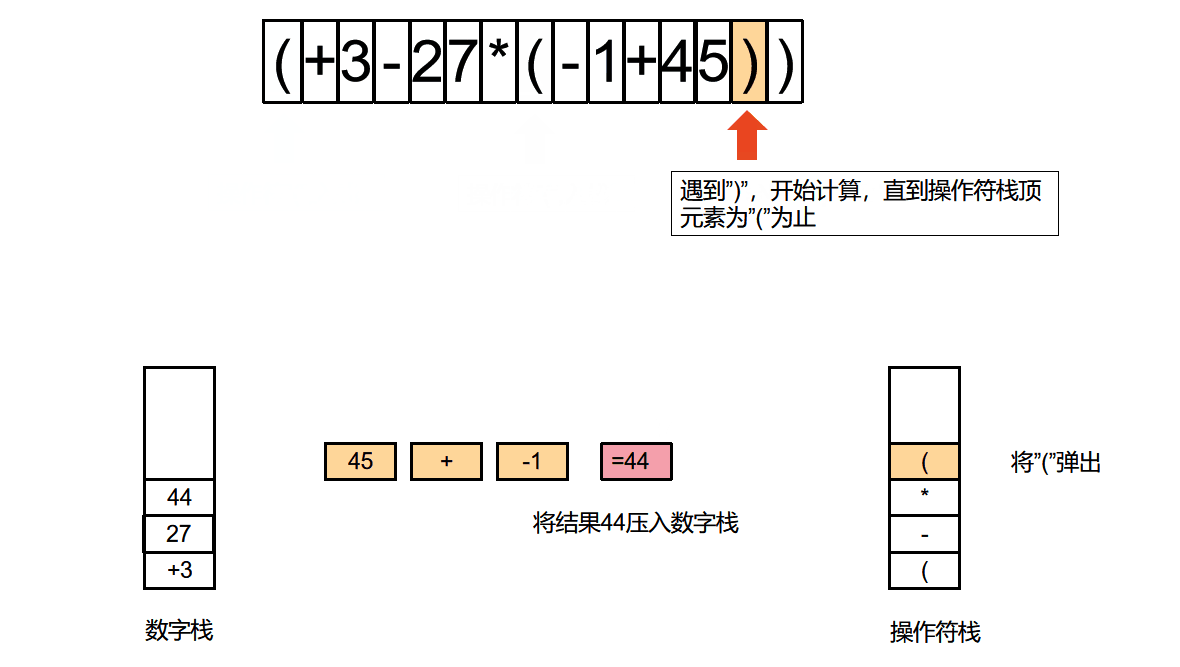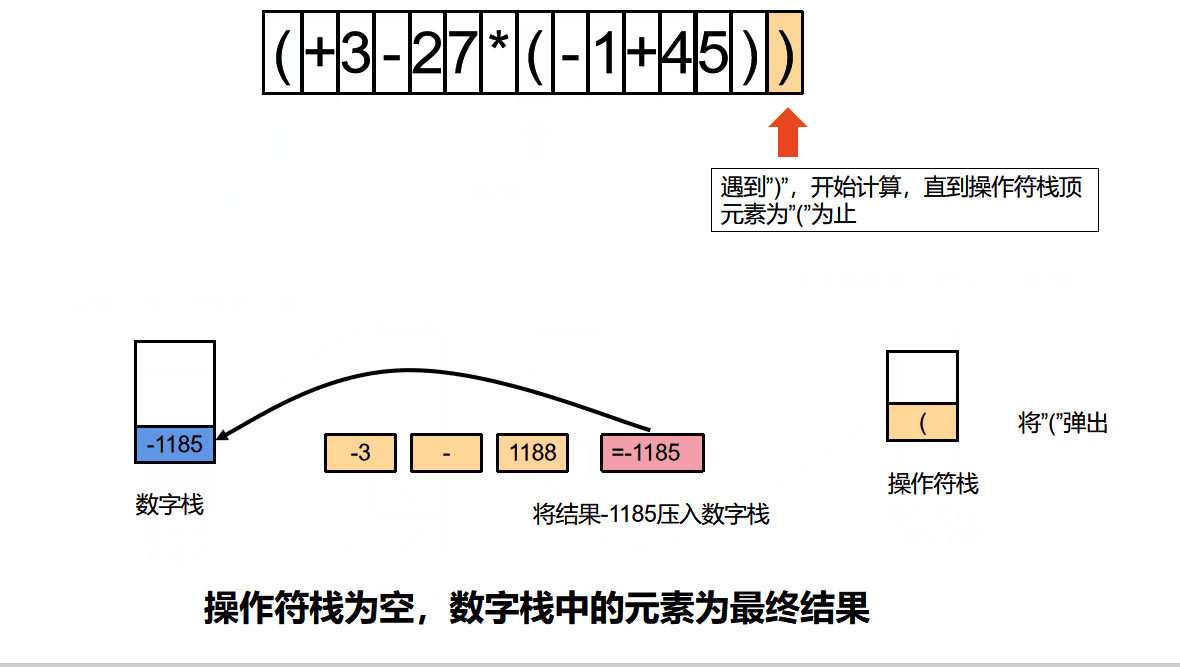
算法动图制作方法
在网上经常看见别人写的算法图解动图,本以为有专门的软件可以用,但是没有找了一圈并没有发现这种软件。
网上的一些动图开源项目:
于是自己决定采用土办法,使用PPT+录屏软件来制作算法动图:
发现一个很好用的gif录屏工具:
screentogif
下载链接:
ScreenToGif

首先在PPT中将算法步骤一张一张描绘出来,然后使用gif录屏软件制即可:

当前算法PPT下载地址: