图像处理理论（一）——直方图、二值化、滤波基础

http://antkillerfarm.github.io/

对比度和亮度

g (i, j) = a \times f (i, j) + b

$g(i,j)=a\times f(i,j)+b$

上式中

$f(i,j)$
和

$g(i,j)$
表示位于第i行，第j列的像素。上述线性变换中，a表示对比度，b表示亮度。

邻域

⎡ ⎣ ⎢ A 0 A 3 A 5 A 1 A A 6 A 2 A 4 A 7 ⎤ ⎦ ⎥

$\left[ \begin{array}{ccc} A_0&A_1&A_2\\ A_3&A&A_4 \\ A_5&A_6&A_7\end{array} \right]$

$A_0$
~

$A_7$
被称作像素A的1度8-邻域(即

$U(A,1)$
)，相应的上下左右的四个像素

$A_1$
、

$A_3$
、

$A_4$
、

$A_6$
被称作像素A的1度4-邻域。下文如无特别指出，邻域均为8-邻域。

定义

$U^+(A,N)=A\bigcup\limits_{i=1}^N U(A,i)$
。

U (A, 2)

$U(A,2)$
的定义如下：

如果

$B\in U(A,1)\land C\in U(B,1)\land C\notin U^+(A,1)$
，那么

$C\in U(A,2)$
。

类似的

$U(A,N)$
的定义为：

如果

$B\in U(A,N-1)\land C\in U(B,1)\land C\notin U^+(A,N-1)$
，那么

$C\in U(A,N)$
。

这里的N被称为度数，也就是两点间的距离，即

$L(A,C)=N$
。

卷积算子

卷积（Convolution)算子

g = f * h

$g=f\ast h$

的定义为：

g (i, j) = \sum k, l f (i - k, j - l) h (k, l)

$g(i,j)=\sum_{k,l}f(i-k,j-l)h(k,l)$

显然

f * h = f \otimes r o t 180 (h)

$f\ast h=f\otimes rot180(h)$

其中，rotN表示将矩阵元素绕中心逆时针旋转N度，显然这里的N只有为90的倍数，才是有意义的。

灰度化

以RGB格式的彩图为例，通常灰度化采用的方法主要有：

方法1：

$Gray=(R+G+B)/3$

方法2：

$Gray=max(R,G,B)$

方法3：

$Gray=0.299R+0.587G+0.114B$
（这种参数考虑到了人眼的生理特点）

灰度直方图

灰度直方图是灰度级的函数，描述图像中该灰度级的像素个数（或该灰度级像素出现的频率）：其横坐标是灰度级，纵坐标表示图像中该灰度级出现的个数（频率）。

一维直方图的结构表示为:

N (P) = [n 1, n 2, \dots, n L - 1]

$N(P)=[n_1,n_2,\dots,n_{L-1}]$

N = \sum i = 0 L - 1 n i, p i = n i N

$N=\sum_{i=0}^{L-1}n_i,p_i=\frac{n_i}{N}$

其中，L为灰度级的个数，

$n_i$
为每个灰度的像素个数，其出现概率为

$p_i$
。

同理，可将灰度直方图的概念推广到单独的颜色通道，即所谓的颜色直方图。如下图所示：

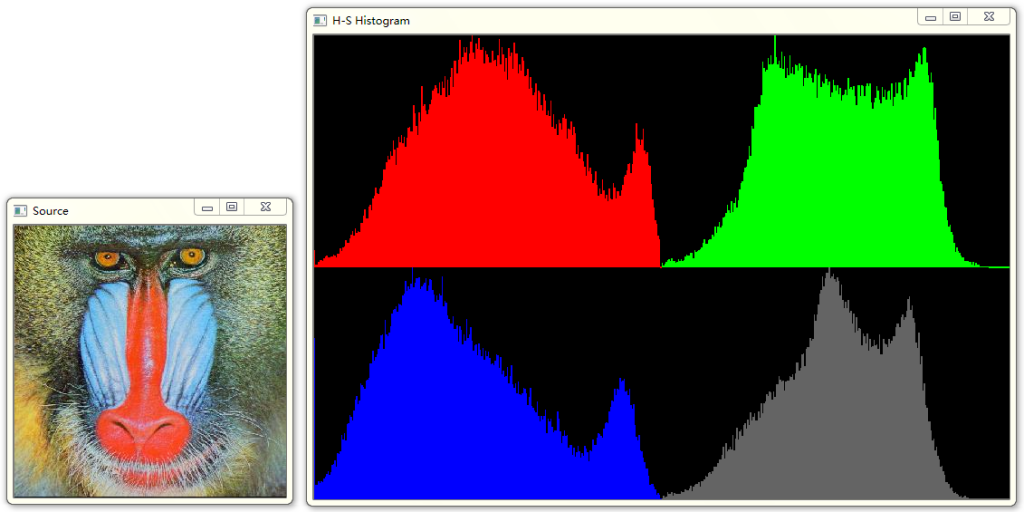
这里写图片描述

直方图均衡化

直方图均衡化是通过灰度变换将一幅图像转换为另一幅具有均衡直方图，即在每个灰度级上都具有尽可能相同的象素点数（即均匀分布）的过程。

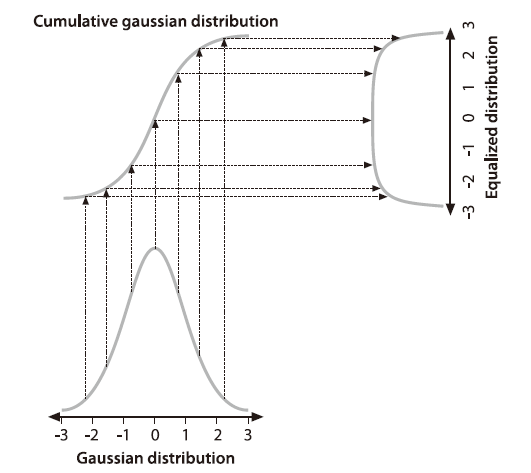
这里写图片描述

上图展示的是，将一个高斯分布的直方图转换为均匀分布的直方图的过程，其中累积分布函数起到了桥梁作用。事实上，任意分布的函数都可以通过这样的方式转换为另一种分布函数。而直方图均衡化，就是将其他分布函数的直方图转换成均匀分布的直方图的过程。

具体计算方法如下：

1.建立图像灰度直方图。

2.计算累积分布函数

$P(k)$
。

$P(k)=\sum_{i=0}^{k}p_i$

3.生成新的灰度和旧的灰度的对应关系数组。

$T(i)=P(i)*L$

其中

$T(i)$
表示对应原来的灰度i的新灰度值。

4.用新的灰度值替换旧的灰度值。

直方图均衡化的效果如下所示：

这里写图片描述

原图

这里写图片描述

效果图

直方图均衡化主要处理那些曝光不够或者曝光过度的图片，可以显著提高这些图片的对比度。但其本质是扩大了量化间隔，而量化级别反而减少了，因此，原来灰度不同的象素经处理后可能变的相同，形成了一片的相同灰度的区域，各区域之间有明显的边界，从而出现了伪轮廓。这种效应也称作“灰度吞噬效应”。

彩色直方图的均衡化有以下几种方法：

1.统计所有RGB颜色通道的直方图的数据并做均衡化运算，然后根据均衡化所得的映射表分别替换R、G、B通道颜色值。

2.分别统计R、G、B颜色通道的直方图的数据并做均衡化运算，然后根据R、G、B的映射表分别替换R、G、B通道颜色值。

3.用亮度公式或求RGB的平均值的方式计算亮度通道，然后统计亮度通道的直方图的数据并做均衡化运算，然后根据映射表分别替换R、G、B通道颜色值。

二值化

二值图也就是黑白图。将灰度图转换成黑白图的过程，就是二值化。二值化的一般算法是：

g = {0, 1, f \leq t f > t

$g=\begin{cases} 0, & f\le t \\ 1, & f>t \\ \end{cases}$

其中

t

$t$
被称为阀值。阀值的确定方法有下面几种。

Otsu法（大津法或最大类间方差法）

该算法是一种动态阈值分割算法。它的主要思想是按照灰度特性将图像划分为背景和目标2部分（这里我们将

f \leq t

$f\le t$
的部分称为背景，其他部分称为目标。），选取门限值，使得背景和目标之间的方差最大。

注：Nobuyuki Otsu，东京大学博士，先后在筑波大学和东京大学担任教授。

其步骤如下：

1.建立图像灰度直方图。

2.计算背景和目标的出现概率。

p A = \sum i = 0 t p i, p B = \sum i = t + 1 L - 1 p i = 1 - p A

$p_A=\sum_{i=0}^{t}p_i,p_B=\sum_{i=t+1}^{L-1}p_i=1-p_A$

其中，A和B分别表示背景部分和目标部分。

3.计算A和B两个区域的类间方差。

ω A = \sum t i = 0 i p i p A, ω B = \sum L - 1 i = t + 1 i p i p B (公 式 1)

$\omega_A=\frac{\sum_{i=0}^{t}ip_i}{p_A},\omega _B=\frac{\sum_{i=t+1}^{L-1}ip_i}{p_B}(公式1)$

公式1分别计算A和B区域的平均灰度值；

ω 0 = p A ω A + p B ω B = \sum i = 0 L - 1 i p i (公 式 2)

$\omega_0=p_A\omega_A+p_B\omega_B=\sum_{i=0}^{L-1}ip_i(公式2)$

公式2计算灰度图像全局的灰度平均值；

σ 2 = p A (ω A - ω 0) 2 + p B (ω B - ω 0) 2 (公 式 3)

$\sigma^2=p_A(\omega_A-\omega_0)^2+p_B(\omega_B-\omega_0)^2(公式3)$

公式3计算A、B两个区域的类间方差。

4.针对每一个灰度值，计算类间方差。选择方差最大的灰度值，作为阀值

$t$
。

一维交叉熵值法

对于两个分布R和Q，定义其信息交叉熵D如下：

R = {r 1, r 2, \dots, r n}, Q = {q 1, q 2, \dots, q n}

$R=\{r_1,r_2,\dots,r_n\},Q=\{q_1,q_2,\dots,q_n\}$

D (Q, R) = \sum k = 1 n q k l o g 2 q k r k

$D(Q,R)=\sum_{k=1}^{n}q_k log_2\frac{q_k}{r_k}$

注：严格来说，这里定义的是相对熵(relative entropy)，又称为KL散度（Kullback-Leibler divergence）或KL距离，是两个随机分布间距离的度量。从公式可以看出，KL距离和经典概率论中的二项分布有很密切的关系。

交叉熵的严格定义参见：

https://en.wikipedia.org/wiki/Cross_entropy

http://www.voidcn.com/blog/rtygbwwwerr/article/p-5047519.html

二值化过程实际上就是从分布

$R=\{r_1,r_2,\dots,r_L\}$
到分布

$Q=\{q_A,q_B\}$
的过程。

因此

D (t) = \sum i = 0 t i p i l o g 2 (p i ω A) + \sum i = t + 1 L - 1 i p i l o g 2 (p i ω B)

$D(t)=\sum_{i=0}^{t}ip_i log_2(\frac{p_i}{\omega_A})+\sum_{i=t+1}^{L-1}ip_i log_2(\frac{p_i}{\omega_B})$

其中，使得D最小的t即为最小交叉熵意义下的最优阈值。

二维Otsu法

Otsu法对噪音和目标大小十分敏感，它仅对类间方差为单峰的图像产生较好的分割效果。

当目标与背景的大小比例悬殊时，类间方差准则函数可能呈现双峰或多峰，此时效果不好，但是Otsu法是用时最少的。

二维Otsu法,在考虑像素点灰度级p的基础上,增加了对像素点邻域平均像素值s的考虑。

如果p比s大很多，说明像素的灰度值远远大于其临域的灰度均值，故而该点很可能是噪声点，反之如果p比s小很多，即该点的像素值比其临域均值小很多，则说明是一个边缘点。这两种点在后续的计算中，都要去除掉。

二维Otsu法的推导过程极为复杂，可参见：

http://blog.csdn.net/likezhaobin/article/details/6915755

方框滤波（Box Filter）

g = f \otimes h, h = α ⎡ ⎣ ⎢ ⎢ ⎢ 11 \dots 1 11 \dots 1 11 \dots 1 \dots \dots \dots \dots 11 \dots 1 ⎤ ⎦ ⎥ ⎥ ⎥, α = {1 S U M ( h ), 1, normalize=true normalize=false

$g=f\otimes h,h=\alpha \begin{bmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & 1 & 1 & \cdots & 1 \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 1 & 1 & 1 & \cdots & 1 \end{bmatrix} ,\alpha = \begin{cases} \frac{1}{SUM(h)}, & \text{normalize=true} \\ 1, & \text{normalize=false} \\ \end{cases}$

当normalize=true时的方框滤波，也被称为均值滤波（Mean filter）。

高斯滤波（Gauss filter）

高斯平滑滤波器对于抑制服从正态分布的噪声非常有效。

正态分布的概率密度函数为：

f (x) = 1 2 π - - \sqrt σ e - ( x - μ ) 2 2 σ 2

$f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

其标准化后的概率密度函数为：

f (x) = 1 2 π - - \sqrt e - x 2 2

$f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$

标准二维正态分布的概率密度函数为：

f (x, y) = 1 2 π e - x 2 + y 2 2 = f (x) f (y)

$f(x,y)=\frac{1}{2\pi}e^{-\frac{x^2+y^2}{2}}=f(x)f(y)$

这个公式表明标准二维正态分布，可以分解为两个正交方向上的标准一维正态分布。也就是说标准二维正态分布不仅是中心对称，也是轴对称的。

正态分布的性质：

1.两个正态分布密度的乘积、卷积，还是正态分布。

2.正态分布的傅立叶变换、共轭分布，还是正态分布。

3.正态分布和其它具有相同均值、方差的概率分布相比，具有最大熵。

4.二项分布、泊松分布、

$\chi^2$
分布、t分布等在样本增大的情况下，都趋向于正态分布。

正态分布的相关内容可参考：

正态分布的前世今生

标准正态分布的最佳逼近符合杨辉三角，比如一个具有5个点的一维标准正态分布的最佳逼近为：

[14641]

$\left[ \begin{array}{ccccc} 1&4&6&4&1\end{array} \right]$

同理，最常用的3*3高斯滤波h矩阵为：

⎡ ⎣ ⎢ 121 ⎤ ⎦ ⎥ \times [121] = ⎡ ⎣ ⎢ 121242121 ⎤ ⎦ ⎥

$\left[\begin{array}{c} 1\\2\\1\end{array} \right]\times \left[\begin{array}{ccc} 1&2&1\end{array} \right]=\left[\begin{array}{ccc} 1&2&1\\ 2&4&2 \\ 1&2&1\end{array} \right]$

其归一化形式为：

⎡ ⎣ ⎢ 0.0625 0.125 0.0625 0.125 0.25 0.125 0.0625 0.125 0.0625 ⎤ ⎦ ⎥

$\left[\begin{array}{ccc} 0.0625&0.125&0.0625\\ 0.125&0.25&0.125 \\ 0.0625&0.125&0.0625\end{array}\right]$

从效果来说，高斯滤波可产生类似毛玻璃的效果。

中值滤波（Median filter）

中值滤波是一种典型的非线性滤波技术，对于斑点噪声（speckle noise）和椒盐噪声（salt-and-pepper noise）来说尤其有用，对滤除脉冲干扰及图像扫描噪声非常有效，也常用于保护边缘信息。

以3*3的滤波窗口为例，计算以点

$[i,j]$
为中心的像素中值步骤如下：

1）对

$U^+(A,1)$
的9个像素点

$a_0\sim a_8$
，按强度值大小排列像素点，得到有序数组

$A_0\sim A_8$

2）选择排序像素集的中间值

$A_4$
作为点

$[i,j]$
的新值。

从效果来说，中值滤波可产生类似油彩画的效果。

上面这些滤波的效果如图所示：

这里写图片描述

原文链接：https://blog.csdn.net/antkillerfarm/article/details/52274740

对比度和亮度

邻域

相关算子

卷积算子

灰度化

灰度直方图

直方图均衡化

二值化

Otsu法（大津法或最大类间方差法）

一维交叉熵值法

二维Otsu法

方框滤波（Box Filter）

高斯滤波（Gauss filter）

中值滤波（Median filter）

你可能也喜欢