系列教程来自某学院,侵权删除。
学习完这一系列课程再去看VINS才能做到不吃力,不然直接撸网上的各种VINS解析完全云里雾里-_-!
前一讲中有提到整个残差函数由三部分组成,其中第一部分就是滑动窗口的先验,这一讲主要就是讲如何在去除一帧信息的时候向整个残差添加约束。
高斯分布与信息矩阵
首先对SLAM问题进行一个概率建模,利用贝叶斯的理论。
考虑某个状态
ξ \xi
ξ
,以及一次与该变量相关的观测
r i r_i
r
i
。由于噪声的存在,观测服从概率分布
p ( r i ∣ ξ ) p (r_i |ξ)
p
(
r
i
∣
ξ
)
。那么对与多次观测整个r的似然概率表达式为:
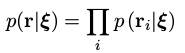
这里的
r = ( r 1 , . . . , r n ) T r=(r_1,…,r_n)^T
r
=
(
r
1
,
.
.
.
,
r
n
)
T
,根据贝叶斯法则,后验概率可表示为:
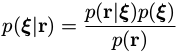
p ( ξ ) p(\xi )
p
(
ξ
)
是状态的先验信息,那么系统最优估计可以经过一些变换得到最小二乘的形式:
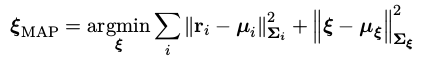
这时的待估计的机器人状态
ξ \xi
ξ
可以用下面的增量方程求解:
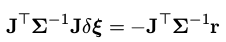
这里我们可以注意到和上一讲中的形式相比它多了一个协方差矩阵的逆
Σ − 1 \mathbf \Sigma^{-1}
Σ
−
1
,这是因为之前并没有考虑噪声,直接认为观测值r和
ξ \xi
ξ
相等,协方差矩阵的逆我们称之为
信息矩阵
,记为
Λ \Lambda
Λ
。
滑动窗口算法
图优化的例子
下面用一个例子来进行滑动窗口的理解:
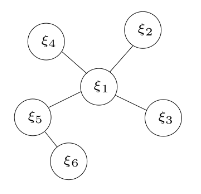
对于这样一个图结构,其中每个顶点代表一个待优化变量,可以看做机器人的姿态,边表示顶点之间构成的残差。这里的图结构可以类比十四讲中讲过的位姿图,不包含路标点在其中,每个边的约束就是由视觉和IMU构成的,所以实际