datawhale-吃瓜教程-支持向量机
Task01:概览西瓜书+南瓜书第1、2章
Task02:详读西瓜书+南瓜书线性模型
Task03:详读西瓜书+南瓜书决策树
Task04:详读西瓜书+南瓜书神经网络
Task05:详读西瓜书+南瓜书支持向量机
一、基本形式
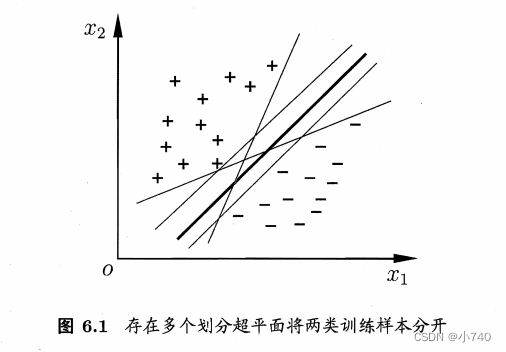
如图6.1,“+”号,“-”号表示不同类别的样本点,将样本点按类别分开的划分超平面可能有很多,我们要寻找的是最优超平面(粗实线),最优超平面对训练样本扰动容忍性好(如果出现更接近分类间隔的样本点,出错的概率小很多,即泛化性能好)。
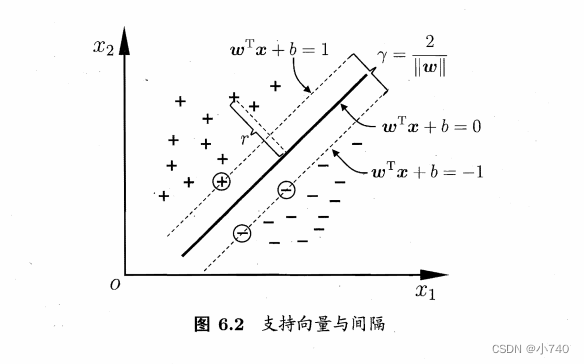
如图6.2,距离超平面最近的几个训练样本使得等号成立:
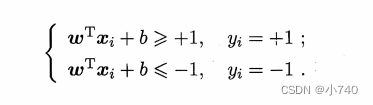
使得等式成立的样本点被称为“
支持向量
”,“+”类和“-”类的两个支持向量到超平面的距离之和为:
γ =
2
∣
∣
w
∣
∣
\frac{2} {||w||}
∣∣
w
∣∣
2
γ被称为间隔。
“
最大间隔
”的划分超平面:寻找满足式中约束的参数
w
和
b
,使得
λ
最大。
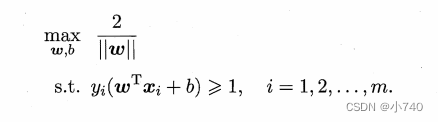
最大化间隔
λ
*(
2
∣
∣
w
∣
∣
\frac{2}{||w||}
∣∣
w
∣∣
2
)仅需最大化||w||
-1
,等价于最小化||w||
2
.于是,可重写出支持向量机(SVM)的基本型,即:
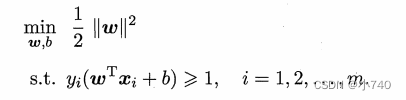
二、术语及符号解释
对偶问题
:任何一个求极大化的线性规划问题都有一个求极小化的线性规划问题与之对应,反之亦然,如果我们把其中一个叫原问题,则另一个就叫做它的对偶问题,并称这一对互相联系的两个问题为一对对偶问题。
鲁棒性
:机器学习中,常用于形容算法模型,当说算法模型具有鲁棒性时,表明对这个算法模型而言,一些
异常的数据对整体的性能影响不大或者基本没有影响
。
泛化能力
:算法模型
对未知数据的预测能力。
KKT条件
:判断==x*==是否为最优解的必要条件。
升维
:对于分类问题,有时原始样本空间内不存在一个正确划分两类样本的超平面,如果将原始空间映射到更高维的特征空间,会更容易划分(
原始空间有限维,即属性数有限,必然线性可分
)。
核技巧
:对于高维特征空间,位数很高,带来计算量复杂,甚至无法计算。将高维空间特征的计算结果 通过函数 κ(x
i
, x
j
)计算原始空间的属性来得到的技巧。对应的κ(x
i
, x
j
)是
核函数
;
希尔伯特空间
:完备的内积空间,定义了加法和数乘,距离,内积,具有完备性的空间。希尔伯特空间中的元素一般是函数,因为一个函数可以视为一个无穷维的向量。
“再生核希尔伯特空间”
(Reproducing Kernel Hilbert Space,简称 RKHS):我们定义了一种核函数(例如径向基函数),就定义了一个希尔伯特空间,而这个核函数的再生性使得我们可以不去计算高维特征空间中的內积,而只需计算核函数,降低了大量的计算量。
软间隔
:允许支持向量机在一些样本上出错。
三、公式推导

四、反思
对偶问题、软间隔、支持向量回归等公式推导还不是很清楚,比较模糊,后期需要留意这方面知识的学习。
参考文献:
浅谈最优化问题的KKT条件
一片文章带你理解再生核希尔伯特空间(RKHS)以及各种空间
周志华.机器学习[M].北京:清华大学出版社,2016.01
谢文睿 / 秦州. 机器学习公式详解. 北京:人民邮电出版社,2021.03.