1. 堆的概念
堆的数据结构也即是个顺序存储的完全二叉树
。在STL容器当中的实现为
p
r
i
o
r
i
t
y
_
q
u
e
u
e
priority\_queue
p
r
i
o
r
i
t
y
_
q
u
e
u
e
,即优先队列。
之前左神的视频中已经讲过,昨日腾讯音乐一面要求写堆排序,时间比较久远且当时的代码也比较复杂。因此,在这里重新整理一下。之前的实现方法见:
排序归纳总结(插入排序、归并排序、堆排序、快速排序、桶排序)——3. 堆排序
。
其中每个结点的关键字都不大于其孩子结点的关键字,这样的堆称为
小根堆
。
其中每个结点的关键字都不小于其孩子结点的关键字,这样的堆称为
大根堆
。
2. 堆的实例
举例来说,对于
n
n
n
个元素的序列
n
u
m
s
0
,
n
u
m
s
1
,
.
.
.
,
n
u
m
s
n
{nums_0, nums_1, … , nums_n}
n
u
m
s
0
,
n
u
m
s
1
,
.
.
.
,
n
u
m
s
n
当且仅当满足下列关系之一时,称之为堆:
(1)
n
u
m
s
i
<
=
n
u
m
2
i
+
1
nums_i <= num_{2i+1}
n
u
m
s
i
<
=
n
u
m
2
i
+
1
且
n
u
m
s
i
<
=
n
u
m
2
i
+
2
nums_i <= num_{2i+2}
n
u
m
s
i
<
=
n
u
m
2
i
+
2
(小根堆)
(2)
n
u
m
s
i
>
=
n
u
m
2
i
+
1
nums_i >= num_{2i+1}
n
u
m
s
i
>
=
n
u
m
2
i
+
1
且
n
u
m
s
i
>
=
n
u
m
2
i
+
2
nums_i >= num_{2i+2}
n
u
m
s
i
>
=
n
u
m
2
i
+
2
(大根堆)
其中
i
=
1
,
2
,
…
,
n
2
i=1,2,…,\frac{n}{2}
i
=
1
,
2
,
…
,
2
n
向下取整;

如上图所示,
序列
n
u
m
s
{
3
,
8
,
15
,
31
,
25
}
nums\{3, 8, 15, 31, 25\}
n
u
m
s
{
3
,
8
,
1
5
,
3
1
,
2
5
}
是一个典型的小根堆。
堆中有两个父结点(
n
u
m
s
.
s
i
z
e
(
)
>
>
1
=
f
l
o
o
r
(
5
2
)
=
2
nums.size() >> 1 = floor(\frac{5}{2}) = 2
n
u
m
s
.
s
i
z
e
(
)
>
>
1
=
f
l
o
o
r
(
2
5
)
=
2
,这里父节点的个数可以理解为子树的个数),元素
3
3
3
和元素
8
8
8
。
元素
3
3
3
在数组中以
n
u
m
s
[
0
]
nums[0]
n
u
m
s
[
0
]
表示,它的左孩子结点是
n
u
m
s
[
1
]
nums[1]
n
u
m
s
[
1
]
,右孩子结点是
n
u
m
s
[
2
]
nums[2]
n
u
m
s
[
2
]
。
元素
8
8
8
在数组中以
n
u
m
s
[
1
]
nums[1]
n
u
m
s
[
1
]
表示,它的左孩子结点是
n
u
m
s
[
3
]
nums[3]
n
u
m
s
[
3
]
,右孩子结点是
n
u
m
s
[
4
]
nums[4]
n
u
m
s
[
4
]
,它的父结点是
n
u
m
s
[
0
]
nums[0]
n
u
m
s
[
0
]
。
可以看出,它们满足以下规律:
设当前元素在数组中以
n
u
m
s
[
i
]
nums[i]
n
u
m
s
[
i
]
表示,那么:
-
(1) 它的
左孩子结点是:
nu
m
s
[
2
i
+
1
]
nums[2i+1]
n
u
m
s
[
2
i
+
1
]
;
-
(2) 它的
右孩子结点是:
nu
m
s
[
2
i
+
2
]
nums[2i+2]
n
u
m
s
[
2
i
+
2
]
;
-
(3) 它的
父结点是:
nu
m
s
[
i
−
1
2
]
nums[\frac{i-1}{2}]
n
u
m
s
[
2
i
−
1
]
;
-
(4)
nu
m
s
[
i
]
<
=
n
u
m
s
[
2
i
+
1
]
nums[i] <= nums[2i+1]
n
u
m
s
[
i
]
<
=
n
u
m
s
[
2
i
+
1
]
且
nu
m
s
[
i
]
<
=
n
u
m
s
[
2
i
+
2
]
nums[i] <= nums[2i+2]
n
u
m
s
[
i
]
<
=
n
u
m
s
[
2
i
+
2
]
(小根堆特征)。
3. 堆排过程
3.1 堆排思想
堆排序基本思想:
将待排序序列(元素数目为
n
n
n
)构造为一个大/小顶堆,此时,整个序列的最大/小值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大/小值。然后将剩余
n
−
1
n-1
n
−
1
个元素重新构造成一个堆,这样会得到
n
n
n
个元素的次小值。如此反复执行,便可得到一有序序列了。
具体操作层面上为:
-
(1) 根据初始数组去构造初始堆(构建一个完全二叉树,保证所有的父结点都比它的孩子结点数值大/小,
构建过程只需从非叶子节点进行逆序调整即可,次第对父节点沿着深搜路径(从根节点到叶子节点)进行顺序调整
); - (2) 每次交换第一个和最后一个元素,输出最后一个元素(最大/小值),然后把剩下元素重新调整为大/小根堆;
3.2 堆排过程示意
以无序序列
{
1
,
3
,
4
,
5
,
2
,
6
,
9
,
7
,
8
,
0
}
\{ 1, 3, 4, 5, 2, 6, 9, 7, 8, 0 \}
{
1
,
3
,
4
,
5
,
2
,
6
,
9
,
7
,
8
,
0
}
的升序排序为例:
(1) 构建初始大根堆:
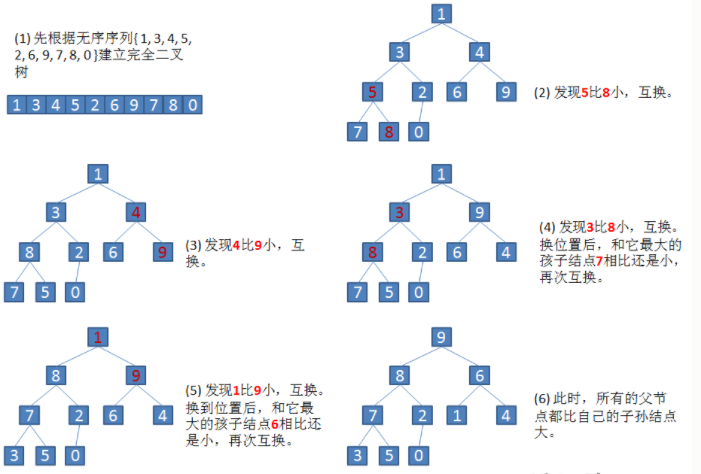
(2) 取出最大值放置到序列末尾,除开序列末尾将剩余元素重新调整为大根堆,重复该操作直至剩余元素的个数为1:

3.3 堆排代码实现
代码实现,使用LeetCode中的
912. 排序数组
进行测试,这里所求的是升序序列,也即是大根堆实现对无序数组的排序,实现的代码如下:
class Solution {
public:
vector<int> sortArray(vector<int>& nums) {
//由完全二叉树性质,从非叶子节点/内部节点进行逆序遍历,
//右边界下标为nums.size() >> 1;
//构建初始的大根堆数据结构
for(int i = nums.size() >> 1; i >= 0; --i)
heapAdjust(nums, i, nums.size());
//进行首尾元素交换,并重新调整数组元素位置确保剩余元素是大根堆结构
for(int i = nums.size() - 1; i > 0; --i) {
//首位元素交换
int tmp = nums[i];
nums[i] = nums[0];
nums[0] = tmp;
//调整剩余元素为大根堆
heapAdjust(nums, 0, i);
}
return nums;
}
private:
void heapAdjust(vector<int>& nums, int parent, int size) {
int tmp = nums[parent]; //记录父节点数值
int child = parent * 2 + 1; //左节点的下标
while(child < size) { //当未到达叶子节点
//更新child下标,使其等于parent的左右子节点的较大的节点下标
child = child + 1 < size && nums[child] < nums[child+1] ? child + 1 : child;
//如果父节点数值大于子节点较大值下标,满足大根堆,跳出
if(tmp >= nums[child]) break;
//如果小于,则不满足,进行替换,并继续按照最大子节点的路径进行下沉操作,
//直至找到父节点数值的合适位置,最终合适位置是parent下标;
nums[parent] = nums[child];
parent = child; //更新parent
child = child * 2 + 1; //更新左节点下标
}
//可理解为环形数组的移位过程,可以注意到上图构建初始化大根堆中的第(4)图,
//{3, 8, 7}路径替换为了{8, 7, 3}
nums[parent] = tmp;
}
};
4. 复杂度分析
总体情况如下:

时间复杂度:
堆排序是一种选择排序,整体主要由构建初始堆+交换堆顶元素和末尾元素并重建堆两部分组成。
其中构建初始堆经推导复杂度为
O
(
n
)
O(n)
O
(
n
)
,在交换并重建堆的过程中,需交换
n
−
1
n-1
n
−
1
次,而重建堆的过程中,根据完全二叉树的性质,
[
l
o
g
2
(
n
−
1
)
,
l
o
g
2
(
n
−
2
)
.
.
.
1
]
[log_2(n-1),log_2(n-2)…1]
[
l
o
g
2
(
n
−
1
)
,
l
o
g
2
(
n
−
2
)
.
.
.
1
]
逐步递减,近似为
n
l
o
g
n
nlogn
n
l
o
g
n
。所以堆排序时间复杂度一般认为就是
O
(
n
l
o
g
n
)
O(nlogn)
O
(
n
l
o
g
n
)
级。


- 堆的存储表示是顺序的。因为堆所对应的二叉树为完全二叉树,而完全二叉树通常采用顺序存储方式;
-
当想得到一个序列中第
kk
k
个最小的元素之前的部分排序序列,最好采用堆排序,堆排序的
时间复杂度是
O(
n
+
k
l
o
g
2
n
)
O(n+klog_2n)
O
(
n
+
k
l
o
g
2
n
)
,若
k≤
n
l
o
g
2
n
k≤\frac{n}{log_2n}
k
≤
l
o
g
2
n
n
,则可得到的时间复杂度为
O(
n
)
O(n)
O
(
n
)
;
算法稳定性:
堆排序是一种
不稳定
的排序方法。因为在堆的调整过程中,关键字进行比较和交换所走的是该结点到叶子结点的一条路径,因此对于相同的关键字就可能出现排在后面的关键字被交换到前面来的情况。