写在开头:实验结果截图8皇后太多截不完,用4皇后代替了,只需将n->8就行
目录
图解算法过程:

下面分析中的
(
x
,
y
)
(x,y)
(
x
,
y
)
相当于上面的
(
u
,
i
)
(u,i)
(
u
,
i
)
反对角线
y
=
x
+
b
y=x+b
y
=
x
+
b
, 截距
b
=
y
−
x
b=y−x
b
=
y
−
x
,因为我们要把
b
b
b
当做数组下标来用,显然
b
b
b
不能是
负
的,所以我们
加上 n
(实际上
+
n
+
4
+n+4
+
n
+
4
,
+
2
n
+2n
+
2
n
都行),来保证是结果是正的,即
y
−
x
+
n
y – x + n
y
−
x
+
n
而对角线
y
=
−
x
+
b
y=−x+b
y
=
−
x
+
b
截距是
b
=
y
+
x
b=y+x
b
=
y
+
x
,这里截距一定是
正
的,所以
不需要加偏移量
核心目的:找一些合法的下标来表示
dg
或
udg
是否被标记过,所以如果你愿意,你取
udg[n−u+i]
也可以,只要所有
(u,i)
对可以映射过去就行
算法一:DFS 按行枚举,时间复杂度O(n!)
const int N=25;
int n;
char g[N][N];
bool dg[N],udg[N],col[N];//对角线 dg[u+i],反对角线udg[n−u+i]中的下标 u+i和 n−u+i 表示的是截距
int k=1;
void dfs(int u)
{
if(u==n)
{
cout<<n<<"皇后的第"<<k++<<"种方案:"<<endl;
for(int i=0;i<n;i++)
cout<<g[i]<<endl;
cout<<endl;
return;
}
for(int i=0;i<n;i++)
{
if(!col[i]&&!dg[u+i]&&!udg[n-u+i])
{
g[u][i]='Q';
col[i]=dg[u+i]=udg[n-u+i]=true;//标记
dfs(u+1);
col[i]=dg[u+i]=udg[n-u+i]=false;//还原现场
g[u][i]='.';
}
}
}
void solve()
{
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
g[i][j]='.';
dfs(0);
}
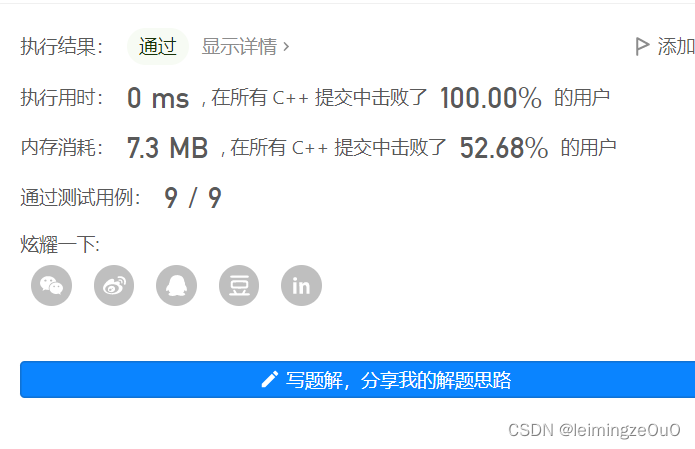
运行结果截图:

算法二:DFS按每个元素枚举 时间复杂度
O
(
2
n
2
)
O(2^{n^2})
O
(
2
n
2
)
,每个位置都有两种情况,总共有
n
2
n^2
n
2
个位置
const int N=25;
int n;
char g[N][N];
bool dg[N],udg[N],col[N],row[N];
int k=1;
void dfs(int x,int y,int s)
{
if(y==n)y=0,x++;
if(x==n)
{
if(s==n)
{
cout<<n<<"皇后的第"<<k++<<"种方案:"<<endl;
for(int i=0;i<n;i++)
cout<<g[i]<<endl;
cout<<endl;
}
return;
}
if(!row[x]&&!col[y]&&!dg[x+y]&&!udg[x-y+n])//选
{
g[x][y]='Q';
row[x]=col[y]=dg[x+y]=udg[x-y+n]=true;
dfs(x,y+1,s+1);
row[x]=col[y]=dg[x+y]=udg[x-y+n]=false;
g[x][y]='.';
}
//不选
dfs(x,y+1,s);
}
void solve()
{
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
g[i][j]='.';
dfs(0,0,0);
}
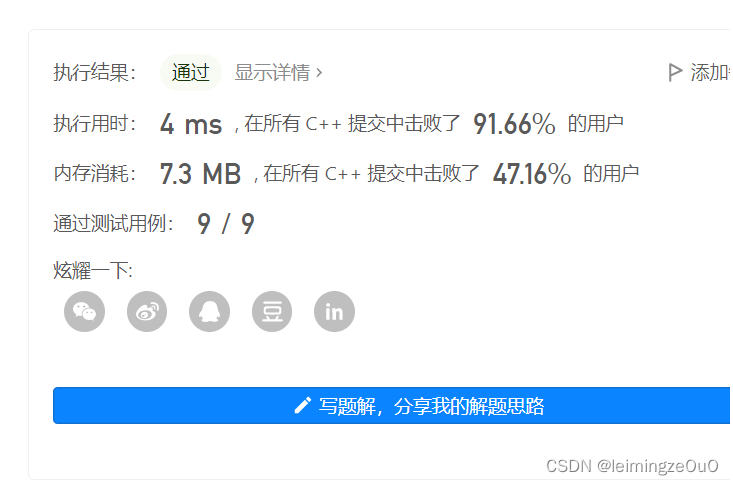
运行结果截图

算法三:二进制对空间进行优化
int lowbit(int x){return x&-x;}//最低位1及其后面的0构成的数值
const int N=25;
int n;
vector<string>g;
vector<vector<string>>res;
int cnt=1;
void dfs(int a,int b,int c,int k)
{
if(k==n)
{
res.push_back(g);
return;
}
for(int i=~(a|b|c)&((1<<n)-1);i;i-=lowbit(i))
{
int p=lowbit(i);
g[k][log2(p)]='Q';//计算第几位是1,用对数函数log2十分方便
dfs((a|p)<<1,(b|p)>>1,c|p,k+1);
g[k][log2(p)]='.';
}
}
void solve()
{
cin>>n;
vector<string>board(n,string(n,'.'));
g=board;
dfs(0,0,0,0);
for(int i=0;i<res.size();i++)
{
cout<<n<<"皇后的第"<<cnt++<<"种方案:"<<endl;
for(int j=0;j<res[i].size();j++)
{
cout<<res[i][j]<<endl;
}
cout<<endl;
}
}
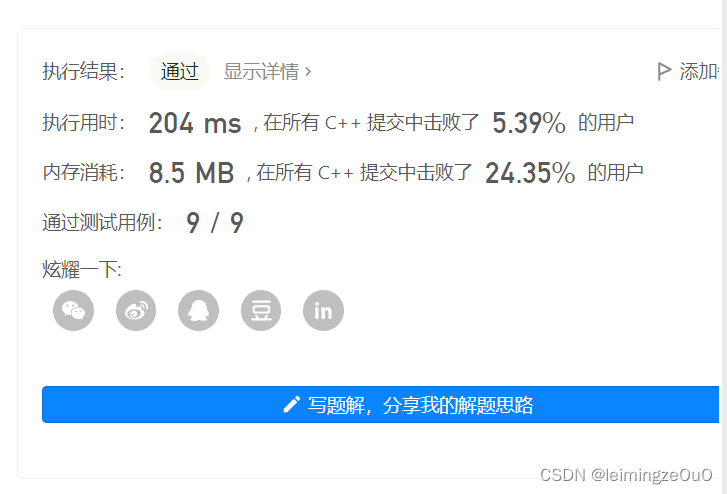
运行结果截图