凝聚法分层聚类中有一堆方法可以用来算两点(pair)之间的距离:欧式,欧式平方,manhattan等,还有一堆方法可以算类(cluster)与类之间的距离,什么single-linkage、complete-linkage、还有这个ward linkage。(即最短最长平均,离差平方和)
其他的好像都挺好理解,就是最后这个有点麻烦。。。
这个方法说白了叫离差平方和(这是个啥?)。是ward写那篇文章时候举的一个特例。这篇文章是说分层凝聚聚类方法的一个通用流程。在选择合并类与类时基于一个object function optimise value,这个object function可以是任何反应研究目的的方程,所以许多标准的方法也被归入了。为了阐明这个过程,ward举了一个例子,用的object function 是error sum of squares(ESS),这个例子就成为ward’s method。
找了N多资料,终于把这个算法的过程搞清楚了。首先输入的是一个距离矩阵,知道每两个点之间的距离。然后初始化是每个点做为一个cluster,假设总共N组,此时每个组内的ESS都是0,ESS的公式,如下(从原稿《Hierarchical Grouping To Optimize An Objective Function》上摘的):
我当时还有点蒙ESS是个啥?——我现在知道了,凡是蒙的都是概率没学好(我是说我)……先从wiki上转个公式过来:
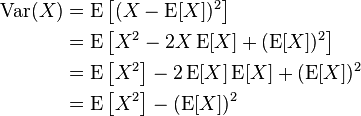
这是方差的公式,写的再通俗点,就是:
等号两边同时乘上n,好了,你应该知道ESS是啥了——ESS就是【方差×n】!so easy了~~
但是等下——这看起来是个一维的公式啊——因为你已经知道ESS是【方差×n】了,那多维的还不会算吗?先求所有点的均值点
,然后再算所有点到这个均值点(central)的距离(距离公式你得自己定,见开头,但是最后算出来就是一个数),然后把所有距离平方后加起来(此时即为方差乘上n),就得到ESS了。
说了半天光说ESS了,列位看官,人只有一张嘴,故ESS此处按下不表,接着说ward method。ward method是要求每次合并后ESS的增量最小,这怎么讲呢?还是上图吧(图是从youtube上的一个教程里截的):

只看最下面ward’s method的两个图好了,先看下面的图,合并前红色组和黄色组分别能算各自的ESS,总的ESS是什么呢?很简单,加起来就好了,即:
ESS(总-合并前)=ESS(红)+ESS(黄)+ESS(其他没画出来的组)
如果合并这两个组,则可以作为一个新组再算一个ESS,此时
ESS(总-合并后)=ESS(红黄)+ESS(其他没画出来的组)
你注意这里还没有真的合并,只是算了一下合并红黄两组的“成本”(即:ESS(总-合并后)-ESS(总-合并前),当然这个成本肯定是增加的),如果总共有N个组,必须把每两个组合并的成本都算一遍,也就是算N×(N-1)/2个数出来,然后找里面合并后成本最小的两组合并。然后再重复这个过程。
我说清楚了吧!?
嗯,至于画的那个树状图的高度,可以认为是上面说的这个“成本”。
对了,还得说一下这个公式:
啥意思呢,就是说,如果用ward’s method来度量两个cluster之间的距离,那么两个cluster之间的距离就是把这两个cluster合并后新cluster的ESS,其中x就表示合并前两个cluster中所有点,而
就是合并后那个新cluster的中心点(均值点),
就表示每个点x到中心点的距离,平方后加起来,就是ESS了。
好了,总结一下,ward’s method是凝聚法分层聚类中一种度量cluster之间距离的方法。按照这个方法,任意两个cluster之间的距离就是这两个cluster合并后新cluster的ESS
摘要: ward linkage method是什么不介绍了,只说下怎么算,有一个快速的计算方法叫Lance-Williams Algorithm可以大大简化ward method的计算
ward’s method是分层聚类凝聚法的一种常见的度量cluster之间距离的方法,其基本过程是这样的(参考:http://blog.sciencenet.cn/blog-2827057-921772.html )
计算每个cluster的ESS
计算总的ESS
枚举所有二项cluster【N个cluster是N*(N-1)/2个二项集】,计算合并这两个cluster后的总ESS值
选择总ESS值增长最小的那两个cluster合并
重复以上过程直到N减少到1
这个方法其实效率比较低,特别是算cluster的ESS值还要先求均值点,然后算距离的平方再求和,不过有一个快速的计算方法叫Lance-Williams Algorithm可以大大简化ward method的计算。先来一个图(来源:https://www.youtube.com/watch?v=aXsaFNVzzfI

然后你其实可以发现,这个算法简化的是合并后更新ESS的那部分过程,比如有ABCDE五个cluster,合并了AB,那么后面要更新CDE到这个AB的距离,怎么算?ESS呗——平方和——好复杂!
那用这个新算法怎么算?答,新算法可以不用ESS的公式计算ESS,直接套用上面那个公式(注意最后绝对值里面应该一个i一个j,他写错了)。初始的ESS由两点之间的距离决定——所以就是说完全不需要算ESS了!
好了,试着写一下算法:输入是一个距离矩阵,输出是一个合并序列[(cluster1id, cluster2id, distance), …]
clusterDistance=dict() #存放cluster之间的距离,形如’1-2′:3表示cluster1与cluster2之间的距离为3
clusterMap=dict() #存放cluster的情况,形如’1′:4表示cluster1里面有4个元素(样本)
clusterCount=0 #每合并一次生成新的序号来命名cluster
defward_linkage_method(distance_matrix):
N=len(distance_matrix)
clusterCount=N-1
for i in range(0,N-1):
for j in range(i,N):
name=getName(i,j)
clusterDistance[name]=distance_matrix[i][j]
for k in range(0,N):
clusterMap[k]=1
while True:
# 查找距离最短的两个cluster
# clusterDistance里面有冗余(即合并后之前的距离仍在,
# 所以循环以clusterMap为准,这个里面没有冗余。
tmp=max(clusterDistance.values())
clusterList = clusterMap.keys()
clusterListLength=len(clusterList)
for iii in range(0, clusterListLength-1):
for jjj in range(iii+1, clusterListLength):
name=getName(clusterList[iii], clusterList[jjj])
if tmp > clusterDistance[name]:
i=iii
j=jjj
tmp=clusterDistance[name]
ni=clusterMap[i] # 第i个cluster内的元素数
nj=clusterMap[j]
del clusterMap[i] # 删掉原来的cluster
del clusterMap[j]
clusterCount+=1 # 新增新的cluster
clusterMap[clusterCount]=ni+nj #新cluster的元素数是之前的总和
print i,j,’->’,clusterCount,tmp # 输出合并信息:i,j合并为clusterCount,合并高度(距离)为tmp
if len(clusterMap)==1:break # 合并到只剩一个集合为止,然后退出
# 更新没合并的cluster到新合并后的cluster的距离
for k in clusterMap.keys():
if k==clusterCount:continue
else: # 计算新的距离
nk=clusterMap[k]
alpha_i=(ni+nk)/(ni+nj+nk)
alpha_j=(nj+nk)/(ni+nj+nk)
beta= -nk/(ni+nj+nk)
newDistance = alpha_i * clusterDistance[getName(i,k)]
newDistance += alpha_j * clusterDistance[getName(j,k)]
newDistance += beta * clusterDistance[getName(i,j)]
# 把新的距离加入距离集合
clusterDistance[getName(clusterCount,k,’.’)]=newDistance
defgetName(i,j):
t=[i,j]
t.sort()
return t[0]+’-‘+t[1]
当然了,这段代码只是一个示意,可以改进的地方还很多。
转载本文请联系原作者获取授权,同时请注明本文来自宋景和科学网博客。
链接地址:http://blog.sciencenet.cn/blog-2827057-921772.html