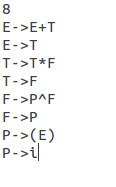概念简述
移动归约分析法:
自底向上的语法分析方法,也称为
移动归约分析法
。
-
最易于实现的一种移动归约分析方法,叫做
算符优先分析法
, -
而更一般的移动归约分析方法叫做
LR分析法
,LR分析法可以用作许多自动的语法分析器的生成器。
短语:
文法G[S],αβδ是文法G的一个句型,S=>*αAδ且A=>+β则称β是句型αβδ相对于非终结符A的短语。
直接短语:
若有A
⇒
+
β则称β是句型αβδ相对于该规则A→β的直接短语。
句柄:
一个句型的最左直接短语称为该句型的句柄。
树定义方法更容易理解….
短语:
一棵子树的所有叶子自左至右排列起来形成一个相对于子树根的短语。
直接短语:
仅有父子两代的一棵子树,它的所有叶子自左至右排列起来所形成的符号串。
句柄:
一个句型的分析树中最左那棵只有父子两代的子树的所有叶子的自左至右排列。
算符文法的定义:
- 所有产生式的右部都不是ε或两个相邻的非终结符
- 设有一个文法G,如果G中没有形如A→…BC…的产生式,其中B和C为非终结符,则称G为算符文法(Operator Grammar)也称OG文法.
算符优先文法的特点:
- 一旦我们构造了算符优先语法分析器,就可以忽略原来的文法,栈中的非终结符仅仅作为与这些非终结符相关的属性的占位符
- 难以处理像减号这样有不同优先级的符号
- 由于分析的语言的文法和算符优先语法分析器本身的关系不是很紧密,所以不能肯定语法分析器接受的就是所期望的语言
算法优先关系构造算法
一、首先对于优先关系进行如下定义:
-
a的优先级低于b
a < b:
文法中有形如A→…aB…的产生式而B+b…或B+Cb… -
a的优先级等于b
a = b:
文法中有形如A→…ab…或者A→…aBb…的产生式 -
a的优先级高于b
a > b:
文法中有形如A…Bb…的产生式,而B+…a或B+…aC -
算符的优先关系是有序的
- 如果a > b,不能推出b < a
- 如果a > b,有可能b > a
-
如果a > b, b > c,不一定a > c
根据这个大小关系的定义,我们知道为了确定两个终止符的优先关系,我们需要知道它的在所有的产生式中和前后非终止符的关系,那么我们做一个如(二)预处理:
二、定义并构造FIRSTVT和LASTVT两个集合
F
I
R
S
T
V
T
(
P
)
=
{
a
|
P
⇒
+
a
⋯
或
P
⇒
+
Q
a
⋯
}
L
A
S
T
V
T
(
P
)
=
{
a
|
P
⇒
+
⋯
a
或
P
⇒
+
⋯
a
Q
}
FIRSTVT(P)直接根据定义递归的构造即可:
-
a) 若有产生式 P→a••• 或 p→Qa•••
则 a∈FIRSTVT(P) -
b) 若有产生式 P→Q••• ,
若 a∈FIRSTVT(Q)
则 a∈FIRSTVT(P)
LASTVT(P)直接根据定义递归的构造即可:
-
a) 若有产生式 P→•••a 或 p→•••aQ
则 a∈LASTVT(P) -
b) 若有产生式 P→•••Q ,
若 a∈LASTVT(Q)
则 a∈LASTVT(P)
代码实现见代码部分的make_first和make_last函数,是两个简单的递归实现。
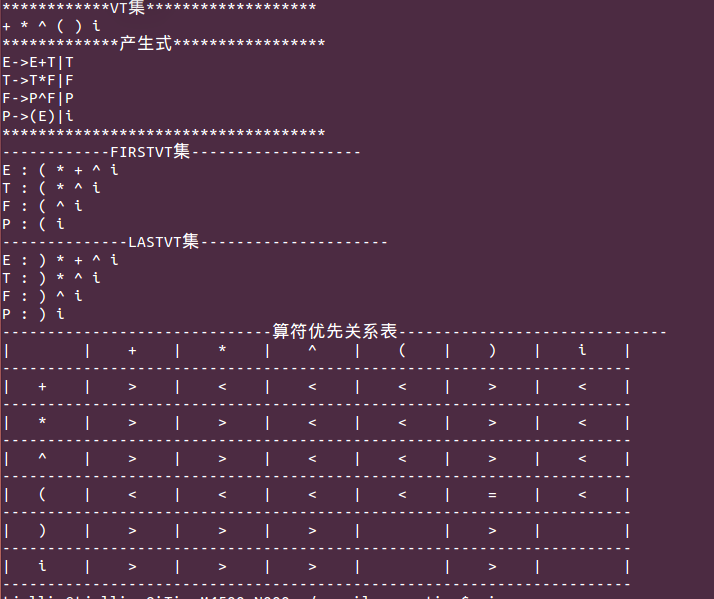
三、利用FIRSTVT和LASTVT集合构造算法优先关系表
FOR 每个产生式 P->X1 X2 ……Xn
DO FOR i:=1 TO n-1 DO
IF X[i]和X[i+1]均为终结符
THEN 置 X[i]=X[i+1]
IF X[i]和X[i+2]均为终结符,X[i+1]为非终结符,i≤n-2,
THEN 置 X[i]=X[i+2]
IF X[i]为终结符, 但X[i+1]为非终结符
THEN FOR FIRSTVT(X[i+1])中的每个a
DO 置 X[i]<a
IF X[i]为非终结符, 但X[i+1]为终结符
THEN FOR LASTVT(X[i])中的每个a
DO 置 a>X[i+1]
Input:
Output:
————————————————————————————————————————————————————————————–
素短语的概念
:
它是一个递归的定义,
至
少含有一个终结符
,并且除它自身之外不再含任何更小的素短语
,所谓最左素短语就是处于句型最左边的素短语的短语。而一个算符优先文法G的任何句型的最左素短语是满足以下条件的最左子串NaNb…NcNdN(N是非终结符,a,b,c,d是终结符)
实例:句型T+T*F+id,求出其语法树,可知,T*F是最左素短语,id也是素短语,但不是最左的。
短语和直接短语的概念
:
一个句型的语法树中
任
一子树叶结点所组成的符号串
都是该句型的短语,当子树中不包含其他更小的子树时,该子数叶结点所组成的字符串就是该句型的直接(简单)短语。
句柄的概念
:
一个句型的
最左直接短语
汇称为该句型的句柄
例子1:
E->T|E+T
T->F|T*F
F-> (E) | i
给出句型T*F+i的最右推导。
1.首先通过最右推导(也叫规范推导):
E=>E+T=>E+F=>E+i=>T+i=>T*F+i
2.画出语法树
E
/ | \
E + T
|
|
T
F
/
| \ |
T * F i
因此本题的直接短语的为 T*F、i,短语有T*F+i, T*F, i。句柄是T*F.
+号不是直接短语,因为+所在的树中那个E,T结点还推出来一颗子树,所以它不是。
例子2
S
->
a|b|(T)
T -> TdS|S
题目中的句型可用下面的语法树表示:
S
/
|
\
(
T
)
/ |
\
T
d
S
/ | \
|
T
d
S
b
|
/ | \
S
(
T
)
因此本题的直接短语的为
S
、(T)、b
,短语有
S、(T)、b、Sd(T)、Sd(T)db
、(Sd(T)db)
。
d不是直接短语,因为d所在的树中那个T结点还推出来一颗子树,所以它不是。
素语是一个短语,它至少含有一个终结符,而且除它自身以外不再含有更少的素短语,对于句型(Sd(T)db)的素短语是(T)、b.
除了画语法树,还可以通过直接推导的结果,不过个人觉得很容易出错,我们还是画语法树吧。
收集了一些总结,方便查询。
每个句型对应一棵语法树
每棵语法树的叶子结点从左到右排列构成一个句型
每棵语法树的
子树的叶子结点从左到右
排列构成一个短语
每棵语法树的简单子树(只有父子两层结点)的叶子结点从左到右排列构成一个简单(直接)短语
每棵语法树的最左简单子树(只有父子两层结点)的叶子结点从左到右排列构成句柄
素短语是
至少包含一个终结符
的短语,但它不能包含其它素短语
最左推导:在每个推导过程中,总是首先考虑对当前最左边的非终结符号进行推导
最右推导:在每个推导过程中,总是首先考虑对当前最右边的非终结符号进行推导