用matlab可以做出二维正态分布密度函数的图像。本文简单介绍二维正态分布及其性质,并给出用matlab的做图程序。
很多现象服从二维正态分布。例如某年龄段小女孩的身高和腿长,某种昆虫的触角长和翼长,成年男子的身高和体重等等。
二维正态分布概率密度函数的解析式为:
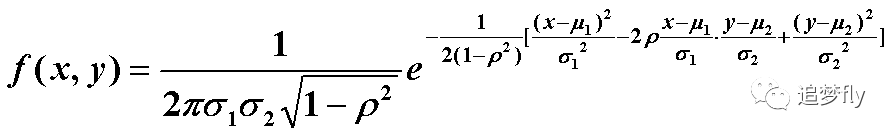
有的地方记为
显然,二维正态分布有5个参数。
二维正态分布的边缘分布是一维正态分布。其中
最后一个参数r表示的是X与Y的相关系数。
如果(X,Y)服从二维正态分布,则X、Y不相关和X、Y独立等价。但是特别注意:若X与Y不独立,则(X,Y)不一定服从二维正态分布,即便r=0的时候。
用matlab做二维正态分布密度函数图像的程序如下:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
u=[1,2];d=[1,2];r=0.3;%给出5个参数值,u是期望向量,d是标准差向量,r是相关系数x=u(1)-3*d(1):0.05:u(1)+3*d(1);%给出x的三倍标准差范围y=u(2)-3*d(2):0.05:u(2)+3*d(2);%给出y的三倍标准差范围[X,Y]=meshgrid(x,y);%生成以x为行,y为列的矩阵part1=(2*pi*d(1)*d(2)*sqrt(1-r^2))^(-1);part2=-1/(2*(1-r^2));partx=(X-u(1)).^2./d(1)^2;party=(Y-u(2)).^2./d(2)^2;partxy=2*r.*(X-u(1)).*(Y-u(2))./(d(1)*d(2));z=part1*exp(part2*(partx-partxy+party));%计算密度函数值mesh(X,Y,z)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
运行结果:
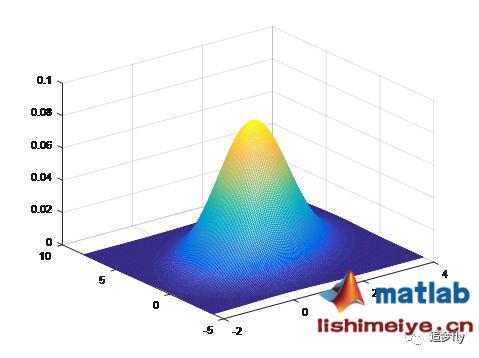
一般的n维正态分布的定义为:

二维正态分布也可以写成一般正态分布的形式。其中协方差矩阵为:
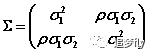
协方差矩阵的行列式:
协方差矩阵的逆矩阵:
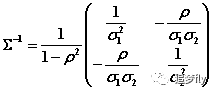
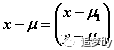
代入n维正态分布密度函数的一般式即可得二维正态分布密度函数解析式。