博客

前言

算法分析——分治法

一、已知前序和中序构造二叉树，并层次输出

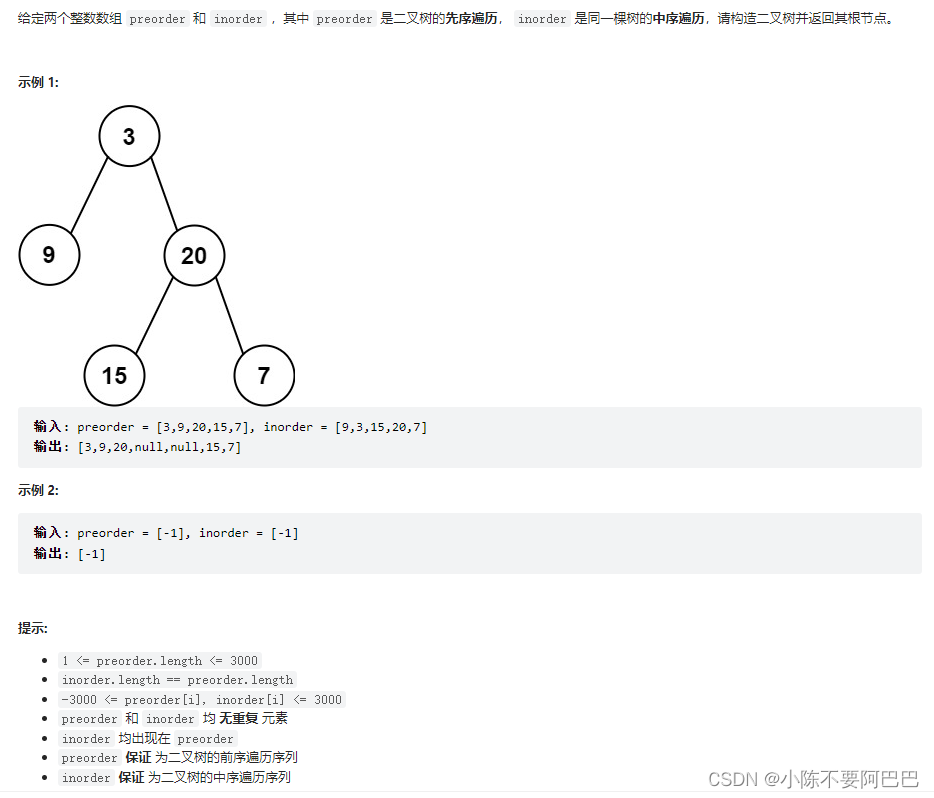
二、问题分析

首先我们获取到的信息为一个

前序遍历

的数组和一个

中序遍历

的数组。前序遍历的顺序为

根左右

，中序遍历的顺序为

左根右

。

1.构造二叉树

我们首先应该找到树的

根节点

，也就是前序遍历的第一个数，并在中序遍历中标记出根节点的位置，随后便可知道左子树和右子树的节点个数

		// 根节点值是前序遍历的第一个
		TreeNode root = new TreeNode(preorder[pleft]);
		// 中序遍历第一个为起始点
		int middle = ileft;
		// 左子树节点长度
		int len = 0;
		// 找到中序遍历中的根节点位置记为middle
		for (; middle < inorder.length; middle++) {
			if (inorder[middle] == preorder[pleft]) {
				break;
			}
			// 计算左子树节点长度len
			len++;

随后我们就可以通过递归调用求解出左右子树


提示：



[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]



[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]


		// 递归调用求解左右子树
		// 左子树：前序遍历为根后一个到根加左子树长度，中序遍历为第一个到根节点位置前一个
		root.left = buildtree(preorder, pleft + 1, pleft + len, inorder, ileft, middle - 1);
		// 右子树：前序遍历为左子树后一个到最后一个，中序为根节点后一个到最后一个
		root.right = buildtree(preorder, pleft + len + 1, pright, inorder, middle + 1, iright);

这样，我们就通过递归的方法成功构建出了一颗二叉树。这时我们就应当考虑如何通过层次遍历输出这颗二叉树。

2.层次遍历二叉树

我们通过层次遍历二叉树的时候，需要用到

队列

的数据结构。利用队列先进先出的原则，将二叉树元素依次存进List集合中

1. 先将二叉树的根节点通过**offer()**方法添加进队尾。
   
   
   ¹
   
   
2. 队列非空时，将队列中的头元素取出，并将值存进 List 集合中
3. 当这个头元素对应的左子节点非空时，将该左子节点添加进队列；右子节点同理
4. 当队列为空时，循环结束

			// 定义一个队列用于层次遍历二叉树
			Queue<BuildTree1.TreeNode> queue = new LinkedList<>();
			queue.offer(root);// offer方法表示添加元素到队尾
			while (!queue.isEmpty()) {
				BuildTree1.TreeNode temp = queue.poll();// poll方法删除队头元素
				result.add(temp.val);
				if (temp.left != null) {
					queue.offer(temp.left);
				}
				if (temp.right != null) {
					queue.offer(temp.right);
				}
			}

三、总结

这道题目比较简单，应熟悉掌握树的数据结构逻辑


代码及运行结果：


package day1;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Scanner;

public class BuildTree1 {
	public static class TreeNode {
		int val;
		TreeNode left;
		TreeNode right;
		TreeNode(int x) {
			val = x;
		}
	}

	// 传入前序和中序遍历
	public static TreeNode buildTree(int[] preorder, int[] inorder) {
		if (preorder == null || inorder == null) {
			return null;
		}
		// 非空，则开始还原二叉树
		return buildtree(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
	}

	// 还原二叉树
	public static TreeNode buildtree(int[] preorder, int pleft, int pright, int[] inorder, int ileft, int iright) {
		if (pleft > pright || ileft > iright) {
			return null;
		}
		// 根节点值是前序遍历的第一个
		TreeNode root = new TreeNode(preorder[pleft]);
		// 中序遍历第一个为起始点
		int middle = ileft;
		// 左子树节点长度
		int len = 0;
		// 找到中序遍历中的根节点位置记为middle
		for (; middle < inorder.length; middle++) {
			if (inorder[middle] == preorder[pleft]) {
				break;
			}
			// 计算左子树节点长度len
			len++;
		}
		// 递归调用求解左右子树
		// 左子树：前序遍历为根后一个到根加左子树长度，中序遍历为第一个到根节点位置前一个
		root.left = buildtree(preorder, pleft + 1, pleft + len, inorder, ileft, middle - 1);
		// 右子树：前序遍历为左子树后一个到最后一个，中序为根节点后一个到最后一个
		root.right = buildtree(preorder, pleft + len + 1, pright, inorder, middle + 1, iright);
		return root;

	}

	public static void cengci(TreeNode root, List<Integer> result) {
		// 确定终止条件
		if (root == null)
			return;

		else {
			// 定义一个队列用于层次遍历二叉树
			Queue<BuildTree1.TreeNode> queue = new LinkedList<>();
			queue.offer(root);// offer方法表示添加元素到队尾
			while (!queue.isEmpty()) {
				BuildTree1.TreeNode temp = queue.poll();// poll方法删除队头元素
				result.add(temp.val);
				if (temp.left != null) {
					queue.offer(temp.left);
				}
				if (temp.right != null) {
					queue.offer(temp.right);
				}
			}
		}
	}

	public static List<Integer> cengciTraversal(TreeNode root) {
		List<Integer> list = new ArrayList<Integer>();
		cengci(root, list);
		return list;
	}

	public static void main(String[] args) {
		System.out.println("输入前序遍历");
		Scanner sc1 = new Scanner(System.in);
		String str1 = sc1.next().toString();
		String[] s1 = str1.split(",");
		int[] qian = new int[s1.length];
		for (int i = 0; i < qian.length; i++) {
			qian[i] = Integer.parseInt(s1[i]);
		}
		System.out.println("输入中序遍历");
		Scanner sc2 = new Scanner(System.in);
		String str2 = sc2.next().toString();
		String[] s2 = str2.split(",");
		int[] zhong = new int[s2.length];
		for (int i = 0; i < zhong.length; i++) {
			zhong[i] = Integer.parseInt(s2[i]);
		}
		sc1.close();
		sc2.close();

		BuildTree1 buildTree1 = new BuildTree1();
		TreeNode r = buildTree1.buildTree(qian, zhong);
		System.out.println(cengciTraversal(r));
	}
}

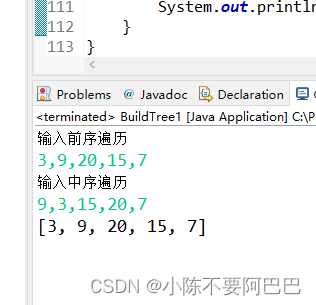
这里答主留下一个疑问，如何将空节点表述出来，可以在评论区讨论一下