机器学习和深度学习已越来越多应用在时序预测中。ARIMA 或指数平滑等经典预测方法正在被 XGBoost、高斯过程或深度学习等机器学习回归算法所取代。
尽管时序模型越来越复杂,但人们对时序模型的性能表示怀疑。
有研究表明,复杂的时序模型并不一定会比时序分解模型有效(Makridakis, 2018)。
技术提升
技术要学会分享、交流,不建议闭门造车。
好的文章离不开粉丝的分享、推荐,资料干货、资料分享、数据、技术交流提升,均可加交流群获取,群友已超过2000人,添加时最好的备注方式为:来源+兴趣方向,方便找到志同道合的朋友。
方式①、添加微信号:dkl88191,备注:来自CSDN
方式②、微信搜索公众号:Python学习与数据挖掘,后台回复:加群
为什么时序预测很难?
时间序列是按时间排序的值,但时序预测具有很大的挑战性。从模型难度和精度角度考虑,时序模型的比常规的回归和分类任务更难。
原因1:序列是非平稳的
平稳性是时间序列的核心概念,如果时间序列的趋势(例如平均水平)不随时间变化,则该时间序列是平稳的。许多现有方法都假设时间序列是平稳的,但是趋势或季节性会打破平稳性。
原因2:依赖外部数据
除了时间因素之外,时间序列通常还有额外的依赖性。时空数据是一个常见的例子,每个观察值都在两个维度上相关,因此数据具有自身的滞后(时间依赖性)和附近位置的滞后(空间依赖性)。
原因3:噪音和缺失值
现实世界受到噪音和缺失值的困扰,设备故障可能会产生噪音和缺失值。传感器故障导致数据丢失,或者存在干扰,都会带来数据噪音。
原因4:样本量有限
时间序列往往都只包含少量的观察值,可能没有足够的数据来构建足够的模型。数据采集的频率影响了样本量,同时也会遇到数据冷启动问题。
样本量与模型精度
时序模型往往无法进行完美预测,这可能和时序数据的样本量相关。在使用较大的训练集时,具有大模型往往比参数较少的模型表现更好。
在时序序列长度小于1000时,深度模型往往并不会比时序分类模型更好。
下面对比了模型精度与样本个数的关系,这里尝试了五种经典方法(ARIMA、ETS、TBATS、Theta 和 Naive)和五种机器学习方法(高斯过程、M5、LASSO、随机森林和 MARS)。预测任务是来预测时间序列的下一个值。
结果如下图所示,轴表示训练样本大小,即用于拟合预测模型的数据量。轴表示所有时间序列中每个模型的平均误差,使用交叉验证计算得出。
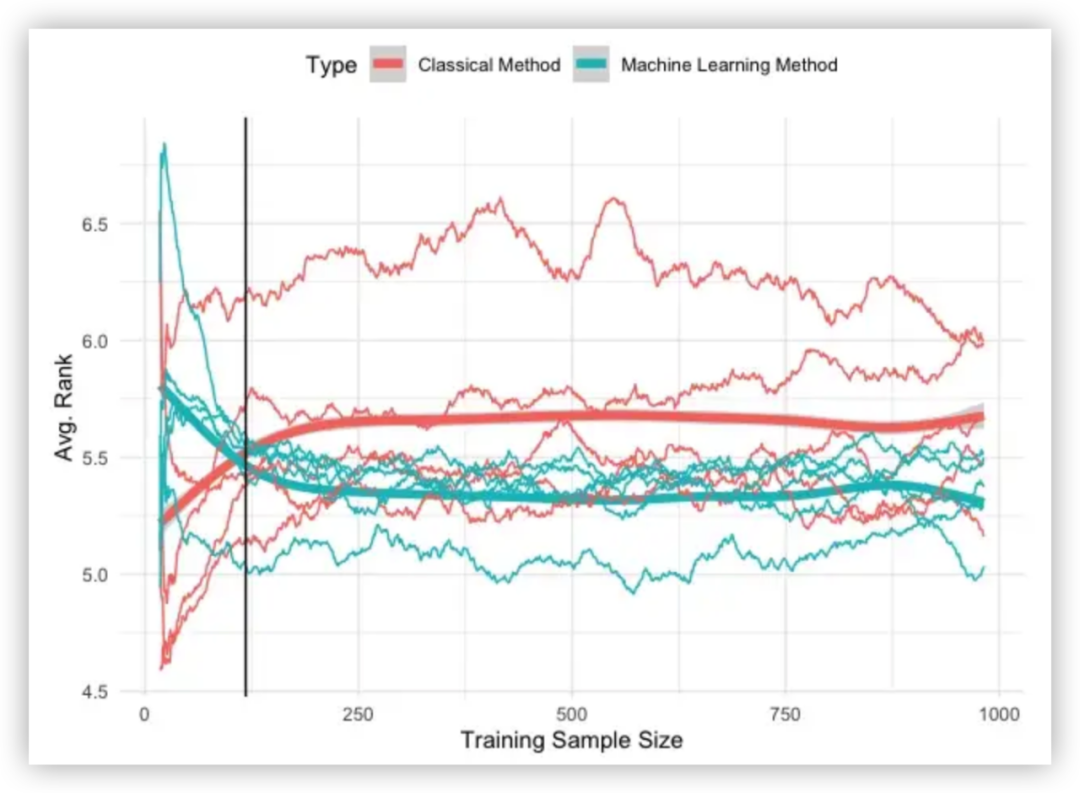
当只有少数观测值可用时,基础方法表现出更好的性能。然而,随着样本量的增加,机器学习方法优于经典方法。
进一步可以得出以下结论:
-
机器学习方法拥有很强的预测能力,前提是它们具有足够大的训练数据集;
-
当只有少量观测值可用时,推荐首选 ARIMA 或指数平滑等经典方法;
-
可以将指数平滑等经典方法与机器学习相结合可以提高预测准确性。
时序多步预测
大多数预测问题都被定义为单步预测,根据最近发生的事件预测系列的下一个值。
时间序列多步预测需要预测未来多个值, 提前预测许多步骤具有重要的实际优势,多步预测减少了长期的不确定性。
但模型试图预测更远的未来时,模型的误差也会逐渐增加。
方法1:递归预测
多步预测最简单的方法是递归形式,训练单个模型进行单步预测,然后将模型与其先前的预测结果作为输入得到后续的输出。
from sklearn.linear_model import LinearRegression
# using a linear regression for simplicity. any regression will do.
recursive = LinearRegression()
# training it to predict the next value of the series (t+1)
recursive.fit(X_tr, Y_tr['t+1'])
# setting up the prediction data structure
predictions = pd.DataFrame(np.zeros(Y_ts.shape), columns=Y_ts.columns)
# making predictions for t+1
yh = recursive.predict(X_ts)
predictions['t+1'] = yh
# iterating the model with its own predictions for multi-step forecasting
X_ts_aux = X_ts.copy()
for i in range(2, Y_tr.shape[1] + 1):
X_ts_aux.iloc[:, :-1] = X_ts_aux.iloc[:, 1:].values
X_ts_aux['t-0'] = yh
yh = recursive.predict(X_ts_aux)
predictions[f't+{i}'] = yh
上述代码逻辑在sktime中也可以找到相应的实现:https://www.sktime.org/en/stable/api_reference/auto_generated/sktime.forecasting.compose.RecursiveTimeSeriesRegressionForecaster.html
递归方法只需要一个模型即可完成整个预测范围,且无需事先确定预测范围。
但此种方法用自己的预测作为输入,这导致误差逐渐累计,对长期预测的预测性能较差。
方法2:多目标回归
多目标回归为每一个预测结果构建一个模型,如下是一个使用案例:
from sklearn.multioutput import MultiOutputRegressor
direct = MultiOutputRegressor(LinearRegression())
direct.fit(X_tr, Y_tr)
direct.predict(X_ts)
scikit-learn的
MultiOutputRegressor
为每个目标变量复制了一个学习算法。在这种情况下,预测方法是
LinearRegression
。
此种方法避免了递归方式中错误传播,但多目标预测需要更多的计算资源。此外多目标预测假设每个点是独立的,这是违背了时序数据的特点。
方法3:递归多目标回归
递归多目标回归结合了多目标和递归的思想。为每个点建立一个模型。但是在每一步的输入数据都会随着前一个模型的预测而增加。
from sklearn.multioutput import RegressorChain
dirrec = RegressorChain(LinearRegression())
dirrec.fit(X_tr, Y_tr)
dirrec.predict(X_ts)
这种方法在机器学习文献中被称为
chaining
。scikit-learn 通过 RegressorChain 类为其提供了一个实现。
参考文献
Makridakis, Spyros, Evangelos Spiliotis, and Vassilios Assimakopoulos. “Statistical and Machine Learning forecasting methods: Concerns and ways forward.” PloS one 13.3 (2018): e0194889.