1.一般的泛函就是把函数作为元素来研究的一门学科,泛函分析,举个简单一点的列子,我们以前学的函数是把数字作为基本的元素来研究的,现在更高一个层次,就是元素就是一个函数,比如全体实系数连续函数构成一个集合A,那么这个A中每一个元素就是一个函数,而泛函就是研究在类似于A这种集合到数之间的关系,比如在定义一个A到实数R的映射f(x),那么x就代表一个函数,所以有些人也称为是研究函数的函数,不过这只是粗略介绍而已,详情你要自己学了就知道
2.泛函也是一种“函数”,它的独立变量一般不是通常函数的“自变量”,而是通常函数本身。泛函是函数的函数。由于函数的值是由自变量的选取而确定的,而泛函的值是由自变量函数确定的,故也可以将其理解为函数的函数。泛函的自变量是函数,泛函的自变量称为宗量。简言之,泛函就是函数的函数。 3.如果连续泛函满足下列条件J( x1(t)+x2(t))=J(x1(t))+J(x2(t)) J(Cx(t))=CJ(x(t))其中C为任意常数,就称之为线形泛函。如果连续泛函满足下列条件:J(x1(t))+J(x2(t))=0.5(J(x1(t)+x2(t))+J(x1(t)-x2(t)))且J(Cx(t))=C^2J(x(t)),就称之为二次性泛函。
LQR (linear quadratic regulator)即
线性
二次型
调节器,其对象是现代控制理论中以
状态空间
形式给出的
线性系统
,而
目标函数
为对象状态和控制输入的二次型函数。
LQR 的直观推导及简单应用
https://blog.csdn.net/heyijia0327/article/details/39270597
LQR控制器是怎么计算反馈矩阵K的: 1.选择参数矩阵Q,R 2.求解Riccati 方程得到矩阵P 3.计算
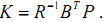
最优控制理论总结——动态规划
https://blog.csdn.net/u014157632/article/details/53313109
最优控制
在满足一定约束的情况下,寻求最优控制策略,使得性能指标取极大值或极小值 对一个受控的动力学系统,从一类允许的控制方案中寻找一个最优的控制方案,使得系统的运动从由某个初始状态转移到目标状态的同时,其性能指标值为最优
性质
在一般的情况下,由极大值原理算出的最优控制是时间t的函数u(t),称为程序控制或者开环控制称为程序控制或者开环控制程序控制的主要缺点,是不能消除或者抑制由于参数的变动和环境的变化对系统造成的扰动,也就是鲁棒性很差 最优控制的另一种形式是表示为状态变量x(t)的函数u(x),实际上一种状态反馈,称为综合控制或者闭环控制,其优点是能有效抑制扰动
解决方法
最优控制本质是变分问题,经典变分理论只能解决一类简单的最优控制问题
现代变分理论最常用的就是极大值原理和动态规划
按照控制作用实现方法分类,有开环最优控制和闭环最优
古典变分法
研究对泛函求极值的一种数学方法,只能用在控制变量的取值范围不受限的情况
极大值原理
(庞特里亚金)是分析力学中哈密尔顿方法的推广,其突出的优点是可以用于控制变量受限的情况
动态规划
(贝尔曼)其为数学规划的一种,同样可用于控制变量受限的情况,是一种适合于在计算机上进行计算的比较有效的方法
最优化方法
(也称做运筹学方法)是近几十年形成的,它主要运用数学方法研究各种系统的优化途径及方案,为决策者提供科学决策的依据。最优化方法的主要研究对象是各种有组织系统的管理问题及其生产经营活动。最优化方法的目的在于针对所研究的系统,求得一个合理运用人力、物力和财力的最佳方案,发挥和提高系统的效能及效益,最终达到系统的最优目标。
主要分支
线性规划
当目标函数f是线性函数而且集合A是由线性等式函数和线性不等式函数来确定的, 我们称这一类问题为线性规划
整数规划
当线性规划问题的部分或所有的变量局限于整数值时, 我们称这一类问题为整数规划问题
二次规划
目标函数是二次函数,而且集合A必须是由线性等式函数和线性不等式函数来确定的。
非线性规划
研究的是目标函数或是限制函数中含有非线性函数的问题。
随机规划
研究的是某些变量是随机变量的问题。
动态规划
研究的是最优策略基于将问题分解成若干个较小的子问题的优化问题。
组合最优化
研究的是可行解是离散或是可转化为离散的问题。
无限维最优化
研究的是可行解的集合是无限维空间的子集的问题,一个无限维空间的例子是函数空间