文章目录
(0)参考链接
(1)OpenCV学习笔记(七) 相机标定的函数理解与学习:
https://blog.csdn.net/xuxunjie147/article/details/79219774
(2)张正友标定算法原理详解(二):
https://blog.csdn.net/weixin_36340947/article/details/78246094
(3)余文勇《机器视觉自动检测技术》 化学工业出版社
(4)Adrian Kaehler 《学习OpenCV3(中文版)》 清华大学出版社
(5)章敏晋 《计算机视觉教程》 人民邮电出版社
(6)Milan Sonka 《图像处理、分析与机器视觉》
(1)标定理论
<0>标定板
原则上,任何实当标志的物体都可以用作标定物。一个实际的选择是平面上的规则图像,如棋盘、圆网格、随机图案、ArUco或ChArUco图案。
在opencv_contrib-3.3.1\modules\ccalib\samples目录下还有random_pattern_generator,可用于多相机标定,而ArUco或ChArUco图案来自增强现实二维码(ArUco),优点在于,不需要在标签上找到标定的角点。
  
**图1-1 各种标定板**
<1>为什么要进行相机标定
计算机视觉的基本任务之一是从摄像机获取的图像信息出发,计算三维空间中的几何信息,并由此重建和识别物体;**而空间物体表面某点的三维几何与其在图像中对应点之间的相互关系是由摄像机成像的几何模型决定的,这些几何模型参数就是摄像机参数。**在大多数条件下,这些参数必须通过实验与计算才能得到,这个过程被称为摄像机标定。
标定过程就是直接确定摄像机的几何和光学参数
,摄像机相当于世界坐标系的方位,标定精度的大小,直接影响着计算机视觉(机器视觉)的精度。
####<2>相机标定的分类
①根据是否需要标定参照物
可分为传统的摄像机标定方法和摄像机自标定方法。**传统的摄像机标定是在一定的摄像机模型下,基于特定的实验条件。如形状、尺寸已知的标定物,经过对其进行图像处理,利用一系列数学变换和计算方法,求取摄像机模型的内部参数和外部参数;**不依赖于标定参照物的摄像机标定方法,
仅利用摄像机在运动过的中周围环境的图像与图像之间的对应关系对摄像机进行的标定称为摄像机自标定方法
,又分为基于自动视觉的摄像机自标定技术(基于平移运动的自标定技术和基于旋转运动的自标定技术)、利用本质矩阵和基本矩阵的自标定技术、利用多幅图像之间的直线对应关系的摄像机自标定方法记忆利用灭点和通过弱透视投影或平行透视投影进行摄像机标定等。自标定方法非常灵活,但未知参数太多,很难得到稳定的结果。
一般来说,当应用场合所要求的精度很高,且摄像机的参数不经常变换时,传统标定方法为首选。而自标定方法主要应用于精度要求不高的场合,例如虚拟现实等。
②根据所用模型
可分为线性和非线性两种。
1)线性模型
所谓的线性模型,是指经典的小孔模型。线性模型摄像机标定,用线性方程求解,简单快速。但其不考虑镜头畸变,准确性欠佳。
2)非线性模型
成像过程不服从小孔模型的称为摄像机的非线性模型。其考虑了畸变参数,引入了非线性优化,但方法较繁,速度慢,对初值选择和噪声比较敏感。
③根据所用摄像机个数不同
在双目立体视觉中,还要确定两个摄像机之间的相对位置和方向。
④根据标定块的不同有立体和平面
定标通过拍摄一个事先已知确定了三维几何形状的物体来进行,也就是在一定的摄像机模型下,基于特定的实验条件人形状、尺寸已知的定标参照物(标定物),经过对其图像进行处理,利用一系列数学变换和计算方法,求取摄像机模型的内部参数和外部参数。这种定标方法的精度很高。用于定标的物体一般是由两到三个相互正交的平面组成。但这些方法需要提取图像上的网格角点,平面模板与图像间的网格角点对应关系,对应了单应性矩阵,平面模板可以用硬纸板,上面张贴激光打印机打印的棋盘格。模板图案常采用矩形和二次曲线(圆和椭圆)。
⑤根据内部参数是否可变的角度
可以分为可变内部参数的定标和不可变内部参数的定标。
⑥从求解参数的结果来看有显示和隐式
隐参数定标是以一个转换矩阵表示空间物点与二维想点的对应关系,并以转换矩阵元素作为定标参数,由于这些参数没有具体的物理意义,所以称为隐参数定标。
在精度要求不高的情况下,只需要求解线性方程,此可以获得较高的效率。DLT定标(直接线性标定)是典型的针孔相机模型。为了提高标定精度,就需要通过精确分析摄像机成像的中间过程,构造精密的几何模型,设置具有物理意义的参数,然后确定这些位置参数,实现摄像机
的显参数标定。
#####⑦解题方法来看
空间点与其图像对应点之间是一种复杂的非线性关系,用图像中的像素位置难以准确计算实际空间点间的实际尺寸。解析方法是用足够多的点的世界坐标和相应的图像坐标,通过解析公式来确定摄像机的内参数、外参数以及畸变参数,再将图像中的点通过几何关系得到空间点的世界坐标。神经网络方法能够以任意精度逼近任何非线性关系,跳过求取各参数的繁琐过程,利用图坐标点和相关的空间点作为输入输出样本集进行训练,使网络实现给定的输入输出映射关系,对于不是样本集合中的图像坐标点也能得到合适的空间点的世界坐标
#####⑧从定标步骤看
分为两步法、三步法、四步法等;
#####⑨从运动方式上看
分为非限定运动方式的摄像机定标和不可变内部参数的定标;
(2)标定过程(以棋盘格为例)
<1>准备好棋盘格图像(借一下师兄的图片)

**图1-1 准备好的棋盘格图像**
<2>寻找棋盘格角点
给定一个棋盘图像(一个人手持期盼,或任何具有棋盘的场景和合适的无干扰背景),可以使用下面函数来定位棋盘的角点。
bool cv::findChessboardCorners(cv::InputArray image,cv::Size pattenSize,cv::OutputArray corners,int flags = cv::CALIB_CB_ADAPTIVE_THRESH|cv::CALIB_CB_NORMALIZE_IMAGE)
这个函数将包含棋盘的单个图像作为输入参数,该图像应该是8比特图像(8UC1 or 8UC3),第二个参数pattenSize表示棋盘的每行和每列有多少角点,这个值是内角点数,因此,对于一个标准的西洋棋棋盘,如图1-2所示,正确的值是cv::Size(7,7)。参数corners是记录角点位置的输出矩阵,用像素坐标来表示角点位置的每个值,最后的参数flags用于实现一个或多个附加滤波步骤,以帮助找到棋盘上的角点。
cv::CALIB_CB_ADAPTIVE_THRESH 根据平均亮度对图像进行阈值化,使用自适应阈值方法
cv::CALIB_CB_NORMALIZE_IMAGE 使用cv::equalizeHist()归一化图像
cv::CALIB_CB_FULTER_QUADS 一旦图像阈值化,就会尝试从棋盘上的黑色方块的透视图中找出四边形,这就是一个近似。因为假设四边形的每个边缘的线是直的,当图像中存在径向畸变时,就会不正确。对四边形应用各种附加约束,以防出现错误的四边形
cv::CALIB_CV_FAST_CHECK 对图像进行快速扫描,确保图像中存在角点,如果不存在,则跳过此图像,在输入中存在没有棋盘的图像,使用该标志会节省大量时间。
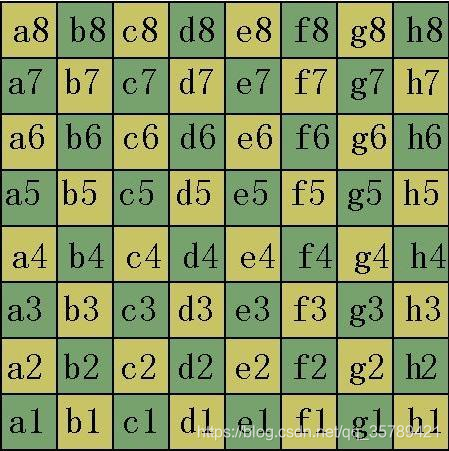
**图1-2 标准的西洋棋棋盘(8*8=64)**
**<3>寻找棋盘格上的亚像素角点** 为了提高标定精度,需要在初步提取的角点信息上进一步提取亚像素信息,降低相机标定偏差,常用的方法是cornerSubPix,cornerSubPix()使用内部算法仅提供角点的近似位置,这些位置是相对准确的。另一个方法是使用find4QuadCornerSubpix函数,这个方法是专门用来获取棋盘图上内角点的精确位置的。 >两函数都出自“Camera Calibration and 3D Reconstruction”,在官方文档的描述中,对于find4QuadCornerSubpix函数的描述为”finds subpixel-accurate positions of the chessboard corners(找到棋盘转角的亚像素精确位置)”;而对于cornerSubPix()函数的描述则是出现在findChessboardCorners()函数,原文为“The detected coordinates are approximate, and to determine their positions more accurately, the function calls cornerSubPix. You also may use the function cornerSubPix with different parameters if returned coordinates are not accurate enough.(检测到的坐标是近似的,为了更准确地确定它们的位置,函数调用cornerSubPix。如果返回的坐标不够精确,还可以使用带有不同参数的函数cornerSubPix)”。 结果输入三通道图片,find4QuadCornerSubpix()函数抛出了异常,如下图所示:
bool find4QuadCornerSubpix(InputArray img, InputOutputArray corners, Size region_size); //该函数只支持单通道图像
第一个参数img,输入的Mat矩阵,最好是8位灰度图像,检测效率更高;
第二个参数corners,初始的角点坐标向量,同时作为亚像素坐标位置的输出,所以需要是浮点型数据,一般用元素是Pointf2f/Point2d的向量来表示:vector<Point2f/Point2d> iamgePointsBuf;
第三个参数region_size,角点搜索窗口的尺寸;1. 根据输入的搜索窗口的尺寸,确定以该角点为中心的ROI区域,并计算该区域的直方图;2. 找出直方图中最大的一段segment_hist_max,据此进行图像二值化,之后进行腐蚀操作,共进行两次;3. 对两幅图使用findContours进行轮廓提取,对于轮廓根据到该角点的最小距离排序;4. 以每幅图最小的两个轮廓为研究对象,先进行多边形逼近approxPolyDP,并使用findCorner找到轮廓中到该角点最近的点;5. 对找到的四个点使用findLinesCrossPoint,获取精确的角点位置。
在棋盘标定图上绘制找到的内角点(非必须,仅为了显示)
void drawChessboardCorners( InputOutputArray image, Size patternSize, InputArray corners, bool patternWasFound );
第一个参数image,8位灰度或者彩色图像;
第二个参数patternSize,每张标定棋盘上内角点的行列数;
第三个参数corners,初始的角点坐标向量,同时作为亚像素坐标位置的输出,所以需要是浮点型数据,一般用元素是Pointf2f/Point2d的向量来表示:vector<Point2f/Point2d> iamgePointsBuf;
第四个参数patternWasFound,标志位,用来指示定义的棋盘内角点是否被完整的探测到,true表示别完整的探测到,函数会用直线依次连接所有的内角点,作为一个整体,false表示有未被探测到的内角点,这时候函数会以(红色)圆圈标记处检测到的内角点;patternWasFound=ture时,依次连接各个内角点,patternWasFound=false时,以(红色)圆圈标记处角点位置。
<4>镜头畸变
光学系统并不是精确地按照理想化的小孔成像原理工作,存在有透镜像差,像差主要考虑:径向畸变、偏心畸变和薄棱镜畸变。第一类只产生径向位置的偏差,后两类既产生径向位置的偏差,又产生切向偏差。
由于装配误差,组成光学系统的多个光学镜头的光轴不可能完全共线,从而引起偏心形变,这种变形是由径向和切向变形分量共同构成的。薄棱镜变形是光学镜头制造误差和成像敏感阵列制作误差引起的图像变形,其影响同装配误差一样。如下图所示:
![\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jLeCBxRg-1622869472903)(./1622194202776.png)\]](https://img-blog.csdnimg.cn/20210605130834792.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzM1Nzg5NDIx,size_16,color_FFFFFF,t_70)
**图1-3 镜头畸变示意图**
实际光学系统所称的像的差异叫像差。其可以写为孔径(h和sinU)和视场(w或y)的函数,及光学系统的结构参数(r,d,n)的函数,为便于分析,常把像差展开成孔径和视场的级数: $$ \Delta A’=\sum_{i=1}^{\infty} T_iU_i^my_i^n $$ 其中,$\Delta A’$代表某一种像差。$U_i^m$是$U$的$m_i$次方,$y_i^n$是$y$的$n_i$次方。 光学镜头径向曲率变化是引起径向变形的主要原因,导致图像点沿径向移动,离中心点越远,切向形变量越大。其表达式如下: $$ \delta X_r=k_1X_d(X_d^2+Y_d^2)+o[(X_d,Y_d)^5] $$ $$ \delta Y_r=k_1Y_d(X_d^2+Y_d^2)+o[(X_d,Y_d)^5] $$
<5>相机标定
①相关函数
获取到棋盘标定图的内角点图像坐标之后,就可以使用calibrateCamera函数进行标定,计算相机内参和外参系数。
double calibrateCamera ( InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints, Size imageSize, CV_OUT InputOutputArray cameraMatrix, CV_OUT InputOutputArray distCoeffs, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, int flags=0, TermCriteria criteria = TermCriteria (TermCriteria::COUNT+TermCriteria::EPS, 30,DBL_EPSILON) );
第一个参数objectPoints,为世界坐标系中的三维点。在使用时,应该输入一个三维坐标点的向量的向量,即vector<vector> object_points。需要依据棋盘上单个黑白矩阵的大小,计算出(初始化)每一个内角点的世界坐标。
第二个参数imagePoints,为每一个内角点对应的图像坐标点。和objectPoints一样,应该输入vector<vector> image_points_seq形式的变量;
第三个参数imageSize,为图像的像素尺寸大小,在计算相机的内参和畸变矩阵时需要使用到该参数;
第四个参数cameraMatrix为相机的内参矩阵。输入一个Mat cameraMatrix即可,如Mat cameraMatrix=Mat(3,3,CV_32FC1,Scalar::all(0));
第五个参数distCoeffs为畸变矩阵。输入一个Mat distCoeffs=Mat(1,5,CV_32FC1,Scalar::all(0))即可;
第六个参数rvecs为旋转向量;应该输入一个Mat类型的vector,即vectorrvecs;
第七个参数tvecs为位移向量,和rvecs一样,应该为vector tvecs;
第八个参数flags为标定时所采用的算法。有如下几个参数:
CV_CALIB_USE_INTRINSIC_GUESS:使用该参数时,在cameraMatrix矩阵中应该有fx,fy,u0,v0的估计值。否则的话,将初始化(u0,v0)图像的中心点,使用最小二乘估算出fx,fy。
CV_CALIB_FIX_PRINCIPAL_POINT:在进行优化时会固定光轴点。当CV_CALIB_USE_INTRINSIC_GUESS参数被设置,光轴点将保持在中心或者某个输入的值。
CV_CALIB_FIX_ASPECT_RATIO:固定fx/fy的比值,只将fy作为可变量,进行优化计算。当CV_CALIB_USE_INTRINSIC_GUESS没有被设置,fx和fy将会被忽略。只有fx/fy的比值在计算中会被用到。
CV_CALIB_ZERO_TANGENT_DIST:设定切向畸变参数(p1,p2)为零。
CV_CALIB_FIX_K1,…,CV_CALIB_FIX_K6:对应的径向畸变在优化中保持不变。
CV_CALIB_RATIONAL_MODEL:计算k4,k5,k6三个畸变参数。如果没有设置,则只计算其它5个畸变参数。
第九个参数criteria是最优迭代终止条件设定。在使用该函数进行标定运算之前,需要对棋盘上每一个内角点的空间坐标系的位置坐标进行初始化,标定的结果是生成相机的内参矩阵cameraMatrix、相机的5个畸变系数distCoeffs,另外每张图像都会生成属于自己的平移向量和旋转向量。
②标定参数
采用两级标定法对摄像机进行标定(先外部参数,后内部参数)。先计算一组参数
s
i
(
i
=
1
,
2
,
3
,
4
)
s_i(i=1,2,3,4)
s
i
(
i
=
1
,
2
,
3
,
4
)
,已知世界坐标系
(
X
i
,
Y
i
,
Z
i
)
(X_i,Y_i,Z_i)
(
X
i
,
Y
i
,
Z
i
)
和它们对应的图像平面坐标
(
x
i
,
y
i
)
(x_i,y_i)
(
x
i
,
y
i
)
的点,构造一个矩阵A,其中的行
a
i
a_i
a
i
可表示如下:
a
i
=
[
y
i
X
i
y
i
Y
i
−
x
i
X
i
−
x
i
Y
i
y
i
]
a_i=\begin{bmatrix}y_iX_i&y_iY_i&-x_iX_i&-x_iY_i&y_i\end{bmatrix}
a
i
=
[
y
i
X
i
y
i
Y
i
−
x
i
X
i
−
x
i
Y
i
y
i
]
再设
s
i
s_i
s
i
与旋转参数
r
1
,
r
2
,
r
4
,
r
5
r_1,r_2,r_4,r_5
r
1
,
r
2
,
r
4
,
r
5
和平移参数
T
x
,
T
y
T_x,T_y
T
x
,
T
y
有如下的联系:
s
1
=
r
1
/
T
y
,
s
2
=
r
2
/
T
y
,
s
3
=
r
4
/
T
y
,
s
4
=
r
5
/
T
y
,
s
5
=
T
x
/
T
y
s_1=r_1/T_y,s_2=r_2/T_y,s_3=r_4/T_y,s_4=r_5/T_y,s_5=T_x/T_y
s
1
=
r
1
/
T
y
,
s
2
=
r
2
/
T
y
,
s
3
=
r
4
/
T
y
,
s
4
=
r
5
/
T
y
,
s
5
=
T
x
/
T
y
设
u
=
[
x
1
x
2
⋯
x
M
]
T
u=\begin{bmatrix} x_1 & x_2 &\cdots & x_M\end{bmatrix}^T
u
=
[
x
1
x
2
⋯
x
M
]
T
,则由线性方程组
A
s
=
u
As=u
A
s
=
u
,可解出s。然后计算各个旋转和平移参数:
设
S
=
s
1
2
+
s
2
2
+
s
3
2
+
s
4
S=s_1^2+s_2^2+s_3^2+s^4
S
=
s
1
2
+
s
2
2
+
s
3
2
+
s
4
,计算
T
y
2
{
S
−
[
S
2
−
4
(
s
1
s
4
−
s
2
s
3
)
2
]
1
2
2
(
s
1
s
4
−
s
2
s
3
)
2
s
1
s
4
−
s
2
s
3
≠
0
1
s
1
2
+
s
2
2
s
1
2
+
s
2
2
≠
0
1
s
3
2
+
s
4
2
s
3
2
+
s
4
2
≠
0
T_y^2\begin{cases} \frac{S-[S^2-4(s_1s_4-s_2s_3)^2]^\frac{1}{2}}{2(s_1s_4-s_2s_3)^2} & s_1s_4-s_2s_3 \neq 0\\\frac{1}{s_1^2+s_2^2} & s_1^2+s_2^2\neq 0 \\ \frac{1}{s_3^2+s_4^2} & s_3^2+s_4^2\neq 0\end{cases}
T
y
2
⎩
⎪
⎪
⎨
⎪
⎪
⎧
2
(
s
1
s
4
−
s
2
s
3
)
2
S
−
[
S
2
−
4
(
s
1
s
4
−
s
2
s
3
)
2
]
2
1
s
1
2
+
s
2
2
1
s
3
2
+
s
4
2
1
s
1
s
4
−
s
2
s
3
=
0
s
1
2
+
s
2
2
=
0
s
3
2
+
s
4
2
=
0
设
T
y
=
(
T
y
2
)
1
2
T_y=(T_y^2)^\frac{1}{2}
T
y
=
(
T
y
2
)
2
1
,即取正的平方根,计算
r
1
=
s
1
T
y
,
r
2
=
s
2
T
y
,
r
4
=
s
3
T
y
,
r
5
=
s
4
T
y
,
T
x
=
s
5
T
y
r_1=s_1T_y,r_2=s_2T_y,r_4=s_3T_y,r_5=s_4T_y,T_x=s_5T_y
r
1
=
s
1
T
y
,
r
2
=
s
2
T
y
,
r
4
=
s
3
T
y
,
r
5
=
s
4
T
y
,
T
x
=
s
5
T
y
,选一个世界坐标系为(X.Y,Z)的点,要求其图像平面坐标(x,y)离图像中心点较远,计算
p
x
=
r
1
X
+
r
2
Y
+
T
x
,
p
y
=
r
4
X
+
r
5
Y
+
T
y
p_x=r_1X+r_2Y+T_x,p_y=r_4X+r_5Y+T_y
p
x
=
r
1
X
+
r
2
Y
+
T
x
,
p
y
=
r
4
X
+
r
5
Y
+
T
y
,相当于算出旋转参数应用与点(X,Y,Z)的X和Y、如果
p
x
p_x
p
x
和的符号一致,则说明
T
y
T_y
T
y
已有正确符号,否则对
T
y
T_y
T
y
取负。计算其他旋转参数:
r
3
=
(
1
−
r
1
2
−
r
2
2
)
1
2
,
r
6
=
(
1
−
r
4
2
−
r
5
2
)
1
2
,
r
7
=
1
−
r
1
2
−
r
2
r
4
r
3
,
r
8
=
1
−
r
2
r
4
−
r
5
2
r
6
,
r
9
=
(
1
−
r
3
r
7
−
r
6
r
8
)
1
2
r_3=(1-r_1^2-r_2^2)^\frac{1}{2},r_6=(1-r_4^2-r_5^2)^\frac{1}{2},r_7=\frac{1-r_1^2-r_2r_4}{r_3},r_8=\frac{1-r_2r_4-r_5^2}{r_6},r_9=(1-r_3r_7-r_6r_8)^\frac{1}{2}
r
3
=
(
1
−
r
1
2
−
r
2
2
)
2
1
,
r
6
=
(
1
−
r
4
2
−
r
5
2
)
2
1
,
r
7
=
r
3
1
−
r
1
2
−
r
2
r
4
,
r
8
=
r
6
1
−
r
2
r
4
−
r
5
2
,
r
9
=
(
1
−
r
3
r
7
−
r
6
r
8
)
2
1
如果
r
1
r
4
+
r
2
r
5
r_1r_4+r_2r_5
r
1
r
4
+
r
2
r
5
的符号为正,则
r
6
r_6
r
6
要取负,而
r
7
r_7
r
7
和
r
8
r_8
r
8
的符号要在计算完焦距
λ
\lambda
λ
后调整,建立另一组线性方程来计算焦距
λ
\lambda
λ
和z方向的平移参数
T
z
T_z
T
z
,可先构建一个矩阵B,其中行
b
i
b_i
b
i
可表示为
b
1
=
[
r
4
X
i
+
r
5
Y
i
+
T
y
y
i
]
b_1=\begin{bmatrix} r_4X_i+r_5Y_i+T_y & y_i\end{bmatrix}
b
1
=
[
r
4
X
i
+
r
5
Y
i
+
T
y
y
i
]
,设矢量v的行
v
i
v_i
v
i
可表示为:
v
i
=
(
r
7
X
i
+
r
8
Y
i
)
y
i
v_i=(r_7X_i+r_8Y_i)y_i
v
i
=
(
r
7
X
i
+
r
8
Y
i
)
y
i
,由线性方程组
B
t
=
v
Bt=v
B
t
=
v
可解出
t
=
[
λ
T
z
]
T
t=\begin{bmatrix}\lambda &T_z \end{bmatrix}^T
t
=
[
λ
T
z
]
T
,这里得到的只是对t的估计,如果
λ
<
0
\lambda <0
λ
<
0
,则使用右手坐标系统;利用对t的估计来计算镜头的径向失真k,并改进对
λ
\lambda
λ
和
T
z
T_z
T
z
的取值。可得到下面非线性方程:
y
i
(
1
+
k
r
2
)
=
λ
r
4
X
i
+
r
5
Y
i
+
r
6
Z
i
+
T
y
r
7
X
i
+
r
8
Y
i
+
r
9
Z
i
+
T
z
i
=
1
,
2
,
⋯
,
M
\begin{matrix}{y_i(1+kr^2)=\lambda \frac{r_4X_i+r_5Y_i+r_6Z_i+T_y}{r_7X_i+r_8Y_i+r_9Z_i+T_z}} &i=1,2,\cdots,M\end{matrix}
y
i
(
1
+
k
r
2
)
=
λ
r
7
X
i
+
r
8
Y
i
+
r
9
Z
i
+
T
z
r
4
X
i
+
r
5
Y
i
+
r
6
Z
i
+
T
y
i
=
1
,
2
,
⋯
,
M
用非线性回归方法解出上述方程即可得到k,
λ
\lambda
λ
和
T
z
T_z
T
z
的值。
③标定过程
第一步,需标定的参数是旋转矩阵R和平移矩阵T,第二步,需标定的参数是焦距
λ
\lambda
λ
,第三步,需标定的参数是镜头径向失真系数
k
k
k
,第四步,需标定的参数是不确定性图像尺度因子
μ
\mu
μ
。
外部参数标定程序的第一步是从3-D世界坐标系统变换到其中心在摄像机光学中心的3-D坐标系统,其变换参数称为外部参数,即摄像机姿态参数。旋转矩阵
R
R
R
一共有9个元素,单实际上只有三个自由度,可借助刚体转动的3个欧拉角来表示。
内部参数后三步是从摄像机坐标系统中的3-D坐标变换到计算机图像坐标系统中的2-D坐标,其变换参数称为内部参数。一共有五个:焦距
λ
\lambda
λ
、镜头失真系数
k
k
k
、不确定性图像尺度因子
μ
\mu
μ
、图像平面原点
O
m
O_m
O
m
、计算机图像坐标原点
O
n
O_n
O
n
。
将一个完整的摄像机标定变换矩阵
C
C
C
分解为内部参数矩阵
C
i
C_i
C
i
和外部参数矩阵
C
e
C_e
C
e
的乘积:
C
=
C
i
C
e
C=C_iC_e
C
=
C
i
C
e
C
i
C_i
C
i
在通常情况下是一个4 x 4的矩阵,但一般可简化成一个3 x 3的矩阵:
C
i
=
[
s
x
p
x
t
x
p
y
s
y
t
y
0
0
1
λ
]
C_i=\begin{bmatrix} s_x & p_x & t_x\\ p_y & s_y & t_y\\ 0 & 0 & \frac{1}{\lambda} \end{bmatrix}
C
i
=
⎣
⎡
s
x
p
y
0
p
x
s
y
0
t
x
t
y
λ
1
⎦
⎤
其中
s
x
s_x
s
x
和
s
y
s_y
s
y
分别是沿X和Y的缩放系数,
p
x
p_x
p
x
和
p
y
p_y
p
y
分别是沿X和Y轴的偏斜系数,
t
x
t_x
t
x
和
t
y
t_y
t
y
分别是沿X和Y轴的平移系数,
λ
\lambda
λ
是镜头的焦距。
C
e
C_e
C
e
的通用形式也是一个4 x 4的矩阵,可写成:
C
e
=
[
R
1
R
1
.
T
R
2
R
2
.
T
R
2
R
2
.
T
0
1
]
C_e=\begin{bmatrix} R_1&R_1 . T\\ R_2&R_2 . T\\ R_2&R_2 . T\\ 0&1 \end{bmatrix}
C
e
=
⎣
⎢
⎢
⎡
R
1
R
2
R
2
0
R
1
.
T
R
2
.
T
R
2
.
T
1
⎦
⎥
⎥
⎤
<6>通过单应性评价标定结果
①单应性
3D计算机视觉的一个常见任务是从点对应计算单应性。对应的意思是有序的点对集合
(
u
i
,
u
i
′
)
i
=
1
m
(u_i,u_i’)_{i=1}^m
(
u
i
,
u
i
′
)
i
=
1
m
,每一个点对在变换中是对应的,这些对应可通过手动输入或者某个算法算法计算得到。
单应性,也认为是共线或投影变换,是
P
d
→
P
d
P^d \to P^d
P
d
→
P
d
的映射,在嵌入空间
R
d
+
1
R^{d+1}
R
d
+
1
是线性的,单应性在相差一个尺度意义下给定,写为
u
′
≃
H
u
u’ \simeq Hu
u
′
≃
H
u
,其中H是$(d+1) \times (d+1)
KaTeX parse error: Expected ‘EOF’, got ‘&’ at position 54: …么不同的点映射到不同的点上。 &̲emsp; Open…
q=sHQ=sMWQ$,其中点q是点Q映射到成像装置上的点。引入任意的比例因子s,通过是从H中分解出来的。M表示相机矩阵,w是一个4×3的旋转矩阵R和平移矩阵T。
KaTeX parse error: Expected ‘EOF’, got ‘&’ at position 49: …\1\end{bmatrix}&̲ensp; p=\b…
可以在不知道相机内参的情况下计算H,多个视图中计算多个单应性矩阵是OpenCV用于求解内存参数的方法。
cv::Mat cv::findHomography(CV::InputArray srcPoints,CV::InputArray dstPoints,cv::int method=0,double ransacReprojThreshold=3,cv::OutputArray mask =cv:::noArray())
srcPoints表示包含原始平面中的点,dstPoints表示目标平面中的点,输入变量method用于计算单应性矩阵所使用的算法,当其为0时,计算使重新投影误差最小,即H乘以”原始”点与目标点之间的欧式距离的平方之和。对于cv::RANSAC(一致性随机抽样),非常有校地避免异常数据地干扰,并找到正确结果;LMeDS背后思想是最小化中位数误差,但必须大部分数据点均为内部点时,效果才好。
(3)标定代码
#include <opencv2\opencv.hpp>
#include <iostream>
void help(char **argv)
{
}
int main(int argc, char **argv)
{
int n_board = 0;
float image_sf = 0.5f;
float delay = 1.f;
int board_w = 0;
int board_h = 0;
if (argc < 4 || argc>0)
{
std::cout << "\n ERROR:Wrong number of input parameters";
help(argv);
return -1;
}
board_w = atoi(argv[1]);
board_h = atoi(argv[2]);
n_board = atoi(argv[3]);
if (argc > 4) delay = atof(argv[4]);
if (argc > 5) image_sf = atof(argv[5]);
int board_n = board_w * board_h;
cv::Size board_sz = cv::Size(board_w, board_h);
cv::VideoCapture capture(0);
if (!capture.isOpened())
{
std::cout << "\nCouldn't Open the camera\n";
help(argv);
return -1;
}
std::vector<std::vector<cv::Point2f>> image_points;
std::vector<std::vector<cv::Point3f>> object_points;
double last_captured_timestamp = 0;
cv::Size image_size;
while (image_points.size() < (size_t)n_board)
{
cv::Mat image0, image;
capture >> image0;
image_size = image0.size();
cv::resize(image0, image, cv::Size(), image_sf, image_sf, cv::INTER_LINEAR);
std::vector<cv::Point2f> corners;
bool found = cv::findChessboardCorners(image, board_sz, corners);
cv::drawChessboardCorners(image, board_sz, corners, found);
double timestamp = static_cast<double>(clock()) / CLOCKS_PER_SEC;
if (found && timestamp - last_captured_timestamp > 1)
{
last_captured_timestamp = timestamp;
image ^= cv::Scalar::all(255);
cv::Mat mcorners(corners);
mcorners *= (1. / image_sf);
image_points.push_back(corners);
object_points.push_back(std::vector<cv::Point3f>());
std::vector<cv::Point3f> &opts = object_points.back();
opts.resize(board_n);
for (int j = 0; j < board_n; j++)
{
opts[j] = cv::Point3f(static_cast<float>(j / board_w), static_cast<float>(j % board_w), 0.f);
}
std::cout << "Collected our" << static_cast<int>(image_points.size()) << "of"<< n_board<<"needed chessboard images\n"<<std::endl;
}
cv::imshow("Calibration", image);
if (cv::waitKey(30) & 255 == 27)
{
return -1;
}
cv::destroyWindow("Calibration");
std::cout << "\n\n*** CALIBRATING THE CAMERA...\n" << std::endl;
cv::Mat intrinsic_matrix, distortion_coeffs;
double err = cv::calibrateCamera(object_points, image_points, image_size, intrinsic_matrix, distortion_coeffs, cv::noArray(), cv::noArray(), cv::CALIB_ZERO_TANGENT_DIST | cv::CALIB_FIX_PRINCIPAL_POINT);
std::cout << "***DONE!\n\nReprojecttion error is" << err << "\nStoring Intrinsics.xml and Distortions.xml files\n\n";
cv::FileStorage fs("intrinsics.xml", cv::FileStorage::WRITE);
fs << "image_width" << image_size.width << "image_height" << image_size.height << "camera_mattix" << intrinsic_matrix << "distortion_coeffcients" << distortion_coeffs;
fs.release();
fs.open("intrinsics.xml", cv::FileStorage::READ);
std::cout << "\nimage width:" << static_cast<int>(fs["image_width"]);
std::cout << "\nimage height:" << static_cast<int>(fs["image_height"]);
cv::Mat intrinsic_matrix_loaded, distortion_coeffs_loaded;
fs["camera_matrix"] >> intrinsic_matrix_loaded;
fs["distortion_cofficients"] >> distortion_coeffs_loaded;
std::cout << "\nintrinsic matrix" << intrinsic_matrix_loaded;
std::cout << "distortion coeffs" << distortion_coeffs_loaded << std::endl;
cv::Mat map1, map2;
cv::initUndistortRectifyMap(intrinsic_matrix_loaded, intrinsic_matrix_loaded, cv::Mat(), intrinsic_matrix_loaded, image_size, CV_16SC2, map1, map2);
for ( ; ; )
{
cv::Mat image, image0;
capture >> image0;
if (image0.empty()) break;
cv::remap(image0, image, map1, map2, cv::INTER_LINEAR, cv::BORDER_CONSTANT, cv::Scalar());
}
cv::imshow("Undistorted", image);
if (cv::waitKey(30) & 255 == 27) break;
}
return 0;
}