博客

目录

前言

一、神经网络概述

二、激活函数

1. 激活函数概述

2. 激活函数的实现

（1）阶跃函数：

（2）sigmoid函数

（3）ReLU函数

总结

前言

神经网络的特性是可以自动地从数据中学习到合适的权重。本节重点关注神经网络进行识别时的处理。本节介绍激活函数。

一、神经网络概述

1. 神经网络分为输入层、中间层（隐藏层）、输出层

2. 下图中的网络一共有三层神经元结构，实质上只有2层神经元有权重，因此将其称为“2层网络”。

二、激活函数

1. 激活函数概述

（1）激活函数会将输入信号的总和转换为输出信号，其作用在于决定如何来激活输入信号的总和。

（2）先计算输入信号加权总和，然后用激活函数转换这一总和

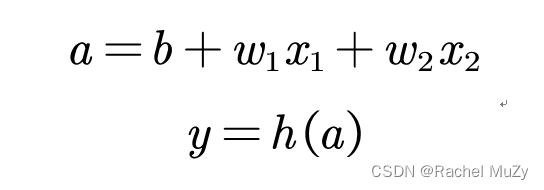
（3）感知机使用阶跃函数作为激活函数，当把激活函数从阶跃函数换成其他函数，就可以进入神经网络的世界。

2. 激活函数的实现

（1）阶跃函数：

可用如下代码实现：

def step_function(x):
    if x > 0:
        return 1
    else:
        return 0

但是参数x只能接受实数（浮点数），但不允许参数取Numpy数组，例如step_function (np.array([1.0, 2.0])，现将其改为支持Numpy数组实现：

import numpy as np

def step_function(x):
    y = x > 0
    return y.astype(np.int)

output = step_function(np.array([-0.0, 1.0, 2.0]))
print(output)

结果：

[0 1 1]

阶跃函数的图形：

import numpy as np
import matplotlib.pylab as plt

def step_function(x):
    return np.array(x > 0, dtype = np.int)

x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) #指定y轴的范围
plt.show

结果：

（2）sigmoid函数

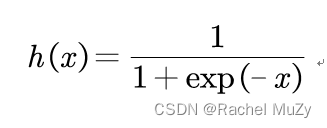
代码：

import numpy as np
import matplotlib.pylab as plt

def sigmoid(x):
    y = 1 / (1 + np.exp(-x))
    return y

inp = np.array([-1.0, 2.0, 1.0, 3.0])
output = sigmoid(inp)
print(output)

结果：

[0.26894142 0.88079708 0.73105858 0.95257413]

画图：

import numpy as np
import matplotlib.pylab as plt

def sigmoid(x):
    y = 1 / (1 + np.exp(-x))
    return y

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) #指定y轴的范围
plt.show

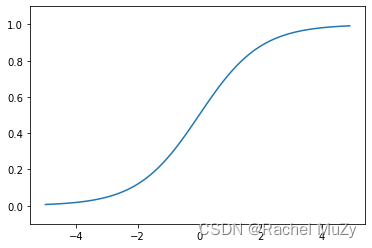
激活函数（1）（2）不同点：

感知机中神经元流动的是0或1的二元信号，神经网络中流动的是连续的实数信号。

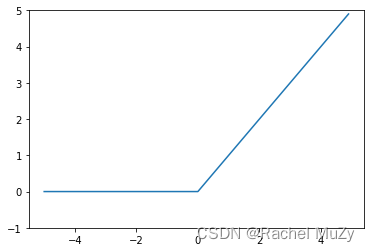
（3）ReLU函数

代码：

import numpy as np
import matplotlib.pylab as plt

def ReLU(x):
    y = np.maximum(0, x)
    return y

x = np.arange(-5.0, 5.0, 0.1)
y = ReLU(x)
plt.plot(x, y)
plt.ylim(-1, 5) #指定y轴的范围
plt.show

结果：

总结

神经网络中的激活函数使用平滑变换的sigmoid函数和ReLU函数。由于今天较忙，下一节将进行多个神经元的搭建。