博客

《剑指Offer》Java刷题 NO.12 数值的整数次方(复现Java pow()函数)

传送门：《剑指Offer刷题总目录》

时间：2020-02-12


题目：


给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。保证base和exponent不同时为0

思路：


（直接连乘效率不高，直接用Math.pow()又有点low，而且效率不如第二种的快速幂算法）


1.降幂递归


注意表示方法：

exp/2可以用exp>>2表示；

(exp%2)= =0可以用exp&1==0表示，位运算效率高




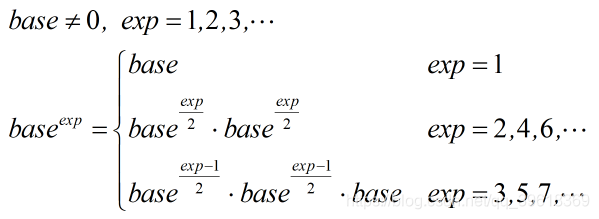
2.快速幂算法：


1.利用指数的二进制分开乘，降低指数大小，

eg：13=1101=1000+0100+0001 
→a^13=a^1101=a^1000*a^0100*a^0001=a^8*a^4*a^1

2.利用&1和<<1逐位读取n，结果为1时就将当前该位代表的乘数乘入结果


注意：

1.指数为负数时，base不能等于0；指数为0时结果为1(0的0次幂无意义)
2.double类型的base不能用base==0.0来判断是否等于0，应该用abs(base)<0.000001来判断

Java代码：

/**
 * 给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。
 * 保证base和exponent不同时为0
 */
public class PowerOfMine {
    /**
     *1.降幂递归
     * 复杂度：O(logN)，但是递归存在时间和内存上的浪费
     */
    public static double pow_1(double base,int exponent){
        if(exponent==0) return 1;
        else if(exponent==1) return base;
        else if(exponent<0){
            if(Math.abs(base)<0.000001)
                throw new RuntimeException("分母不能为0");
            base=1/base;
            exponent=-exponent;
        }
        //exponent是偶数
        if((exponent&1)==0)
            return pow_1(base,exponent>>1)*pow_1(base,exponent>>1);
        exponent是奇数
        else return pow_1(base,(exponent-1)>>1)*pow_1(base,(exponent-1)>>1)*base;
    }
    /**
     * 2.快速幂算法
     * 复杂度：O(logN)
     */
    public static double pow_2(double base,int exponent){
        boolean flag=true;
        if(exponent==0) return 1;
        if (exponent<0){
            if(Math.abs(base)<0.000001)
                throw new RuntimeException("分母不能为0");
            flag=false;
            exponent=-exponent;
        }
        double result=1.0;//最终结果
        double multiplier=base;//乘数项
        while(exponent!=0){
            if((exponent&1)==1)
                result*=multiplier;//该位为1时才把对应位的乘数项乘上去
            multiplier*=multiplier;//每移动一位都将乘数项翻倍
            exponent=exponent>>1;//右移一位，此处exponent>0，所以不用考虑符号的问题
        }
        return flag?result:1/result;
    }

    public static void main(String[] args) {
        System.out.println(pow_2(2.0,-2));
        //System.out.println(pow_2(0,-2));
        System.out.println(pow_2(0,3));
        System.out.println(pow_2(3,0));
        System.out.println(pow_2(-2,3));
        System.out.println(pow_2(-3,-5));
    }
}