背景
- 信用卡欺诈数据,这是个提取好特征的数据
- 用逻辑回归来进行建模
- 数据全部都是数值型的数据,28万左右样本,28个可用的特征,特征整体看上去都在一个量纲内
- Amount特征浮动比较大,需要预处理进行规范化
- 对class进行分类,0:1=284315:492,分布极度不均衡,需要进行处理
对于这种去发现欺诈数据,医疗数据中去发现得病的类别,这类数据的负样本通常比较少,都存在样本分布极度不均衡的情况。
样本不均衡解决办法
下采样:使得两个样本一样少
让多的样本减少到和少的样本一样多的情况。(但是这么做极大的缩小了样本数量;会使得大量原本是正例的样本会被预测成为负例,虽然召回率增加了)
贴代码主要是为了我以后好找,函数太多我记不住。
大概的思路就是把多的样本的index拿出来,然后通过随机函数在里面取得与少的样本一样的数量,然后合并。我自己写代码写的太罗嗦,起名也随意。
X = data.iloc[:, data.columns != 'Class']
y = data.iloc[:, data.columns == 'Class']
# Number of data points in the minority class
number_records_fraud = len(data[data.Class == 1])
fraud_indices = np.array(data[data.Class == 1].index)
# Picking the indices of the normal classes
normal_indices = data[data.Class == 0].index
# Out of the indices we picked, randomly select "x" number (number_records_fraud)
random_normal_indices = np.random.choice(normal_indices, number_records_fraud, replace = False)
random_normal_indices = np.array(random_normal_indices)
# Appending the 2 indices
under_sample_indices = np.concatenate([fraud_indices,random_normal_indices])
# Under sample dataset
under_sample_data = data.iloc[under_sample_indices,:]
X_undersample = under_sample_data.ix[:, under_sample_data.columns != 'Class']
y_undersample = under_sample_data.ix[:, under_sample_data.columns == 'Class']
过采样:生成少的数据,使得一样多
数据造假,这样可能会影响最后的准确率吧
它以每个样本点的k个最近邻样本点为依据,随机的选择N个邻近点进行差值乘上一个[0,1]范围的阈值,从而达到合成数据的目的。这种算法的核心是:
特征空间
上邻近的点其特征都是相似的。它并不是在数据空间上进行采样,而是在特征空间中进行采样,所以它的准确率会高于传统的采样方式。这也是为什么到目前为止SMOTE以及其派生的算法仍然是较为主流的采样技术的原因。
SMOTE上采样
smote算法参考:
探索SMOTE算法 – 知乎
from imblearn.over_sampling import SMOTE
oversampler = SMOTE(random_state=0)
os_features, os_labels = oversampler.fit_resample(features_train, labels_train)
os_features = pd.DataFrame(os_features)
os_labels = pd.DataFrame(os_labels)
数据预处理:数据规范化
from sklearn.preprocessing import StandardScaler
# 1.字段标准化 Z-score x减去均值除以标准差
da_mean = data['Amount'].mean()
da_std = data['Amount'].std()
data['normAmount1'] = ((data['Amount'] - da_mean) / da_std)
da = data['Amount'].values.reshape(-1, 1)
data['normAmount'] = StandardScaler().fit_transform(da)
交叉验证
K折交叉验证获取逻辑回归最优参数C
这里版本不同KFold函数用法不同,可参考
cross_validation.KFold与model_selection.KFold的区别_J符离的博客-CSDN博客
版本不通逻辑回归参数不同,可参考
https://blog.csdn.net/qq_22592457/article/details/103504796
逻辑回归的正则惩罚项参数
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import KFold, cross_val_score
from sklearn.metrics import confusion_matrix,recall_score,classification_report
def printing_Kfold_scores(x_train_data, y_train_data):
fold = KFold(5, shuffle=False)
fold.get_n_splits(x_train_data)
# Different C parameters
c_param_range = [0.01, 0.1, 1, 10, 100]
results_table = pd.DataFrame(index=range(len(c_param_range), 2), columns=['C_parameter', 'Mean recall score'])
results_table['C_parameter'] = c_param_range
# the k-fold will give 2 lists: train_indices = indices[0], test_indices = indices[1]
j = 0
for c_param in c_param_range:
print('-------------------------------------------')
print('C parameter: ', c_param)
print('-------------------------------------------')
print('')
recall_accs = []
for iteration, indices in fold.split(x_train_data):
# Call the logistic regression model with a certain C parameter
lr = LogisticRegression(C=c_param, penalty='l1', solver='liblinear')
lr.fit(x_train_data.iloc[iteration, :], y_train_data.iloc[iteration, :].values.ravel())
y_pred_undersample = lr.predict(x_train_data.iloc[indices, :].values)
# Calculate the recall score and append it to a list for recall scores representing the current c_parameter
recall_acc = recall_score(y_train_data.iloc[indices, :].values, y_pred_undersample)
recall_accs.append(recall_acc)
print('recall score = ', recall_acc)
# The mean value of those recall scores is the metric we want to save and get hold of.
results_table.loc[j, 'Mean recall score'] = np.mean(recall_accs)
j += 1
print('')
print('Mean recall score ', np.mean(recall_accs))
print('')
best_c = results_table.loc[results_table['Mean recall score'].astype(float).idxmax()]['C_parameter']
# Finally, we can check which C parameter is the best amongst the chosen.
print('*********************************************************************************')
print('Best model to choose from cross validation is with C parameter = ', best_c)
print('*********************************************************************************')
return best_c
模型评估标准

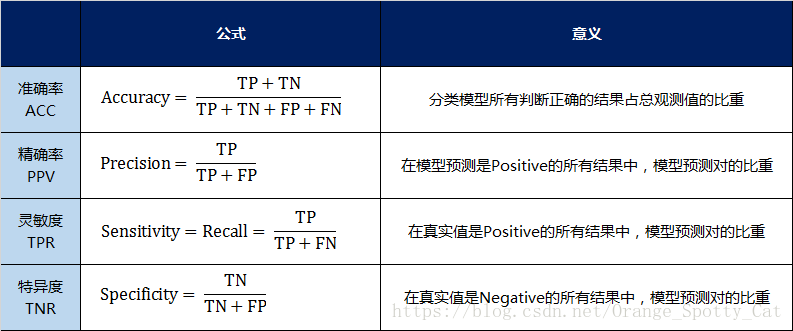
混淆矩阵模板代码
def plot_confusion_matrix(cm, classes,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
"""
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=0)
plt.yticks(tick_marks, classes)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
完整代码
from sklearn.preprocessing import StandardScaler
import seaborn as sns
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split, KFold
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix, classification_report, accuracy_score, recall_score
import itertools
data = pd.read_csv('creditcard.csv')
# 查看类别的比例
'''
0 284315
1 492
'''
data['Class'].value_counts()
# 频率直方图显示类型
count_classes = pd.value_counts(data['Class'], sort=True).sort_index()
count_classes.plot(kind='bar')
plt.title("Fraud class histogram")
plt.xlabel("Class")
plt.ylabel("Frequency")
# 数据处理
# 1.字段标准化 Z-score x减去均值除以标准差
da_mean = data['Amount'].mean()
da_std = data['Amount'].std()
data['normAmount1'] = ((data['Amount'] - da_mean) / da_std)
da = data['Amount'].values.reshape(-1, 1)
data['normAmount'] = StandardScaler().fit_transform(da)
# 删除多余的字段
data = data.drop(['Time', 'Amount'], axis=1)
# 查看相关性
figure, ax = plt.subplots(figsize=(12, 12))
# sns.heatmap(data.corr(), square=True, annot=True, ax=ax)
sns.distplot(data['normAmount'], bins=100)
plt.hist(data['normAmount'], bins=50)
plt.plot(data['normAmount'], data['Class'])
plt.scatter(data['V1'], data['V2'])
# 在Class等于0中随机选取500个数据
X = data.iloc[:, data.columns != 'Class']
y = data.iloc[:, data.columns == 'Class']
# 获取类别为0的全部索引
normal_indices = data[data.Class == 0].index
# 类别为1的索引
fraud_indices = np.array(data[data.Class == 1].index)
# 随机选取和类别1一样多的索引
random_normal_indices = np.random.choice(normal_indices, 500, replace=False)
random_normal_indices = np.array(random_normal_indices)
# 合并二者的索引
under_sample_indices = np.concatenate([fraud_indices, random_normal_indices])
# 根据索引获取最终样本数据
under_sample_data = data.iloc[under_sample_indices, :]
# 下采样数据样本
X_undersample = under_sample_data.iloc[:, under_sample_data.columns != 'Class']
y_undersample = under_sample_data.iloc[:, under_sample_data.columns == 'Class']
# 原始数据划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# 下采样后的数据划分
X_train_undersample, X_test_undersample, y_train_undersample, y_test_undersample = train_test_split(X_undersample
, y_undersample
, test_size=0.3
, random_state=0)
# 交叉验证选择最优的参数
def printing_Kfold_scores(x_train_data, y_train_data):
fold = KFold(5, shuffle=False)
fold.get_n_splits(x_train_data)
# Different C parameters
c_param_range = [0.01, 0.1, 1, 10, 100]
results_table = pd.DataFrame(index=range(len(c_param_range), 2), columns=['C_parameter', 'Mean recall score'])
results_table['C_parameter'] = c_param_range
# the k-fold will give 2 lists: train_indices = indices[0], test_indices = indices[1]
j = 0
for c_param in c_param_range:
print('-------------------------------------------')
print('C parameter: ', c_param)
print('-------------------------------------------')
print('')
recall_accs = []
for iteration, indices in fold.split(x_train_data):
# Call the logistic regression model with a certain C parameter
lr = LogisticRegression(C=c_param, penalty='l1', solver='liblinear')
lr.fit(x_train_data.iloc[iteration, :], y_train_data.iloc[iteration, :].values.ravel())
y_pred_undersample = lr.predict(x_train_data.iloc[indices, :].values)
# Calculate the recall score and append it to a list for recall scores representing the current c_parameter
recall_acc = recall_score(y_train_data.iloc[indices, :].values, y_pred_undersample)
recall_accs.append(recall_acc)
print('recall score = ', recall_acc)
# The mean value of those recall scores is the metric we want to save and get hold of.
results_table.loc[j, 'Mean recall score'] = np.mean(recall_accs)
j += 1
print('')
print('Mean recall score ', np.mean(recall_accs))
print('')
best_c = results_table.loc[results_table['Mean recall score'].astype(float).idxmax()]['C_parameter']
# Finally, we can check which C parameter is the best amongst the chosen.
print('*********************************************************************************')
print('Best model to choose from cross validation is with C parameter = ', best_c)
print('*********************************************************************************')
return best_c
# 混淆矩阵
def plot_confusion_matrix(cm, classes,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
"""
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=0)
plt.yticks(tick_marks, classes)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
# 选取最优参数
best_c_1 = printing_Kfold_scores(X_train, y_train)
# 原始数据集建模
lr = LogisticRegression(C=best_c_1, penalty='l1', solver='liblinear')
lr.fit(X_train, y_train.values.ravel())
y_pred = lr.predict(X_test.values)
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test, y_pred)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1, 1] / (cnf_matrix[1, 0] + cnf_matrix[1, 1]))
# Plot non-normalized confusion matrix
class_names = [0, 1]
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_names, title='Confusion matrix')
plt.show()
best_c_2 = printing_Kfold_scores(X_train_undersample, y_train_undersample)
# 下采样后的数据进行建模
lr = LogisticRegression(C=best_c_2, penalty='l1', solver='liblinear')
lr.fit(X_train_undersample, y_train_undersample.values.ravel())
y_pred_undersample = lr.predict(X_test_undersample.values)
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test_undersample, y_pred_undersample)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1, 1] / (cnf_matrix[1, 0] + cnf_matrix[1, 1]))
# Plot non-normalized confusion matrix
class_names = [0, 1]
plt.figure()
plot_confusion_matrix(cnf_matrix
, classes=class_names
, title='Confusion matrix')
plt.show()
数据自取
链接:
百度网盘 请输入提取码
提取码:1234