定义
这个算法可以分为两部分理解,层次与聚类。首先聚类我在另一篇文章有讲过。具体请跳转
【什么是聚类】
。关于层次,就是把数据集聚成很多类以后,然后按照他们的距离构造成一个楼梯形状的簇数据。
层次聚类有两种聚类的方式:
-
Agglomerative – 从下至上的聚类
- 将每一个数据样本作为一个独立的簇。在每一次迭代中将相似的簇合并起来,知道整份数据集结成成一个簇或多个簇
-
Divsive – 从上至下的聚类
- 将所有的数据样本作为一个整体的簇。在每一次迭代中把最不相似的簇分离出整体。最后我们将得到K个簇。
样例
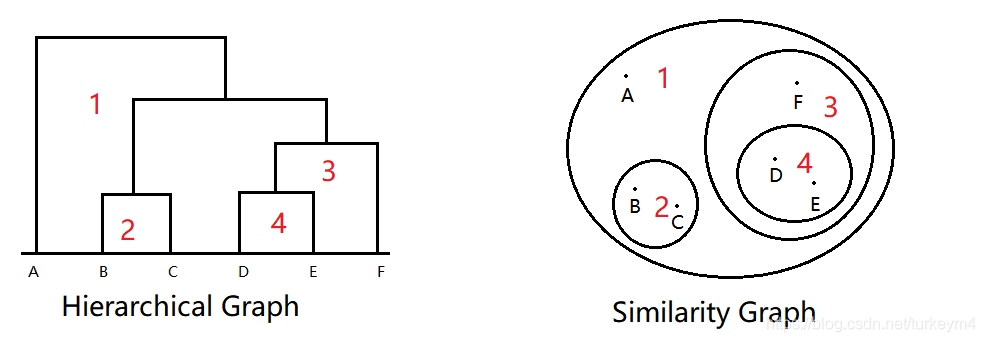
左图是层次图,右图是相似度图,1~4是他们的顺序。从左图我们可以了解到为什么叫层次聚类。对应右图可以看到层次聚类与相似度距离的关系。
- 如果我们使用Agglomerative的方式来进行聚类,那么顺序应该是4->3->2->1
- 如果我们使用Divsive 的方式来进行聚类,那么顺序应该是1->2->3->4
算法
实现层次聚类的算法有很多种。下面我们将学习部分热门的算法。
Single Linkage
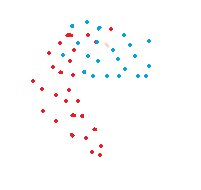
这个算法是以簇之间的最短距离为衡量标准的。
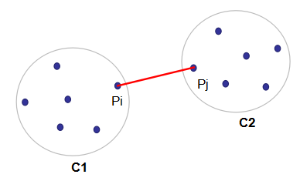
这个算法将以点Pi到点Pj的距离作为簇C1和簇C2的距离。他的object function dist(C1,C2)是:
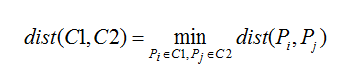
由于它是使用最短距离来计算,所以这个算法只适用于分类明显的数据集。由下图可以看出来,当红点和蓝点交集特别紧密,Single Linkage将很难辨认出噪音。
| 适用 | 不适用 |
|---|---|
|
|
Complete Linkage
这个算法与Single Linkage放好相反。它是以簇之间的最长距离为衡量标准的。
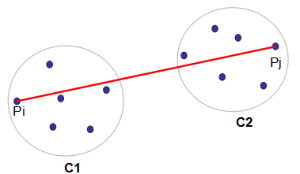
这个算法将以点Pi到点Pj的距离作为簇C1和簇C2的距离。他的object function dist(C1,C2)是:
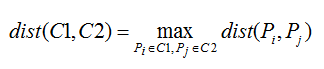
| 适用 | 不适用 |
|---|---|
|
|
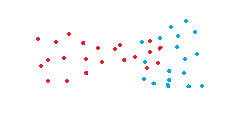
这个算法可以有效识别噪音数据。但有时候它无法识别非椭圆数据。如右图中的红色数据。
Average Linkage
这个算法是计算两个簇之间所有点的距离的平均。可能说的有点拗口,我们看看下图:
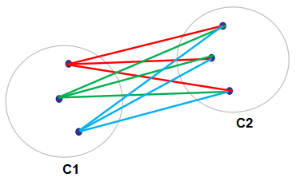
算法会计算C1和C2里3个点的两两距离,然后把他们累加左平均。所以object function dist(C1,C2) 是:
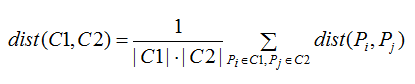
Centroid Linkage
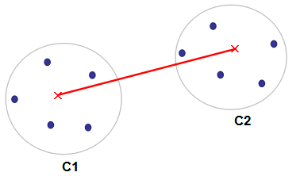
这个算法是计算簇心与簇心的距离。但由于这个算法用的比较少,所以小编选择性学习了。所以就不误导别人了,稍微看看是啥就好,哈哈哈。
Ward
这个算法来源于Joe H. Ward.
Ward在《Hierarchical Grouping To Optimize An Objective Function》这边论文中提出了新的计算距离的方式离差平方和(error sum of squares,ESS)。
什么是离差平方和?
我们先看他们object function长啥样。
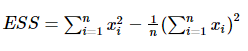
是不是看不懂这个ESS方程怎么出来的?下面这个推导来自于维基百科
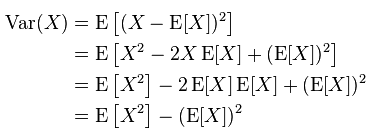
现在是不是非常明白这个object function的整个推导过程了。
怎么使用ESS方程?
- 我们可以将每个点初始化为一个群集。此时,每个群集中的ESS为0
- 计算所有集群的总ESS
- 如果每个群集要合并到新群集中,请计算它们之间的ESS
- 以总ESS值增加最少的方式合并两个集群
- 重复上述步骤,直到所有群集都合并到一个群集中
举个例子,我们有红色簇和蓝色簇以及黑色其他簇
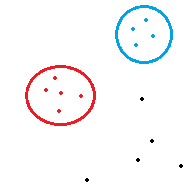
所以合并前后的ESS方程
- ESS(合并前) = ESS(红) + ESS(蓝) +ESS(其他)
- ESS(合并后) = ESS(红&蓝) +ESS(其他)
注意,我们这里没有真正的合并或移动簇,我们仅计算每个簇之间的ESS,并选择ESS(之后)- ESS(之前)中的最小值。不过Ward算法仅适用于欧式距离。
总结
今天我们学习了什么是层次聚类以及层次聚类的常用算法。具体要运用哪一个方式,这个需要大家先对自己的数据集进行分析,然后按照自己的数据特色使用。下期将分享K-Means算法,它属于另外一种聚类算法。
点我阅读更多算法分享