1 量子Fourier变换
离散Fourier变换以一一个复向量
x
0
,
.
.
.
,
x
N
−
1
{x_0},…,{x_{N – 1}}
x
0
,
…
,
x
N
−
1
为输入,输出的数据是如下复向量
y
0
,
.
.
.
,
y
N
−
1
{y_0},…,{y_{N – 1}}
y
0
,
…
,
y
N
−
1
:
y
k
≡
1
N
∑
j
=
0
N
−
1
x
j
e
2
π
i
j
k
/
N
{y_k} \equiv \frac{1}{
{\sqrt N }}\sum\limits_{j = 0}^{N – 1} {
{x_j}{e^{ 2\pi ijk/N}}}
y
k
≡
N
1
j
=
0
∑
N
−
1
x
j
e
2
πijk
/
N
量子Fourier变换是与它严格相同的变换。量子Fourier变换定义为,在一组标准正交基
∣
0
⟩
,
.
.
.
,
∣
N
−
1
⟩
\left| 0 \right\rangle ,…,\left| {N – 1} \right\rangle
∣
0
⟩
,
…
,
∣
N
−
1
⟩
上的一个线性算子,在基态上的作用为
∣
j
⟩
→
1
N
∑
k
=
0
N
−
1
e
2
π
i
j
k
/
N
∣
k
⟩
\left| j \right\rangle \to \frac{1}{
{\sqrt N }}\sum\limits_{k = 0}^{N – 1} {
{e^{2\pi ijk/N}}} \left| k \right\rangle
∣
j
⟩
→
N
1
k
=
0
∑
N
−
1
e
2
πijk
/
N
∣
k
⟩
我们将状态
j
j
j
写成二进制形式
j
=
j
1
j
2
.
.
.
j
n
j=j_1j_2…j_n
j
=
j
1
j
2
…
j
n
,用记号
0.
j
l
j
l
+
1
.
.
.
j
m
0.j_lj_{l+1}…j_m
0.
j
l
j
l
+
1
…
j
m
表示二进制分数。
容易推导出量子Fourier变换的积形式:
∣
j
1
,
.
.
.
,
j
n
⟩
→
1
2
n
/
2
[
(
∣
0
⟩
+
e
2
π
i
0.
j
n
∣
1
⟩
)
(
∣
0
⟩
+
e
2
π
i
0.
j
n
−
1
j
n
∣
1
⟩
)
.
.
.
(
∣
0
⟩
+
e
2
π
i
0.
j
1
.
.
.
j
n
−
1
j
n
∣
1
⟩
)
]
\begin{array}{l} \left| {
{j_1},…,{j_n}} \right\rangle \to \\ \frac{1}{
{
{2^{n/2}}}}\left[ {\left( {\left| 0 \right\rangle + {e^{2\pi i0.{j_n}}}\left| 1 \right\rangle } \right)\left( {\left| 0 \right\rangle + {e^{2\pi i0.{j_{n – 1}}{j_n}}}\left| 1 \right\rangle } \right)…\left( {\left| 0 \right\rangle + {e^{2\pi i0.{j_1}…{j_{n – 1}}{j_n}}}\left| 1 \right\rangle } \right)} \right] \end{array}
∣
j
1
,
…
,
j
n
⟩
→
2
n
/2
1
[
(
∣
0
⟩
+
e
2
πi
0.
j
n
∣
1
⟩
)
(
∣
0
⟩
+
e
2
πi
0.
j
n
−
1
j
n
∣
1
⟩
)
…
(
∣
0
⟩
+
e
2
πi
0.
j
1
…
j
n
−
1
j
n
∣
1
⟩
)
]
量子Fourier变换的有效线路实现如下:
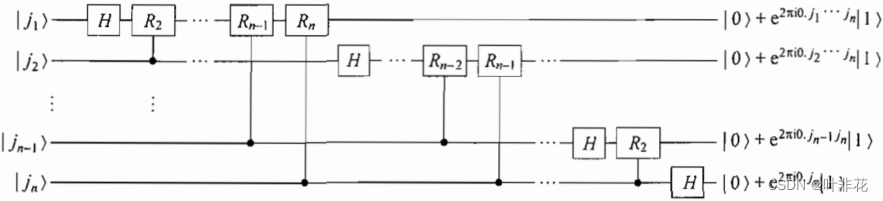
其中门
R
k
R_k
R
k
表示酉变换

使用交换运算逆转量子比特的顺序,量子比特的状态为
1
2
n
/
2
(
∣
0
⟩
+
e
2
π
i
0.
j
n
∣
1
⟩
)
(
∣
0
⟩
+
e
2
π
i
0.
j
n
−
1
j
n
∣
1
⟩
)
.
.
.
(
∣
0
⟩
+
e
2
π
i
0.
j
1
.
.
.
j
n
−
1
j
n
∣
1
⟩
)
\frac{1}{
{
{2^{n/2}}}} {\left( {\left| 0 \right\rangle + {e^{2\pi i0.{j_n}}}\left| 1 \right\rangle } \right)\left( {\left| 0 \right\rangle + {e^{2\pi i0.{j_{n – 1}}{j_n}}}\left| 1 \right\rangle } \right)…\left( {\left| 0 \right\rangle + {e^{2\pi i0.{j_1}…{j_{n – 1}}{j_n}}}\left| 1 \right\rangle } \right)}
2
n
/2
1
(
∣
0
⟩
+
e
2
πi
0.
j
n
∣
1
⟩
)
(
∣
0
⟩
+
e
2
πi
0.
j
n
−
1
j
n
∣
1
⟩
)
…
(
∣
0
⟩
+
e
2
πi
0.
j
1
…
j
n
−
1
j
n
∣
1
⟩
)
量子Fourier变换可使用如下语句实现
from mindquantum.algorithm.library import qft
circ = qft([2,1,0])
circ.svg()

图中的PS门为相位旋转门PhaseShift。

需要注意的是,q0 q1 q2寄存器对应的量子态为
∣
q
2
q
1
q
0
⟩
\left| {
{q_2}{q_1}{q_0}} \right\rangle
∣
q
2
q
1
q
0
⟩
。
2 量子加法器
若有
a
=
a
1
a
2
.
.
.
a
n
a=a_1a_2…a_n
a
=
a
1
a
2
…
a
n
和
b
=
b
1
b
2
.
.
.
b
n
b=b_1b_2…b_n
b
=
b
1
b
2
…
b
n
,欲计算
c
=
a
+
b
c=a+b
c
=
a
+
b
,根据量子Fourier变换的知识,我们可先制备出如下量子态
∣
c
f
⟩
|cf\rangle
∣
c
f
⟩
1
2
n
/
2
(
∣
0
⟩
+
e
2
π
i
0.
c
n
∣
1
⟩
)
(
∣
0
⟩
+
e
2
π
i
0.
c
n
−
1
c
n
∣
1
⟩
)
.
.
.
(
∣
0
⟩
+
e
2
π
i
0.
c
1
.
.
.
c
n
−
1
c
n
∣
1
⟩
)
\frac{1}{
{
{2^{n/2}}}}\left( {\left| 0 \right\rangle + {e^{2\pi i0.{c_n}}}\left| 1 \right\rangle } \right)\left( {\left| 0 \right\rangle + {e^{2\pi i0.{c_{n – 1}}{c_n}}}\left| 1 \right\rangle } \right)…\left( {\left| 0 \right\rangle + {e^{2\pi i0.{c_1}…{c_{n – 1}}{c_n}}}\left| 1 \right\rangle } \right)
2
n
/2
1
(
∣
0
⟩
+
e
2
πi
0.
c
n
∣
1
⟩
)
(
∣
0
⟩
+
e
2
πi
0.
c
n
−
1
c
n
∣
1
⟩
)
…
(
∣
0
⟩
+
e
2
πi
0.
c
1
…
c
n
−
1
c
n
∣
1
⟩
)
再利用逆Fourier变换即可得到
∣
c
1
c
2
.
.
.
c
n
⟩
|c_1c_2…c_n\rangle
∣
c
1
c
2
…
c
n
⟩
。
2.1 不考虑最高位进位
观察到



于是可使用如下线路制备
∣
c
f
⟩
|cf\rangle
∣
c
f
⟩
,这里先不考虑最高位有进位的情况。
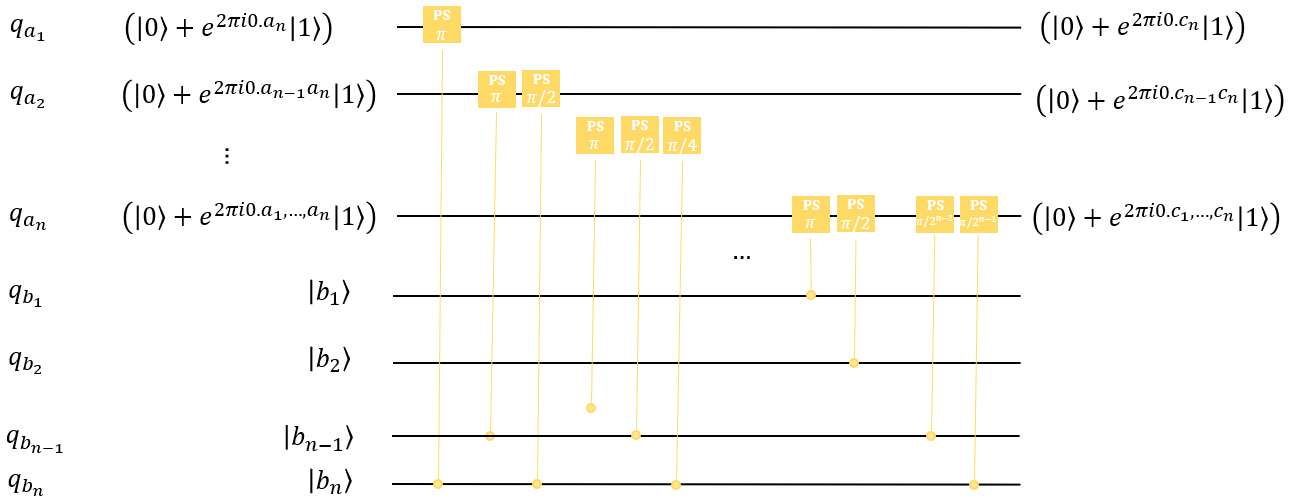
将这个线路记作MAdder(Modular Adder)。于是,量子加法器的线路如下(不考虑最高位进位):

2.2 考虑最高位进位
考虑
a
=
a
1
a
2
.
.
.
a
n
a=a_1a_2…a_n
a
=
a
1
a
2
…
a
n
,
b
=
b
1
b
2
.
.
.
b
n
b=b_1b_2…b_n
b
=
b
1
b
2
…
b
n
,
c
=
a
+
b
=
c
1
c
2
.
.
.
c
n
+
1
c = a + b = {c_1}{c_2}…{c_{n + 1}}
c
=
a
+
b
=
c
1
c
2
…
c
n
+
1
。
c
1
=
0
c_1=0
c
1
=
0
表示最高位无进位,
c
1
=
1
c_1=1
c
1
=
1
表示最高位有进位。
若考虑最高位进位,则需要给
a
a
a
增加一个量子比特存储进位项。
∣
a
⟩
=
∣
0
a
1
,
.
.
.
,
a
n
⟩
\left|a \right\rangle = \left| {0{a_1},…,{a_n}} \right\rangle
∣
a
⟩
=
∣
0
a
1
,
…
,
a
n
⟩
对
∣
a
⟩
\left|a \right\rangle
∣
a
⟩
做量子Fourier变换后

观察到

于是制备
∣
c
f
⟩
|cf\rangle
∣
c
f
⟩
的线路如下
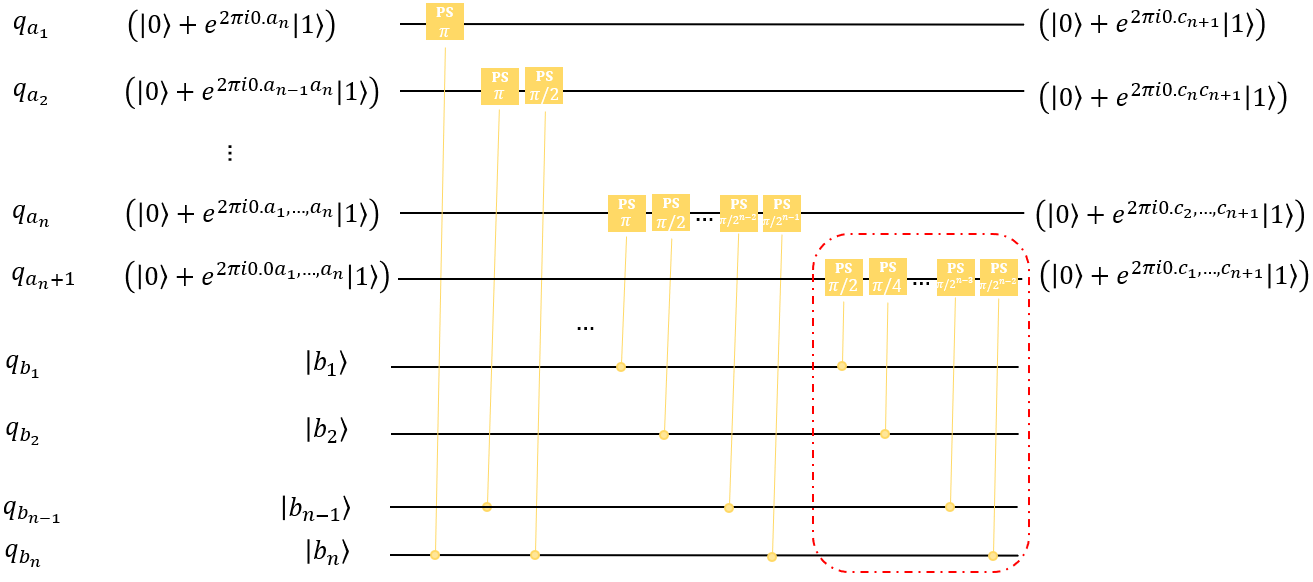
注意:红框里线路的旋转角相比于前面的线路均多除了一个2。
将上图线路记作Adder,完整的量子加法器线路如下

3 代码实现
导入一些用到的包
from mindquantum.algorithm.library import qft
from mindquantum.simulator import Simulator
from mindquantum.core.gates import X, PhaseShift
from mindquantum.core.circuit import Circuit,dagger
import numpy as np
定义受控相位旋转操作
def _rn(k):
return PhaseShift(2 * np.pi / 2 ** k)
def C_R(tq, cq, k):
circ = Circuit()
circ += _rn(k).on(tq, cq)
return circ
定义adder,这里考虑了进位项
def m_adder(qa, qb):
circ = Circuit()
qa_num = len(qa)
qb_num = len(qb)
for q in range(qb_num):
for i in range(qb_num - q - 1, qb_num):
circ += C_R(qa[qa_num - q - 1], qb[qb_num - i - 1], i - (qb_num - q - 1) + 1)
if qa_num > qb_num and q == (qb_num - 1): # 进位的控制
for i in range(qb_num - q - 1, qb_num):
circ += C_R(qa[qa_num - q - 1 - 1], qb[qb_num - i - 1], i - (qb_num - q - 1) + 1 + 1)
return circ
输入a和b的值(假设a,b都是3bit二进制数),并执行加法器
#定义存储a和b的寄存器qa,qb
qa = [3, 4, 5, 6]
qb = [0, 1, 2]
circ = Circuit()
# qa 输入a的值 001
# circ += X.on(5)
# circ += X.on(4)
circ += X.on(3)
# qb 输入b的值 111
circ += X.on(2)
circ += X.on(1)
circ += X.on(0)
#对qa执行量子Fourier操作
circ += qft([6, 5, 4, 3])
#执行加法操作
adder = m_adder(qa, qb)
circ += adder
#使用量子逆Four变换恢复出结果
circ += dagger(qft([6, 5, 4, 3]))
sim = Simulator('projectq', 7)
sim.apply_circuit(circ)
print(sim.get_qs(True))
circ.svg() #查看整个线路
1¦1000111⟩
结果保存在qa寄存器中即c=1000
qb寄存器中值不变,即b=111
附:无进位加法器完整代码
from mindquantum import Circuit, UN, H, Z
from mindquantum.algorithm.library import amplitude_encoder,qft
from mindquantum.simulator import Simulator
from mindquantum.core.gates import T, H, X, Power, BARRIER,SWAP,PhaseShift
from mindquantum.core.circuit import Circuit, UN
from mindquantum.core.circuit import controlled
from mindquantum.core.circuit import dagger
import numpy as np
from mindquantum.core.gates import Measure
def _rn(k):
return PhaseShift(2 * np.pi / 2**k)
def C_R(tq, cq, k):
circ = Circuit()
circ += _rn(k).on(tq, cq)
return circ
def m_adder(qa,qb):
circ = Circuit()
qa_num = len(qa)
qb_num = len(qb)
for q in range(qb_num):
#无进位
for i in range(qb_num-q-1,qb_num):
circ += C_R(qa[qa_num-q-1], qb[qb_num-i-1], i-(qb_num-q-1)+1)
return circ
qa = [3,4,5]
qb = [0,1,2]
cc = m_adder(qa,qb)
circ = Circuit()
#qa
# circ += X.on(5)
# circ += X.on(4)
circ += X.on(3)
#qb
circ += X.on(2)
circ += X.on(1)
circ += X.on(0)
circ += qft([5,4,3])
circ += cc
circ += dagger(qft([5,4,3]))
sim = Simulator('projectq', 6)
sim.apply_circuit(circ)
print(sim.get_qs(True))
circ.svg()
#基于qft的加法,结果保存到qa寄存器
#quantum adder based on Fourier Transform
参考资料
[1] Engin Şahin. Quantum arithmetic operations based on quantum fourier transform on signed integers. International Journal of Quantum Information. (2020) 2050035 (21 pages).