机器学习与计算机视觉入门项目——视频投篮检测(三)
在第二部分,我记录了实验中提取图像特征的HOG算子及其实现代码,我们接下来就要构造几个简单的分类器,对数据集的HOG特征来分类,实现进球/不进球的分类任务。
分类器的设计和选择
实验中要用到的分类模型主要有四个:
- logistic回归
- SVM支持向量机
- MLP多层感知机
- CNN卷积神经网络
构建分类器的过程中总有许多因素会对最终性能产生影响,比如数据的增广方式、模型的超参数、是否引入某个修正项等等。不同因素的组合会产生非常多的可选方案,因此我们采用
交叉验证
和绘制
ROC曲线
的形式来确定模型的最优超参数,并比较不同参数及不同模型的优劣。
交叉验证
和
ROC曲线
在随后都会讲到。
几种损失函数
| 函数名称 | 形式 |
|---|---|
| 均方误差损失 |
M S E = − 1 n ∑ i = 1 n ( y ^ i − y i ) 2 MSE=-\frac{1}{n} \sum_{i=1}^{n} (\widehat{y}_{i}-y_i)^2 M S E = − n 1 i = 1 ∑ n ( y i − y i ) 2 y i y_i y i 是数据的真实标签, y ^ i \widehat{y}_i y i 是模型的输出结果 |
| 平均交叉熵损失 |
− 1 m [ ∑ i = 1 m ∑ j = 0 1
1 { y ( i ) = j }
l o g
p ( y ( i ) = j ∣ x ( i ) ; θ ) ] -\frac{1}{m}[\sum_{i=1}^{m}\sum_{j=0}^{1}\ 1\{ y^{(i)}=j\}\ log \ p(y^{(i)}=j\mid x^{(i)};\theta)] − m 1 [ i = 1 ∑ m j = 0 ∑ 1 1 { y ( i ) = j } l o g p ( y ( i ) = j ∣ x ( i ) ; θ ) ] 1 { ⋅ } 1\{ \cdot \} 1 { ⋅ } 是指示函数,当 y ( i ) = j y^{(i)}=j y ( i ) = j 时函数值为1否则为0 |
|
0 − 1 0-1 0 − 1 损失 |
L 0 , 1 = ∑ i = 0 m
I f ( x ( i ) ) ≠ y ( i ) L_{0,1}=\sum_{i=0}^{m}\ I_{f(x^{(i)})\ne y^{(i)}} L 0 , 1 = i = 0 ∑ m I f ( x ( i ) ) ̸ = y ( i ) I x I_x I x 也是指示函数,0-1损失相当于记录了模型分类出错的次数 |
| 负对数似然损失 |
N L L ( θ , D ) = − ∑ i = 0 ∣ D ∣
l o g
P ( Y = y ( i ) ∣ x ( i ) , θ ) NLL(\theta,D)=-\sum_{i=0}^{\mid D \mid}\ log\ P(Y=y^{(i)}\mid x^{(i)},\theta) N L L ( θ , D ) = − i = 0 ∑ ∣ D ∣ l o g P ( Y = y ( i ) ∣ x ( i ) , θ ) |
|
L 1 L1 L 1 正则化 |
E ( θ , D ) = N L L ( θ , D ) + λ ∣ ∣ θ ∣ ∣ 1 E(\theta,D)=NLL(\theta,D)+\lambda\mid \mid \theta \mid \mid_1 E ( θ , D ) = N L L ( θ , D ) + λ ∣ ∣ θ ∣ ∣ 1 ∣ ∣ θ ∣ ∣ p = ( ∑ j = 0 ∣ θ ∣
∣ θ j ∣ p ) 1 p p = 1 \mid \mid \theta \mid \mid_p=(\sum_{j=0}^{\mid \theta\mid}\ \mid \theta_j \mid^p)^{\frac{1}{p}} \quad p=1 ∣ ∣ θ ∣ ∣ p = ( j = 0 ∑ ∣ θ ∣ ∣ θ j ∣ p ) p 1 p = 1 |
|
L 2 L2 L 2 正则化 |
E ( θ , D ) = N L L ( θ , D ) + λ ∣ ∣ θ ∣ ∣ 2 E(\theta,D)=NLL(\theta,D)+\lambda\mid \mid \theta \mid \mid_2 E ( θ , D ) = N L L ( θ , D ) + λ ∣ ∣ θ ∣ ∣ 2 ∣ ∣ θ ∣ ∣ p = ( ∑ j = 0 ∣ θ ∣
∣ θ j ∣ p ) 1 p p = 2 \mid \mid \theta \mid \mid_p=(\sum_{j=0}^{\mid \theta\mid}\ \mid \theta_j \mid^p)^{\frac{1}{p}} \quad p=2 ∣ ∣ θ ∣ ∣ p = ( j = 0 ∑ ∣ θ ∣ ∣ θ j ∣ p ) p 1 p = 2 |
我所理解的正则化的一个目的是限制
θ
\theta
θ
的各维分量不至于出现极大的值,也就是避免出现输入向量中某一维度
Logistic回归
基本原理
logistic回归是一个基于概率的线性二分类器,通过学习一组权重向量
ω
\omega
ω
和偏置
b
b
b
,模型将一个输入向量映射到一个高维空间。权重可以理解为对输入特征向量的线性加权,体现了不同维度对分类的重要程度,偏置可以理解为系统的零输入响应,是系统在没有输入的情况下的输出值。
x
→
ω
T
x
+
b
x\to \omega^Tx+b
x
→
ω
T
x
+
b
实际上,模型的参数
ω
\omega
ω
和
b
b
b
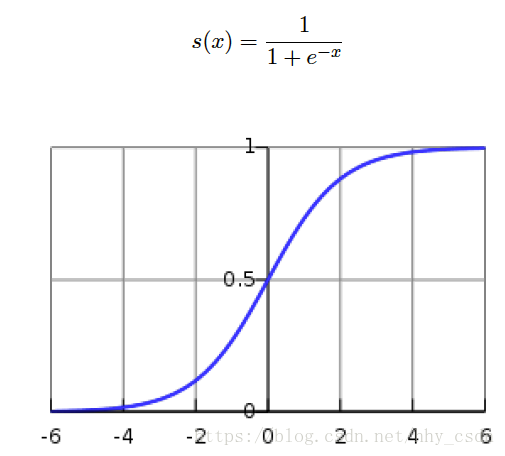
正是决定了这个高维空间中的一个超平面,用于将样本点分在超平面的两侧。而下面的公式也可以说明,样本点距离超平面的距离与属于该类别的概率成正比。
s
(
x
)
=
1
1
+
e
−
(
ω
T
x
+
b
)
s(x)=\frac{1}{1+e^{-(\omega^T x+b)}}
s
(
x
)
=
1
+
e
−
(
ω
T
x
+
b
)
1
P
(
y
=
1
∣
x
′
θ
)
=
1
1
+
e
−
(
ω
T
x
+
b
)
P(y=1|x'\theta)=\frac{1}{1+e^{-(\omega^Tx+b)}}
P
(
y
=
1
∣
x
′
θ
)
=
1
+
e
−
(
ω
T
x
+
b
)
1
我们将输入向量稍作改动,添加一个常数1的维度,目的是将偏置
b
b
b
写进输入向量
x
x
x
,同时将权重
ω
\omega
ω
增加一维,用于和
x
′
x'
x
′
的最后一维相乘,得到偏置。
ω
T
x
+
b
=
θ
T
x
′
\omega^Tx+b=\theta^T x'
ω
T
x
+
b
=
θ
T
x
′
那么上两式就可以改写成
s
(
x
)
=
1
1
+
e
−
θ
T
x
′
s(x)=\frac{1}{1+e^{-\theta^Tx'}}
s
(
x
)
=
1
+
e
−
θ
T
x
′
1
P
(
y
=
1
∣
x
′
θ
)
=
1
1
+
e
−
θ
T
x
′
P(y=1|x'\theta)=\frac{1}{1+e^{-\theta^Tx'}}
P
(
y
=
1
∣
x
′
θ
)
=
1
+
e
−
θ
T
x
′
1
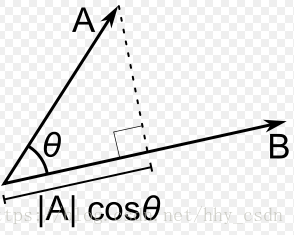
其中,
θ
T
x
′
\theta^Tx'
θ
T
x
′
是高维空间中一点到由
θ
\theta
θ
决定的超平面的距离,因为
θ
T
x
′
=
θ
⃗
⋅
x
⃗
\theta^Tx'=\vec \theta \cdot \vec x
θ
T
x
′
=
θ
⋅
x
,默认向量都是列向量,
θ
\theta
θ
规定为超平面的法向量,它可以朝向平面任一侧。距离越大,向量点积的值就越大,根据
s
i
g
m
o
i
d
sigmoid
s
i
g
m
o
i
d
函数的图像我们知道该点属于某一类别的概率值就越接近于1,相反如果数据点在法向量
θ
\theta
θ
的另一侧,其点积的值越接近
−
1
-1
−
1
,属于另一类的概率就越大。
损失函数
在二值分类的问题中,我们将平均交叉熵损失函数写成如下
J
(
θ
)
=
−
1
m
[
∑
i
=
1
m
y
(
i
)
l
o
g
h
θ
(
x
(
i
)
)
+
(
1
−
y
(
i
)
)
l
o
g
(
1
−
h
θ
(
x
(
i
)
)
)
]
+
λ
∣
∣
θ
∣
∣
2
2
J(\theta)=-\frac{1}{m}[\sum_{i=1}^{m}y^{(i)}\ log\ h_\theta(x^{(i)})+(1-y^{(i)})log\ (1-h_\theta(x^{(i)}))]+\lambda\mid \mid \theta \mid\mid ^2_2
J
(
θ
)
=
−
m
1
[
i
=
1
∑
m
y
(
i
)
l
o
g
h
θ
(
x
(
i
)
)
+
(
1
−
y
(
i
)
)
l
o
g
(
1
−
h
θ
(
x
(
i
)
)
)
]
+
λ
∣
∣
θ
∣
∣
2
2
其中,
h
θ
(
x
(
i
)
)
=
1
1
+
e
−
θ
T
x
(
i
)
′
h_\theta(x^{(i)})=\frac{1}{1+e^{-\theta^Tx^{(i)'}}}
h
θ
(
x
(
i
)
)
=
1
+
e
−
θ
T
x
(
i
)
′
1
,
x
(
i
)
x^{(i)}
x
(
i
)
是数据集中第
i
i
i
个样本,这个损失函数也就是Logistic回归的损失函数。下面我们用梯度下降法对它进行求解。
Logistic回归的求解——梯度下降法
直接将梯度下降的算法写出来。
1.
置
迭
代
代
数
k
=
0
,
设
置
初
始
点
x
0
置迭代代数k=0,设置初始点\bm{x_0}
置
迭
代
代
数
k
=
0
,
设
置
初
始
点
x
0
2.
重
复
以
下
操
作
重复以下操作
重
复
以
下
操
作
3.
计
算
下
降
方
向
P
k
\quad \quad \quad计算下降方向\bm{P_k}
计
算
下
降
方
向
P
k
1
4.
选
择
α
k
∈
ℜ
+
作
为
下
降
步
长
“
尽
量
”
最
小
化
h
(
α
)
=
f
(
x
k
+
α
P
k
)
\quad \quad \quad选择\alpha_k\in \Re_+作为下降步长“尽量”最小化h(\alpha)=f(\bm{x_k}+\alpha\bm{P_k})
选
择
α
k
∈
ℜ
+
作
为
下
降
步
长
“
尽
量
”
最
小
化
h
(
α
)
=
f
(
x
k
+
α
P
k
)
2
5.
用
步
长
α
k
来
更
新
当
前
点
x
k
,
x
k
+
1
=
x
k
+
α
k
P
k
,
k
=
k
+
1
\quad \quad \quad用步长\alpha_k来更新当前点\bm{x_k},\bm{x_{k+1}=\bm{x_k+\alpha_kP_k}},k=k+1
用
步
长
α
k
来
更
新
当
前
点
x
k
,
x
k
+
1
=
x
k
+
α
k
P
k
,
k
=
k
+
1
6.
当
∣
∣
∇
f
(
x
k
)
<
ϵ
时
算
法
停
止
当\mid \mid \nabla f(\bm{x_k})<\epsilon时算法停止
当
∣
∣
∇
f
(
x
k
)
<
ϵ
时
算
法
停
止
损失函数的梯度计算
补充的向量微分知识。

我们将要对这个函数求梯度向量。
J
(
θ
)
=
−
1
m
[
∑
i
=
1
m
y
(
i
)
l
o
g
h
θ
(
x
(
i
)
)
+
(
1
−
y
(
i
)
)
l
o
g
(
1
−
h
θ
(
x
(
i
)
)
)
]
+
λ
∣
∣
θ
∣
∣
2
2
J(\theta)=-\frac{1}{m}[\sum_{i=1}^{m}y^{(i)}\ log\ h_\theta(x^{(i)})+(1-y^{(i)})log\ (1-h_\theta(x^{(i)}))]+\lambda\mid \mid \theta \mid\mid ^2_2
J
(
θ
)
=
−
m
1
[
i
=
1
∑
m
y
(
i
)
l
o
g
h
θ
(
x
(
i
)
)
+
(
1
−
y
(
i
)
)
l
o
g
(
1
−
h
θ
(
x
(
i
)
)
)
]
+
λ
∣
∣
θ
∣
∣
2
2
∵
h
θ
(
x
)
=
1
1
+
e
−
θ
T
x
,
x
,
θ
是
向
量
\because h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}, x,\theta是向量
∵
h
θ
(
x
)
=
1
+
e
−
θ
T
x
1
,
x
,
θ
是
向
量
d
h
(
x
)
d
x
=
h
(
x
)
[
1
−
h
(
x
)
]
\frac{dh(x)}{dx}=h(x)[1-h(x)]
d
x
d
h
(
x
)
=
h
(
x
)
[
1
−
h
(
x
)
]
∴
∂
h
θ
(
x
)
∂
θ
=
∂
h
θ
(
x
)
∂
(
θ
T
x
)
∂
(
θ
T
x
)
∂
θ
=
h
θ
(
1
−
h
θ
)
x
T
\therefore \frac{\partial h_\theta(x)}{\partial \theta}=\frac{\partial h_\theta(x)}{\partial(\theta^Tx)}\frac{\partial (\theta^Tx)}{\partial \theta}=h_\theta(1-h_\theta)x^T
∴
∂
θ
∂
h
θ
(
x
)
=
∂
(
θ
T
x
)
∂
h
θ
(
x
)
∂
θ
∂
(
θ
T
x
)
=
h
θ
(
1
−
h
θ
)
x
T
∴
∇
θ
J
(
θ
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
1
h
θ
∂
h
θ
∂
θ
+
(
1
−
y
(
i
)
)
1
1
−
h
θ
(
−
1
)
∂
h
θ
∂
θ
]
+
λ
θ
T
\therefore \nabla_\theta J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}\frac{1}{h_\theta}\frac{\partial h_\theta}{\partial \theta}+(1-y^{(i)})\frac{1}{1-h_\theta}(-1)\frac{\partial h_\theta}{\partial \theta}]+\lambda\theta^T
∴
∇
θ
J
(
θ
)
=
−
m
1
i
=
1
∑
m
[
y
(
i
)
h
θ
1
∂
θ
∂
h
θ
+
(
1
−
y
(
i
)
)
1
−
h
θ
1
(
−
1
)
∂
θ
∂
h
θ
]
+
λ
θ
T
∴
∇
θ
J
(
θ
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
1
h
θ
h
θ
(
1
−
h
θ
)
x
(
i
)
T
+
(
y
(
i
)
−
1
)
1
1
−
h
θ
h
θ
(
1
−
h
θ
)
x
(
i
)
T
]
+
λ
θ
T
\therefore \nabla_\theta J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}\frac{1}{h_\theta}h_\theta(1-h_\theta)x^{(i)T}+(y^{(i)}-1)\frac{1}{1-h_\theta}h_\theta(1-h_\theta)x^{(i)T}]+\lambda\theta^T
∴
∇
θ
J
(
θ
)
=
−
m
1
i
=
1
∑
m
[
y
(
i
)
h
θ
1
h
θ
(
1
−
h
θ
)
x
(
i
)
T
+
(
y
(
i
)
−
1
)
1
−
h
θ
1
h
θ
(
1
−
h
θ
)
x
(
i
)
T
]
+
λ
θ
T
∴
∇
θ
J
(
θ
)
=
−
1
m
∑
i
=
1
m
x
(
i
)
T
[
y
(
i
)
(
1
−
h
θ
)
+
(
y
(
i
)
−
1
)
h
θ
]
+
λ
θ
T
\therefore \nabla_\theta J(\theta)=-\frac{1}{m} \sum_{i=1}^{m} x^{(i)T} [ y^{(i)} (1-h_\theta)+(y^{(i)}-1) h_\theta]+\lambda\theta^T
∴
∇
θ
J
(
θ
)
=
−
m
1
i
=
1
∑
m
x
(
i
)
T
[
y
(
i
)
(
1
−
h
θ
)
+
(
y
(
i
)
−
1
)
h
θ
]
+
λ
θ
T
∴
∇
θ
J
(
θ
)
=
−
1
m
∑
i
=
1
m
x
(
i
)
T
(
y
(
i
)
−
h
θ
)
+
λ
θ
T
\therefore \nabla_\theta J(\theta)=-\frac{1}{m} \sum_{i=1}^{m} x^{(i)T}(y^{(i)}-h_\theta)+\lambda\theta^T
∴
∇
θ
J
(
θ
)
=
−
m
1
i
=
1
∑
m
x
(
i
)
T
(
y
(
i
)
−
h
θ
)
+
λ
θ
T
上式就是损失函数关于权重向量
θ
\theta
θ
的梯度向量,应该是一个行向量