展开全部
各类三角形求面积方式如下所示:
1.已知e69da5e6ba9062616964757a686964616f31333365666264三角形底a,高h,则 S=ah/2
2.已知三角形三边a,b,c,则
(海伦公式)(p=(a+b+c)/2)
S=sqrt[p(p-a)(p-b)(p-c)]
=sqrt[(1/16)(a+b+c)(a+b-c)(a+c-b)(b+c-a)]
=1/4sqrt[(a+b+c)(a+b-c)(a+c-b)(b+c-a)]
3.已知三角形两边a,b,这两边夹角C,则S=1/2
absinC,即两夹边之积乘夹角的正弦值。
4.设三角形三边分别为a、b、c,内切圆半径为r
则三角形面积=(a+b+c)r/2
5.设三角形三边分别为a、b、c,外接圆半径为R
则三角形面积=abc/4R
6.行列式形式
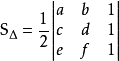
为三阶行列式,此三角形
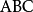
在平面直角坐标系内
,这里
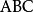
选取最好按逆时针顺序从右上角开始取,因为这样取得出的结果一般都为正值,如果不按这个规则取,可能会得到负值,但不要紧,只要取绝对值就可以了,不会影响三角形面积的大小。
该公式的证明可以借助“两夹边之积乘夹角的正弦值”的面积公式 。
7.海伦——秦九韶三角形中线面积公式:
S=√[(Ma+Mb+Mc)*(Mb+Mc-Ma)*(Mc+Ma-Mb)*(Ma+Mb-Mc)]/3
其中Ma,Mb,Mc为三角形的中线长.
8.根据三角函数求面积:
S= ½ab sinC=2R² sinAsinBsinC= a²sinBsinC/2sinA
注:其中R为外切圆半径。
9.根据向量求面积:
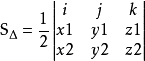
其中,(x1,y1,z1)与(x2,y2,z2)分别为向量AB与AC在空间直角坐标系下的坐标表达,即:
向量临边构成三角形面积等于向量临边构成平行四边形面积的一半。
扩展资料
三角形面积公式是指使用算式计算出三角形的面积,同一平面内,且不在同一直线的三条线段首尾顺次相接所组成的封闭图形叫做三角形,符号为△。
常见的三角形按边分有等腰三角形(腰与底不等的等腰三角形、腰与底相等的等腰三角形即等边三角形)、不等腰三角形;按角分有直角三角形、锐角三角形、钝角三角形等,其中锐角三角形和钝角三角形统称斜三角形。