原始Gan Loss
m
i
n
G
m
a
x
D
V
(
D
,
G
)
=
E
x
∼
P
d
a
t
a
[
l
o
g
D
(
x
)
]
+
E
z
∼
P
z
(
Z
)
[
l
o
g
(
1
−
D
(
G
(
Z
)
)
)
]
\mathop{min}\limits_{G}\space \mathop{max}\limits_{D}\space V(D,G) = E_{x\sim P_{data}}[log\space D(x)] + E_{z \sim P_z \space (Z)}[log(1-D(G(Z)))]
G
min
D
ma
x
V
(
D
,
G
)
=
E
x
∼
P
d
a
t
a
[
l
o
g
D
(
x
)]
+
E
z
∼
P
z
(
Z
)
[
l
o
g
(
1
−
D
(
G
(
Z
)))]
该Loss的目标是同时优化两个对立的目标,即maximize V(D)和minimize V(G).
首先,最大化V(D)时,函数图像分别为
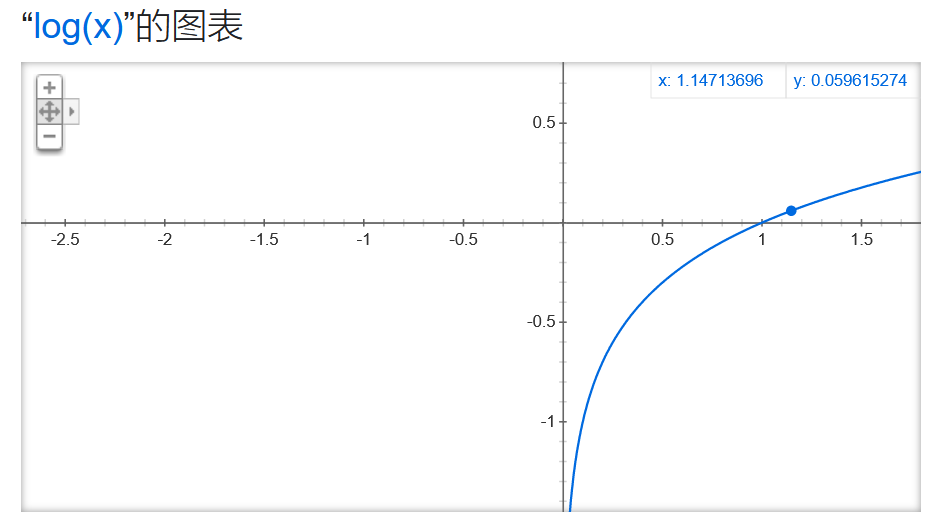
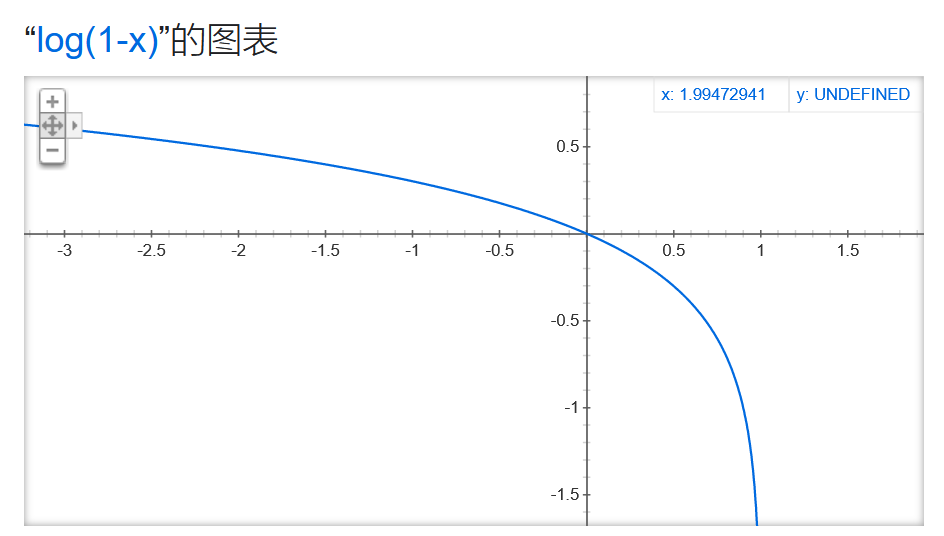
因此,要想
最大化V(D),只需要D(x) → 1,D(G(Z)) → 0
(注: 原始GAN Loss中判别器D 的输出需要经过Sigmoid 的函数,故其输出的值为 0 ~ 1) 即可,即使得对于真实图像Discriminator的输出概率D(x)趋近于1,而对于生成的图像Discriminator的输出概率接近于0,便可实现最大化V(D)从而优化判别器的目的。
其次,要优化Generator,便要最小化 V(G),由于公式的中第一项
E
x
∼
P
d
a
t
a
[
l
o
g
D
(
x
)
]
E_{x\sim P_{data}}[log\space D(x)]
E
x
∼
P
d
a
t
a
[
l
o
g
D
(
x
)]
不含G,因此只需最小化
E
z
∼
P
z
(
Z
)
[
l
o
g
(
1
−
D
(
G
(
Z
)
)
)
E_{z \sim P_z \space (Z)}[log(1-D(G(Z)))
E
z
∼
P
z
(
Z
)
[
l
o
g
(
1
−
D
(
G
(
Z
)))
即可,由函数图像可知,
最小化 V(G)只需要让D(G(Z)) →1即可
。分别训练生成器和判别器一段时间,再联合进行训练,即可实现Gan网络的优化过程。
Hinge Gan Loss
Hinge Gan Loss是Hinge Loss 和传统 Gan Loss的一个结合,首先理解Hinge Loss.
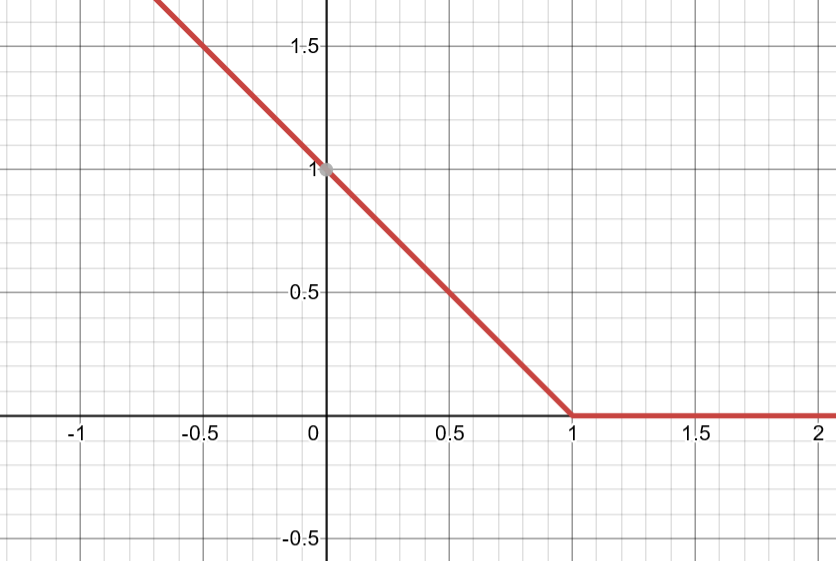
H
i
n
g
e
L
o
s
s
=
m
a
x
(
0
,
1
−
t
y
)
Hinge Loss = max(0, 1- ty)
H
in
g
e
L
oss
=
ma
x
(
0
,
1
−
t
y
)
的图像如上图所示,
t
y
≧
1
ty \geqq 1
t
y
≧
1
的部分都变为了0 ,其中
t
t
t
表示期望的输出标签
±
1
\pm 1
±
1
,而y 表示SVM的直接输出如
y
=
w
∗
x
+
b
y = w*x + b
y
=
w
∗
x
+
b
。也可以用以下公式进行表示:
H
i
n
g
e
L
o
s
s
=
{
1
−
t
y
,
i
f
t
y
<
1
0
,
o
t
h
e
r
w
i
s
e
Hinge Loss = \begin{cases} 1- ty \hspace{2em} ,if \hspace{1em} ty<1 \\0 \hspace{4em},otherwise\end{cases}
H
in
g
e
L
oss
=
{
1
−
t
y
,
i
f
t
y
<
1
0
,
o
t
h
er
w
i
se
以上公式的含义是,如果预测的标签是正确的(即t 与 y 同号), 且
∣
y
∣
\vert{y}\vert
∣
y
∣
>1 时,loss为 0
若预测的标签是错误的(即t 与 y 异号),则loss 随着 y 线性增长。类似的,当
∣
y
∣
\vert{y}\vert
∣
y
∣
<1时,即使 t 与y 同号(分类正确),但还是会因为间距不足仍然产生损失。
Hinge Loss 变种
Hinge Loss还有以下变种:
L
(
y
,
y
^
)
=
m
a
x
(
0
,
m
−
y
+
y
^
)
L(y,\hat y) = max(0,m-y+\hat y)
L
(
y
,
y
^
)
=
ma
x
(
0
,
m
−
y
+
y
^
)
其中:
y
y
y
表示正(真实)样本得分,
y
^
\hat y
y
^
表示 负(预测)样本得分,m表示正负样本的最小间距(margin).
Hinge Loss的目标是尽力拉大正负样本的得分差距,在以上变种中正负样本的的得分间距最小要满足margin条件(
假设在一个分类问题中,机器什么也没学到,对于每个类都给出一样的分数,这个时候margin的存在就有作用了,使得loss至少是m, 而不至于是0
)。
Hinge Gan Loss
V
(
D
,
G
)
=
L
D
+
L
G
V(D,G) = L_D + L_G
V
(
D
,
G
)
=
L
D
+
L
G
L
D
=
E
[
m
a
x
(
0
,
1
−
D
(
x
)
)
]
+
E
[
m
a
x
(
0
,
1
+
D
(
G
(
z
)
)
)
]
L_D = E[max(0,1-D(x))] + E[max(0,1+D(G(z)))]
L
D
=
E
[
ma
x
(
0
,
1
−
D
(
x
))]
+
E
[
ma
x
(
0
,
1
+
D
(
G
(
z
)))]
优化目标: D(x) → 1,D(G(z)) → -1
对于判别器来说,只有
D
(
x
)
<
1
D(x)<1
D
(
x
)
<
1
(真实样本的概率小于1)和
D
(
G
(
z
)
)
>
−
1
D(G(z))> -1
D
(
G
(
z
))
>
−
1
(伪造样本的概率大于0)这两种情况会产生loss,需要被优化,其余情况loss为0,从而一定程度上稳定了判别器的训练。
L
G
=
−
E
[
D
(
G
(
z
)
)
]
L_{G} = -E[D(G(z))]
L
G
=
−
E
[
D
(
G
(
z
))]
优化目标: D(G(z)) → 1
参考
https://zh.wikipedia.org/zh-cn/Hinge_loss
https://zhuanlan.zhihu.com/p/72195907