题目描述
公司有编号为 1 到 n 的 n 个工程师,给你两个数组 speed 和 efficiency ,其中 speed[i] 和 efficiency[i] 分别代表第 i 位工程师的速度和效率。请你返回由最多 k 个工程师组成的 最大团队表现值 ,由于答案可能很大,请你返回结果对 10^9 + 7 取余后的结果。
团队表现值的定义为:一个团队中「所有工程师速度的和」乘以他们「效率值中的最小值」。
力扣:1383. 最大的团队表现值
输入:n = 6 , speed = [2 , 10 , 3 , 1 , 5 , 8], efficiency = [5 , 4 , 3 , 9 , 7 , 2 ] , k = 3
输出:68
解释:此示例与第一个示例相同,除了 k = 3 。我们可以选择工程师 1 ,工程师 2 和工程师 5 得到最大的团队表现值。表现值为 performance = (2 + 10 + 5) * min(5, 4, 7) = 68 。
题目分析
题目的意思很简单,团队表现值 = 「所有工程师速度的和」乘以「效率值中的最小值」, 使得团对表现值尽可能的大 。
1、 首先需要考虑的是,如何维护从 k 名中获取最小的效率 minE ?
针对这个为题,可以考虑采用
滑动窗口
,先按照 efficiency 降序,那么此时每次窗口更新后,
新添加进来的员工,即为当前 k 名员工中具有最小效率 minE
。

2、其次需要考虑的是,如何维护 k 名员工
速度和
最大化 ?
上面已经提到了
新添加的员工具有 minE 的特性
,既然有新添加的,即需要从前 k 名中移除一名员工 , 那么哪名员工需要被移出呢 ?考虑到需要维护
k 名员工速度和最大
, 很容易想到
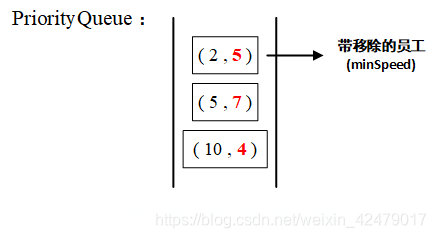
移除当前滑动窗口中 k 名员工速度最小的那名员工,由新员工替换。
考虑到这里需要维护 k 名员工按照速度的升序的集合, 优先队列 PriorityQueue 很符合这里的使用。
3、 上面提到了对速度和效率的排序,题目中给的是两个数组,一旦排序就会使得两个数组的的配对关系混乱,所以先需要构建一个员工对象来保存员工的速度的效率即可。
AC代码
class Solution {
// 构建一个员工对象,此题需要对其属性进行排序,而一旦排序两个数组的关系会被打乱
class Staff{
int s , e;
public Staff(int s , int e){
this.s = s;
this.e = e;
}
}
public int maxPerformance(int n, int[] speed, int[] efficiency, int k) {
final int MOD = 1000000007;
// 1. 首先构建员工对象
List<Staff> list = new ArrayList<>();
for(int i = 0 ; i < speed.length ; i ++){
list.add(new Staff(speed[i] , efficiency[i]));
}
// 2. 先通过员工的效率进行降序
Collections.sort(list , (Staff staff1, Staff staff2) -> staff2.e - staff1.e );
// 3. 按照员工的速度进行升序, 维护一个大小为 k 的优先队列
PriorityQueue<Staff> queue = new PriorityQueue<>( (staff1 , staff2) -> staff1.s - staff2.s);
long ans = 0 , sum = 0; // ans 最终的结果 , sum 维护 k-1 个数的和
for(Staff temp_staff : list){
// 因为 list 中是按照员工的效率降序的
// 那么当前的员工就是第k个员工且是最小效率的
long minE = temp_staff.e;
long sumS = sum + temp_staff.s; // sumS 是 k 个的和
ans = Math.max(ans , minE * sumS);
sum += temp_staff.s; // 这里的 sum 是滑动窗口中 k 名员工的速度和
queue.offer(temp_staff);
if(queue.size() == k){ // 移除当前窗口中 速度最小的员工
sum -= queue.poll().s;
}
}
return (int) ( ans % MOD );
}
}