目录
出题方式
挖空出题即是找到一个
终盘(答案盘)
,在终盘上按照规则挖空形成
初盘
,挖空法的优点是:由于提前找到了答案盘,无论按何规则挖空,所得初盘一定有解。
用挖空法完整的出一道数独题只需要两个步骤:
- 按照数独游戏规则随机生成终盘
- 按照一定的挖空规则尽量生成只有唯一解的初盘
本文章内容仅叙述强制生成终盘的实现过程。
强制生成
强制生成即在数独盘上9×9个格子上依次随机填数,同时符合数独规则。
由于每个格子的填入都是随机的,终盘生成过程中会出现死盘,即无解的情况。出现无解时可以回溯(即倒退),但为了简化代码,也可以选择直接再次重新生成。
流程思路
- 按照宫从左到右、从上到下的顺序进行随机填数,每个格子填数时判断行和列是否有重复的数字
- 设置一个宫的不重复随机数,因为以宫为单位填数,每次填入一个数后,便在该宫的候选数中去掉该数,每个宫重置候选数
- 设置一个格子的不重复随机数,其初始候选数为该格子所在宫的候选数,当尝试填入一个数字后检测到行或列有重复时,在候选数中去掉该重复的数,并再次生成一个随机数尝试填入
- 由于按照宫的顺序填数,每次进行行列检测时只需检测该位置前的数(左与上)
- 实体化数独盘对象时,在构造方法中直接完成终盘的填数,实体化后直接使用
声明与初始化
总览
新建类的构成如下:
//强制生成终盘的类
public class Force {
//成员变量
public int base[][]; //数独盘矩阵
public boolean isSuccess; //矩阵是否有解
private int IND[]; //默认数字
private int Ind[]; //宫内可取数字
private int ind[]; //格内可取数字
//构造方法
public Force(); //初始化、填充随机数
//成员方法
private void setBese(); //尝试填入一个数字
private static int getRow(); //宫内编号转化行数
private static int getCol(); //宫内编号转化列数
private int toRand(); //生成范围内随机数
private int[] shrinkage(); //数组缩容
}
新建一个类作为一个终盘
代码如下:
package SudokuCreate;
//强制生成终盘:按宫生成,按行列检测
public class Force {
public int base[][];//面板矩阵
public boolean isSuccess;//矩阵是否有解
private int IND[];//默认数字
private int Ind[];//宫内可取数字
private int ind[];//格内可取数字
}这个强制生成终盘的类在数独创建的包目录下。
这个类拥有以下成员变量:
-
二维整型数组
base
:作为终盘的面板,记录终盘上每个格子上的数字 -
逻辑变量
isSuccess
:表征终盘的生成是否成功,即是否出现了死盘的情况 -
向量
IND
:默认的候选数字,即1~9 -
向量
Ind
:每个宫内的候选数字 -
向量
ind
:每个格子的候选数字
其中,
base
和
isSuccess
是公开的,其他对象可以直接访问,三个候选数字向量是私有的,只在本类中向终盘填数时使用。
在构造方法中对变量初始化
代码如下:
//构造方法
public Force() {
//初始化
this.base = new int[9][9];
this.isSuccess = false;
this.IND = new int[] {1,2,3,4,5,6,7,8,9};
Ind = Arrays.copyOf(IND, IND.length);
ind = Arrays.copyOf(Ind,Ind.length);
}整型数组的默认初值是0。数组直接相等会使前者指向后者,两者共用内存,一起改变,这显然不是我们需要的,故用copyOf()方法进行复制。需要引用:
import java.util.Arrays;
在构造方法中对遍历数独盘
在构造函数中直接实现向盘内填数,在其他类中调用时,将本类实体化时后即可访问已完成的终盘数据
base
。代码如下:
//构造方法
public Force() {
/*初始化部分*/
//填充随机数
//i:宫编号 j:宫内格编号
for(int i=1;i<=9;i++) {
//每个新的宫开始时重置宫候选为默认候选
Ind = Arrays.copyOf(IND, IND.length);
for(int j=1;j<=9;j++) {
//每个格子的初始候选为所在宫此时的候选
ind = Arrays.copyOf(Ind,Ind.length);
/*对每个格子填数*/
}
}
}用i遍历每个宫,用j遍历宫内每个格子。宫相对于盘、格相对于宫的顺序都是从左到右、从上到下。
每个宫填数前,宫候选
Ind
重置为默认候选
IND
;每个格子开始填数前,格候选重置为当前宫候选。
准备工作结束,接下来需要实现随机数的生成与不重复、行列的重复检测、向格子内填数。
填数
不重复随机数的生成
避免生成重复的随机数可以大幅减少运算量,缩短运行时间。
生成不重复随机数的思路是:
生成一个随机索引值,供候选数组引用,每次引用后在该候选数组中删除引用的元素。
生成随机数代码:
//生成范围内随机数
private int toRand() {
int n = ind.length;
int r = (int)(Math.random()*n);
return r;
}获取格子候选数的个数n,Math.random()方法随机生成0~1的双精度浮点数,将其乘以n再强制转化为整型(向下取整)后,得到范围再0~n区间内的随机整数。以该数作为格候选数ind的索引,就可得到一个可以尝试填入格子里的数字。
每当一个数正式填入后,要在宫候选数组中去掉这个数;每当一个数尝试填入失败后(行类重复),要在格候选数组中去掉这个数。在数组中删除指定元素的代码如下:
//数组缩容
private int[] shrinkage(int[] arr,int r) {
arr[r] = arr[arr.length-1];
arr = Arrays.copyOf(arr,arr.length-1);
return arr;
}arr为需要删除元素的数组,r为需要删除元素在数组中的索引。
其原理为:
将数组最后一位元素赋到待删除元素位置上,再将最后一位元素删除
(通过只复制数组的前n-1项实现)。
原理图示(GIF):
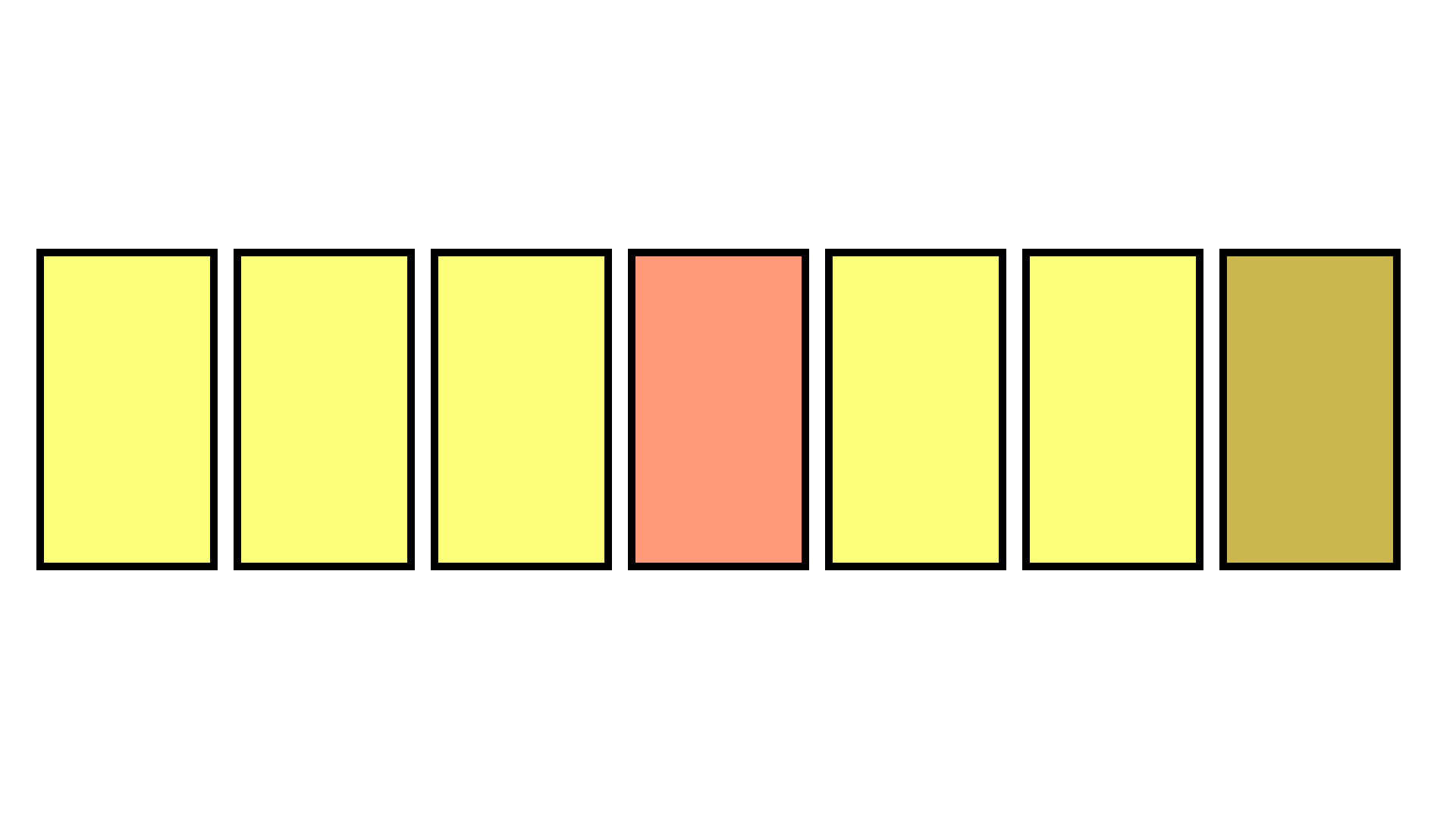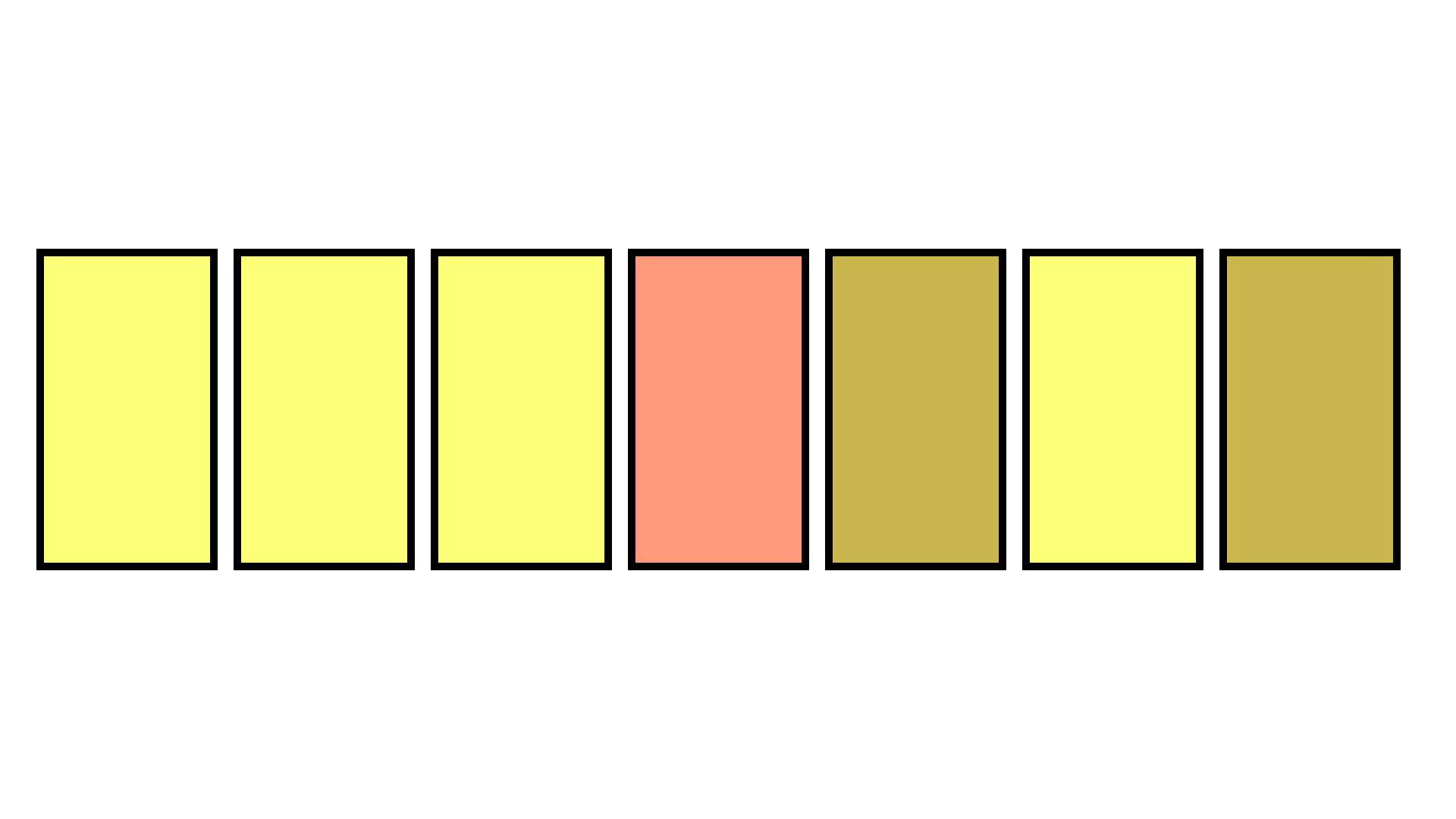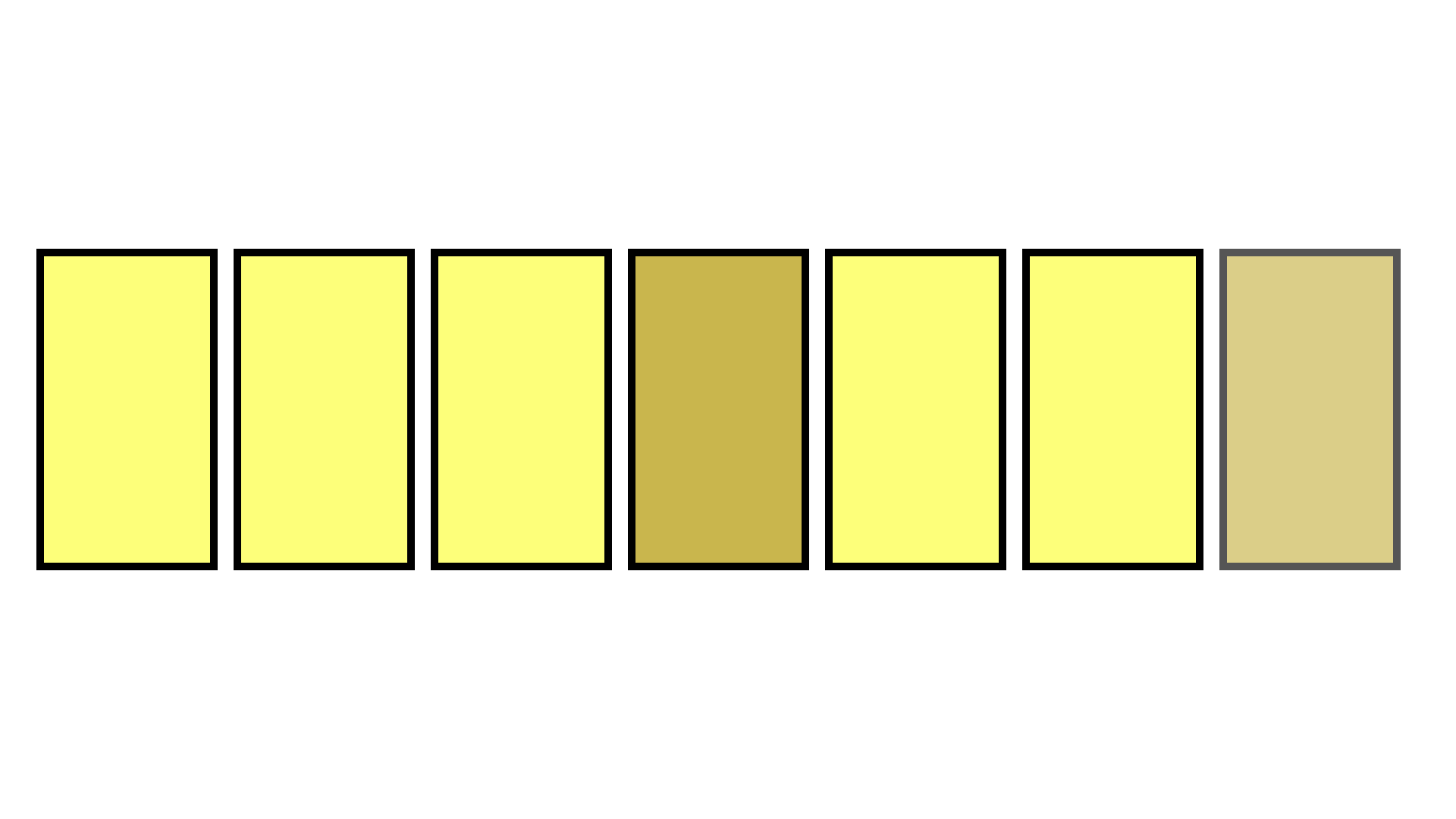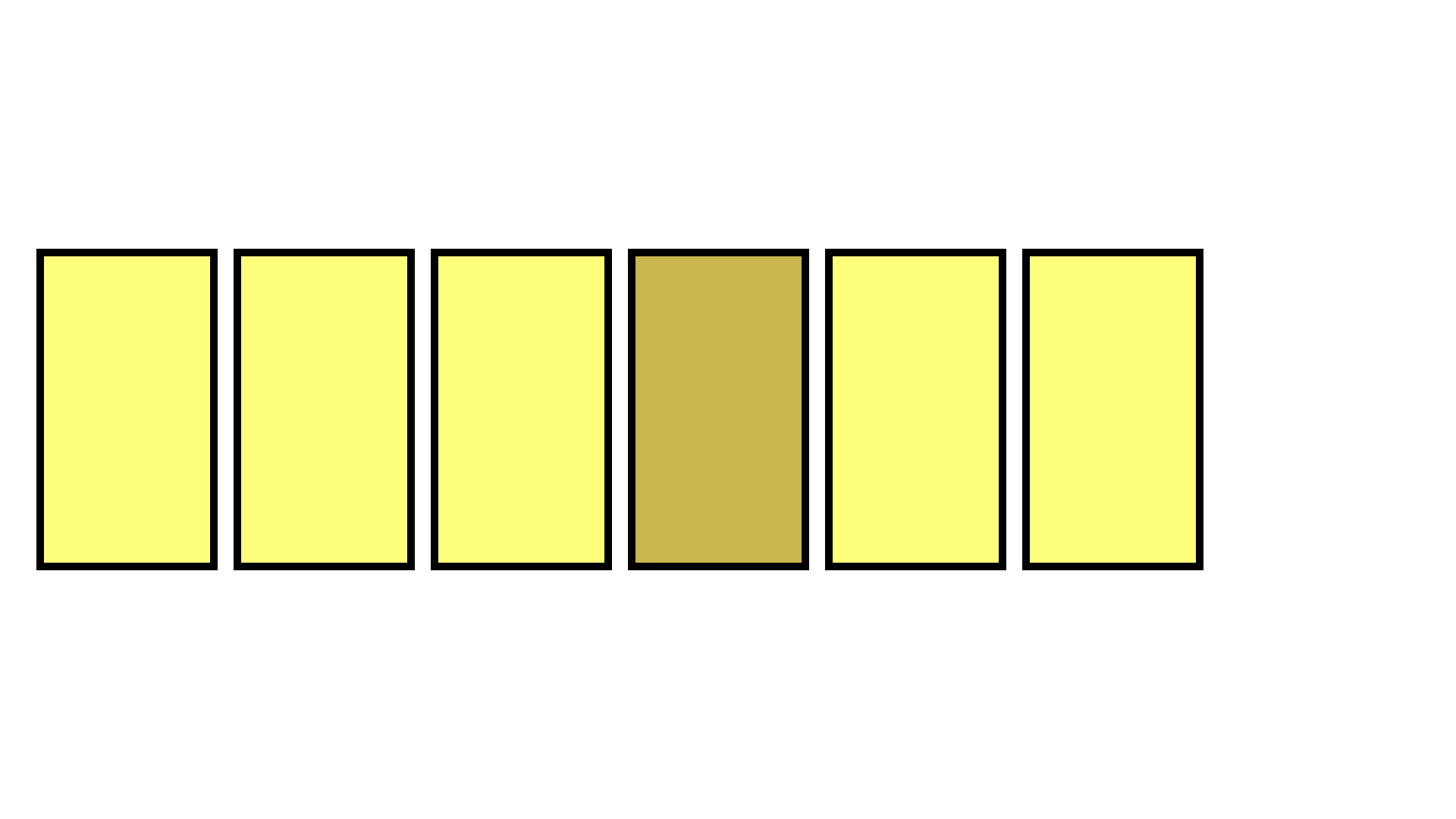
如此删除元素后,一般数组中元素顺序会发生改变,但由于每次调用数组时都是提供一个随机索引,故而顺序的改变没有影响。
在一个填充数字的方法中调用以上两个方法:
//填充数字
private void setBese(int i,int j) {
int n = ind.length;
//尝试填入一个数字
for(int k=1;k<=n;k++) {
int r = toRand();
int rand = ind[r];
/*行独立检测代码*/
/*列独立检测代码*/
/*若重复,格内可取数字减一。跳过后面代码,取下一个数继续循环*/
/*若未重复,填入数字,宫内可取数字减一。自己结束循环*/
}
}
获取尝试前
ind
的长度,作为尝试的总次数,因为
ind
会随着尝试而缩短,需要提前读取长度量。
获取随机索引,代入
ind
获得用以尝试填入的数字,进行行列的重复检验。
行列重复检验
在构造函数中,按宫顺序遍历数独盘上元素,需要将宫序号i与宫内格子序号j转化为数独盘上的行和列坐标。坐标的转换类似进制的转换。
列坐标中:
- 宫1、4、7内格子的列数为 0×3(+1、+2、+3)
- 宫2、5、8内格子的列数为 1×3(+1、+2、+3)
- 宫3、6、9内格子的列数为 2×3(+1、+2、+3)
即需要函数关系使得:
- f(1)=f(4)=f(7)=0
- f(2)=f(5)=f(8)=1
- f(3)=f(6)=f(9)=2
这是一个以3为周期的函数,依次递增的周期函数通过
除法取余数
实现。格序号j的转化和宫序号i的转化相似。
设置一个方法,实现转化的对应函数:
//宫内编号转化列数
private int getCol(int i,int j) {
int col;
col = (i-1)%3*3+(j-1)%3+1;
return col;
}行坐标与列坐标类似
- 宫1、2、3内格子的行数为 0×3(+1、+2、+3)
- 宫4、5、6内格子的行数为 1×3(+1、+2、+3)
- 宫7、8、9内格子的行数为 2×3(+1、+2、+3)
即需要函数关系使得:
- f(1)=f(2)=f(3)=0
- f(4)=f(5)=f(6)=1
- f(7)=f(8)=f(9)=2
这是一个以3为跨度,依跨度递增的函数,通过
除法取商数
实现。格序号j的转化和宫序号i的转化相似。
设置一个方法,实现转化的对应函数:
//宫内编号转化行数
private int getRow(int i,int j) {
int row;
row = (i-1)/3*3+(j+2)/3;
return row;
}为了便于理解与验算,以上两个方法返回的数值分别为格子所在的列数和行数,作为数组索引时需要减去一。
在填充数字方法
setBese()
中,进行行列重复检测:
//填充数字
private void setBese(int i,int j) {
/*获取尝试次数n*/
int row = getRow(i,j);
int col = getCol(i,j);
//尝试填入一个数字
for(int k=1;k<=n;k++) {
/*获取随机数部分*/
boolean isRepeat = false;//表示该次尝试是否出现重复
//行独立检测
for(int x=0;x<col-1;x++) {
if(base[x][row-1]==rand) {isRepeat = true;break;}
}
//列独立检测
for(int y=0;y<row-1;y++) {
if(base[col-1][y]==rand) {isRepeat = true;break;}
}
/*重复或不重复进行对应操作*/
}
}获取格子所在的行数和列数。在每次尝试中生成随机数后,依次向前(行向左、列向上)进行比较(后面的格子还未填数无需向后比较)。若出现重复,将isRepeat 设置为true并且跳出比较循环,执行后续操作;若比较遍历完成后均无重复,则isRepeat不进行更改,默认值为false,按顺序执行后续操作。
进行填数
完成重复检测后,根据检测结果执行填数操作:
//填充数字
private void setBese(int i,int j) {
isSuccess = false;
//尝试填入一个数字
for(int k=1;k<=n;k++) {
/*随机数部分*/
/*独立检验部分*/
//重复,格内可取数字减一,跳过取下一个数
if(isRepeat) {
ind = shrinkage(ind,r);
continue;
}
//若未重复,填入数字,宫内可取数字减一
isSuccess = true;
base[col-1][row-1] = rand;
int p = 0;
for(int m=0;m<Ind.length;m++) {
if(Ind[m]==rand) {p=m;break;}
}
Ind = shrinkage(Ind,p);
break;
}
}
每个格子的尝试开始前,将
isSuccess
(判断死盘)默认设置为false。开始逐次尝试。
-
若该次尝试出现重复,调用数组缩容方法
shrinkage()
将
格候选数
ind
字减一,跳过后续代码,取下一个数再次进行尝试 -
若该次尝试无重复,即可填入盘中,同时设置
isSuccess
为true,表示进度到达此格时仍有解。
将
宫候选数
Ind
字减一。结束尝试。
由于尝试中
ind
不断变化,会与
Ind
有所差异,需要先找到填入数字在
Ind
中的索引方可调用
shrinkage()
。
为减少程序运算量,可在行检测后添加一段出现重复操作的代码:
//尝试填入一个数字
for(int k=1;k<=n;k++) {
/*.................*/
/*行独立检测*/
//重复,格内可取数字减一,跳过取下一个数
if(isRepeat) {
ind = shrinkage(ind,r);
continue;
}
/*列独立检测*/
//重复,格内可取数字减一,跳过取下一个数
if(isRepeat) {
ind = shrinkage(ind,r);
continue;
}
/*若未重复...........*/
}当行检测出重复时,直接进行下一次尝试,无需再进行列检测。
若每次尝试均失败,填入代码部分始终被跳过,
isSuccess
默认为false;若尝试成功一次,
isSuccess
设置为true。无论结果如何,该格子的填数结束,
setBese()
调用结束。
重复与死盘
一次填入结束后,根据结果进行判断:
- 若填入成功,进行下一个格子的填入
- 若填入失败,该盘无解,结束填入
回到构造方法:
//构造方法
public Force() {
/*初始化部分*/
//填充随机数,按宫遍历格子
for(int i=1;i<=9;i++) {
/*重置Ind*/
for(int j=1;j<=9;j++) {
/*重置ind*/
setBese(i,j);
if(!isSuccess) {return;}
}
}
}若一次填入后出现无解情况,结束构造函数,否则循环继续。
自此,强制生成终盘的类定义完成。
完整代码
最终完成的代码如下:
package SudokuCreate;
import java.util.Arrays;
//强制生成终盘:按宫生成,按行列检测
public class Force {
public int base[][];//面板矩阵
public boolean isSuccess;//矩阵是否有解
private int IND[];//默认数字
private int Ind[];//宫内可取数字
private int ind[];//格内可取数字
//构造方法
public Force() {
//初始化
this.base = new int[9][9];
this.isSuccess = false;
this.IND = new int[] {1,2,3,4,5,6,7,8,9};
Ind = Arrays.copyOf(IND, IND.length);
ind = Arrays.copyOf(Ind,Ind.length);
//填充随机数
//i:宫编号 j:宫内格编号(先行后列)
for(int i=1;i<=9;i++) {
Ind = Arrays.copyOf(IND, IND.length);
for(int j=1;j<=9;j++) {
ind = Arrays.copyOf(Ind,Ind.length);
setBese(i,j);
if(!isSuccess) {return;}
}
}
}
//填充数字
private void setBese(int i,int j) {
int row = getRow(i,j);
int col = getCol(i,j);
isSuccess = false;
int n = ind.length;
//尝试填入一个数字
for(int k=1;k<=n;k++) {
boolean isRepeat = false;
int r = toRand();
int rand = ind[r];
//行独立检测
for(int x=0;x<col-1;x++) {
if(base[x][row-1]==rand) {isRepeat = true;break;}
}
//重复,格内可取数字减一,跳过取下一个数
if(isRepeat) {
ind = shrinkage(ind,r);
continue;
}
//列独立检测
for(int y=0;y<row-1;y++) {
if(base[col-1][y]==rand) {isRepeat = true;break;}
}
//重复,格内可取数字减一,跳过取下一个数
if(isRepeat) {
ind = shrinkage(ind,r);
continue;
}
//若未重复,填入数字
isSuccess = true;
base[col-1][row-1] = rand;
//宫内可取数字减一
int p = 0;
for(int m=0;m<Ind.length;m++) {
if(Ind[m]==rand) {p=m;break;}
}
Ind = shrinkage(Ind,p);
break;
}
}
//宫内编号转化行数
private int getRow(int i,int j) {
int row;
row = (i-1)/3*3+(j+2)/3;
return row;
}
//宫内编号转化列数
private int getCol(int i,int j) {
int col;
col = (i-1)%3*3+(j-1)%3+1;
return col;
}
//生成范围内随机数
private int toRand() {
int n = ind.length;
int r = (int)(Math.random()*n);
return r;
}
//数组缩容
private int[] shrinkage(int[] arr,int r) {
arr[r] = arr[arr.length-1];
arr = Arrays.copyOf(arr,arr.length-1);
return arr;
}
}
测试分析
在其他程序中将其对象实体化后需要访问
isSuccess
,不断重复创建对象直到成功生成一个完整的终盘。由于一但出现死盘便直接结束构造函数,成功生成的效率很低,经测试:
package test;
import SudokuCreate.Force;
import java.io.*;
public class test {
public static void main(String[] args){
int sum = 0;
int N = 10000;
for(int m=0;m<N;m++) {
Force testF = new Force();
if(testF.isSuccess) {sum++;}
testF = null;
}
System.out.println(sum);
}
}每创建一万个对象,成功个数在25~40之间。虽然成功率低,但创建一万个对象所用时间小于1s,足以满足使用需求。
若要提高单次成功率,可采用回溯的方法,即不断倒回上一个节点重新生成,直到成功。