博客

实际采集的近红外光谱数据成分复杂，除了基本的特征变量之外，还有背景基线、噪声等信号，通过分析实际近红外光谱分析技术发现，检测对象近红外光谱数据的主要成分来源于采集环境和设备所导致的基线，或者是所谓的背景，所以在分析建模之前，只有将背景基线从高维的、非零变量的复杂数据中滤除，才能从获得纯光谱数据中选择出分析对象对应的特征数据，目前使用最广的基线校正方法是由中南大学化工学院梁逸曾教授和张志敏老师于2010年提出的迭代自适应加权惩罚最小二乘法（adaptive iteratively reweighted penalized least squares, airPLS）.

目前针对基线校正很多，但是应用最广、效果最好的还是airPLS，除此之外，很多改进方法存在很大缺陷，例如扩展性差等问题，此处只介绍airPLS。关于惩罚最小二乘在另外一篇文章中会介绍，在airPLS方法中，采用了基于误差的迭代加权策略，每一个点的权重更新基于上一次循环拟合的基线和原始信号之间的差异，具体表达如下：

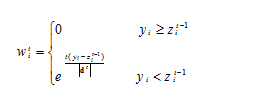
其中t表示第t次迭代，y表示原始信号，z表示拟合基线，

表示

中小于变量的绝对值之和。如式所示，在特征区域，airPLS迭代的权重为0，而对于非特征区域，即基线区域，其权重系数的更新均基于迭代过程中的误差。具体MATLAB代码如下所示：

function [Xc,Z]= airPLS(X,lambda,order,wep,p,itermax)
[m,n]=size(X);
wi = [1:ceil(n*wep) floor(n-n*wep):n];
D = diff(speye(n), order); DD = lambda*D'*D;
for i=1:m
    w=ones(n,1);
    x=X(i,:);
    for j=1:itermax
        W=spdiags(w, 0, n, n);
        C = chol(W + DD);
        z = (C\(C'\(w .* x')))';
        d = x-z;
        dssn= abs(sum(d(d<0)));
        if(dssn<0.001*sum(abs(x))) 
            break;
        end
        w(d>=0) = 0; w(wi)   = p;
        w(d<0)  = j*exp(abs(d(d<0))/dssn);
    end
    Z(i,:)=z;
end
Xc=X-Z;

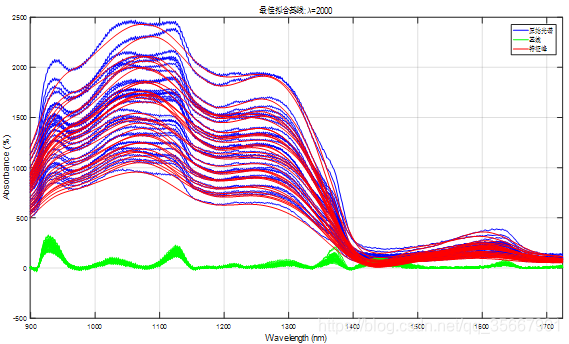
最后贴一张自己利用airPLS做的基线校正结果：

个人新建立的weixin公众号，光谱学与光谱分析，欢迎大家关注