概念
树是一种重要的非线性数据结构,直观地看,它是数据元素(在树中称为结点)按分支关系组织起来的结构,很象自然界中的树那样。 树是由结点或顶点和边组成的(可能是非线性的)且不存在着任何环的一种数据结构。没有结点的树称为空(null或empty)树。一棵非空的树包括一个根结点,还(很可能)有多个附加结点,所有结点构成一个多级分层结构
结点:下面就是一个简单的树, 每一个元素都称为一个结点,而最顶端的是根结点,最末端的是叶子结点, 每个结点有零个或多个子结点;每一个非根结点有且只有一个父结点;除了根结点外,每个子结点可以分为多个不相交的子树
度:度就是一棵树里面最大的宽度,下图树(包含子树)的子结点数最大都不超过2所以该树的度为2
深度: 由根结点到叶子结点组成该树各结点的最大层次
二叉树
二叉树又分为二叉查找树、完全二叉树、满二叉树、平衡二叉树、红黑树、B树
为什么二叉树也还要区分那么多种类型?因为单种二叉树不能完全保证我们运行或储存效率,所以需要多种类型二叉树应对不同的使用场景
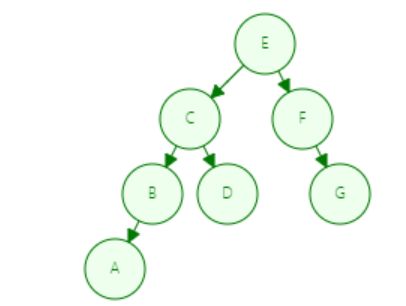
下面先看一下二叉查找树
录入的顺序 为 E–>F–>C–>B–>D–>A–G
二叉树与树的区别
1.树的度没有限制,二叉树的度最大为2
2.二叉树每个子树都是有序的,例如二叉树的左子树如果非空,左子树所以结点的值都小于根节点的值,如果右子树非空,则右子树所有结点的值都大于根结点的值(左小右大)
因为二叉树左小右大的特点,所以二叉查找树有个比较极端的情况
录入的顺序 为 A–>B–>C–>D–>E
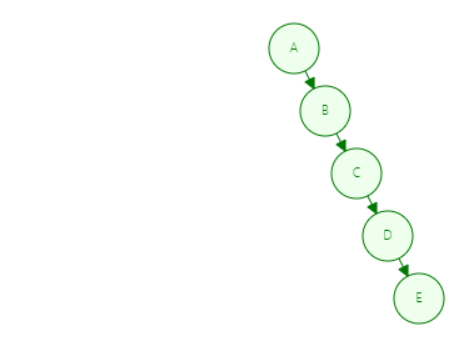
从小到大的开始录入,大的永远在右边,就造成了右斜树,与链表(线性结构)一样这种树并不能保证我们的运行效率
平衡二叉树(AVL树)
平衡二叉树是基于二叉查找树优化而来的
录入顺序: A–>B–>C–>D–>E–>F
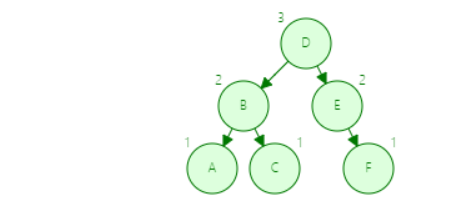
录入顺序与一般二叉树一样,都是从小到大开始录入,但是平衡二叉树每次插入数据会判断数据的大小,从而进行左右旋转,使得我们的数据分布均匀,保证了一定的运行效率
平衡二叉树与二叉查找树的区别主要体现在二叉查找树的根结点不能变,平衡二叉树为了保证根结点左右子树的层级差不超过1,所以会进行左右旋转操作,这个时候根结点就会发生改变
优点:因为左右子树结点数量相差较少,所以查询速度极快
缺点:插入数据时候因为旋转次数不确定,所以插速度会相对慢
红黑树
性质:
1. 节点是红色或黑色。
2. 根节点是黑色。
3 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
4. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
红黑树与平衡二叉树相似,平衡二叉树基于 根结点左右子树的层级差不超过1 进行旋转操作,而红黑树则是基于 没有任何一条路径比其他路径长两倍以上进行(旋转次数不超过3次,新增不超过2次,删除不超过3次)旋转
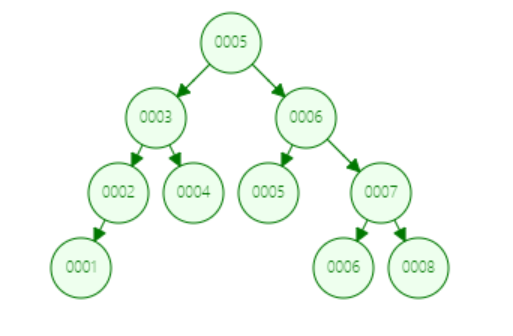
录入顺序: A–>B–>C–>D–>E–>F–>G
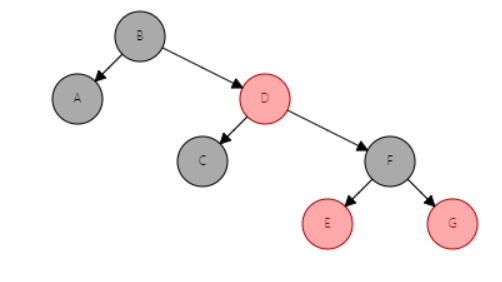
录入顺序: A–>B–>C–>D–>E–>F–>G–>H
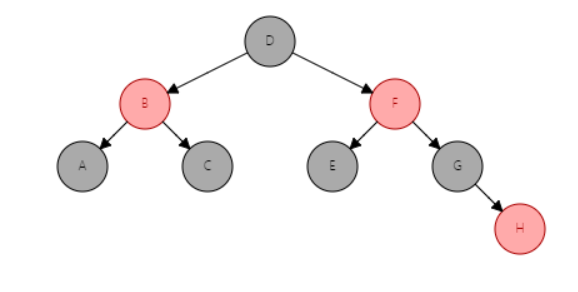
由第一张红黑树图可以看出,红黑树的平衡度并没有AVL树平衡度那么严格(只保持黑结点平衡)由于旋转次数是保证在3以内的,所以插入或删除结点时候性能要比平衡二叉树好
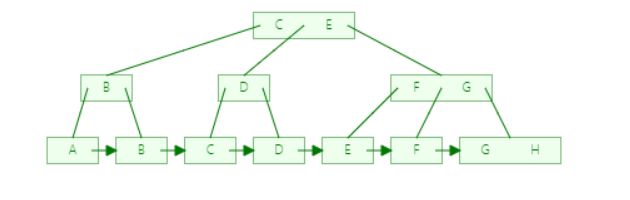
B树 — Balance-tree(平衡多路查找树)
下面是一棵三阶的B树
录入顺序: A–>B–>C–>D–>E–>F–>G–>H
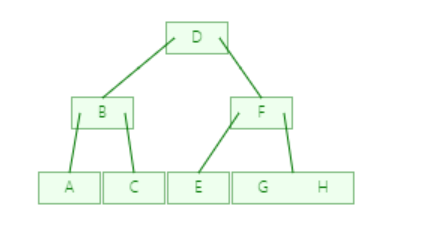
阶:每个B树都有个指定的阶(M),阶决定了每个结点最多拥有多少个子结点,例如三阶B树每个结点最多只能拥有三个子结点
阶与度不一样,上图树的度为2,阶为3,但是阶决定度的最大值
关键字:例如每一个结点里面的值就是一个关键字,例如

,该结点就有2个关键字,G和H
B树的性质
1.每个结点里面的关键字数量最多为M-1,根节点最少可以只有1个关键字,非根节点至少有M/2(上取整)个关键字。
2.每个结点至少有2个子结点,叶子结点除外
3.除根结点以外的所有结点(不包括叶子结点)的度数正好是关键字总数加1
4.B树的叶子结点都是在同一层
例如现在要录入一个A-E的三阶B树
先录入A和B

接下来要录入C,因为根结点的关键字数量为1到M-1和每个结点至少有2个子结点,所以录入C的时候应该B作为根结点,A和C作为子结点
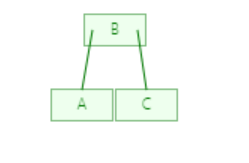
插入D
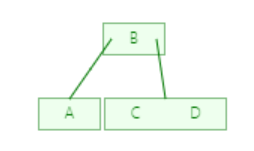
插入E
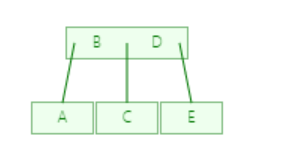
插入元素时,如果树结构不满足B树的性质时,就会进行合并或分裂
B树与二叉树的比较
下面使用元素相同的平衡二叉树(二叉树里面查询快)与B树的查询作比较
平衡二叉树查询 H
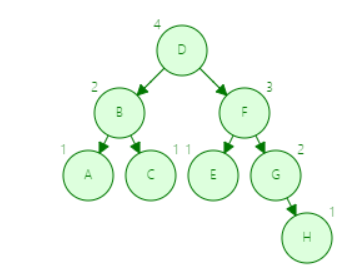
第一步
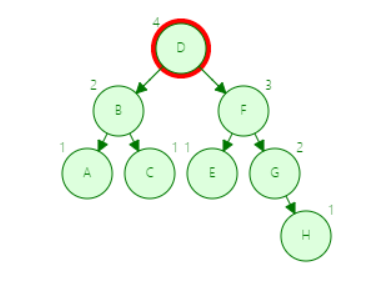
第二步
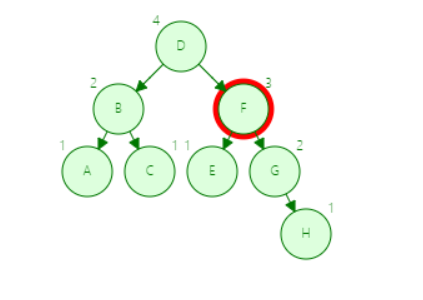
第三步
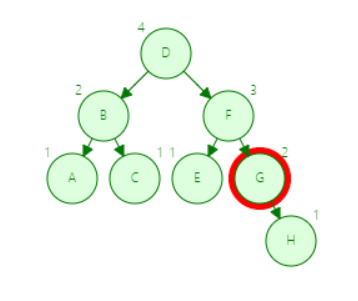
第四步
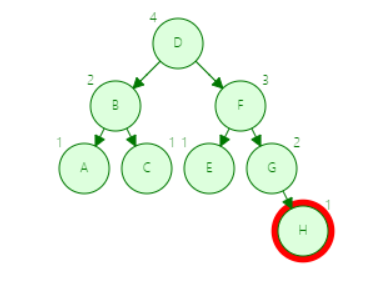
B树查询 H

第一步
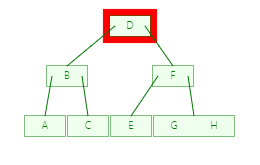
第二步
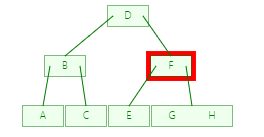
第三步
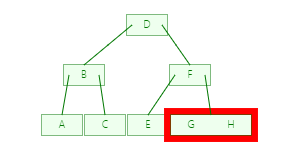
第四步
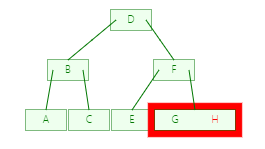
虽然看上去都是需要四步才能完成H的查询,因为树结构是非线性的,每个结点的地址是不连续的,所以B树的第四步是在一块内存内比较,要比平衡二叉树的第四步重新寻找地址快很多,并且,如果数据是存放在磁盘而不是内存的时候,每次IO操作性能消耗非常大,且随着数据量增大,两者的性能差距更加明显
B+树
B+树与B树的区别在于B+树每一个元素都存在于叶子结点,非叶子结点仅仅提供索引操作,必须到叶子结点才会命中
这样保证了我们寻找任意一个元素时,所需要的时间都是一样的
并且叶子结点以链表形式连接,这样有利于遍历所有数据时候,只需要进行线性查询,而不用一层一层遍历