1、迭代
迭代是重复反馈过程的活动,其目的通常是为了逼近所需目标或结果。每一次对过程的重复称为一次“迭代”,而每一次迭代得到的结果会作为下一次迭代的初始值。
目前对于c语言来说,迭代可以简单认为是循环结构。

递归效率低下,循环验证麻烦。
迭代可以转换为递归,但递归不一定能转换为迭代。
转换方法:
将递归算法转换为非递归算法有两种方法,一种是直接求值(迭代),不需要回溯;另一种是不能直接求值,需要回溯。前者使用一些变量保存中间结果,称为直接转换法,后者使用栈保存中间结果,称为间接转换法。
直接转换法
直接转换法通常用来消除尾递归(tail recursion)和单向递归,将递归结构用迭代结构来替代。(单向递归 → 尾递归 → 迭代)
间接转换法
递归实际上利用了系统堆栈实现自身调用,我们通过使用栈保存中间结果模拟递归过程,将其转为非递归形式。
尾递归函数递归调用返回时正好是函数的结尾,因此递归调用时就不需要保留当前栈帧,可以直接将当前栈帧覆盖掉。
例:求n的阶乘
采用循环的方式
//采用循环方式
int Facl(int n)
{
int i = 0;
int ret = 1;
for (i = 1; i <= n; i++)
{
ret = ret* i;
}
return ret;
}
int main()
{
int n = 0;
int ret = 0;
scanf("%d", &n);
ret = Facl(n);
printf("%d\n", ret);
return 0;
}结果
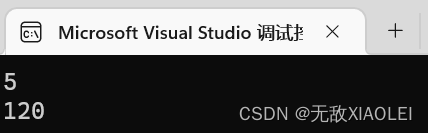
采用递归的方式
//采用递归方式
int Fac2(int n)
{
if (n < 1)
return 1;
else
return n * Fac2(n - 1);
}
int main()
{
int n = 0;
int ret = 0;
scanf("%d", &n);
ret = Fac2(n);
printf("%d\n", ret);
return 0;
}结果:

求第N个斐波那契数:
//斐波那契数列
int Fib(int n)
{
if (n <= 2)
return 1;
else
return Fib(n - 1) + Fib(n - 2);
}
int main()
{
int n = 0;
int ret = 0;
scanf("%d", &n);
ret = Fib(n);
printf("ret = %d\n", ret);
return 0;
}

有兴趣的可以算50以上的。。。。。
测试第三个斐波那锲数的计算次数
int count = 0;
int Fib(int n)
{
if(n==3)
{
count++;
}
if (n <= 2)
return 1;
else
return Fib(n - 1) + Fib(n - 2);
}
int main()
{
int n = 0;
int ret = 0;
scanf("%d", &n);
ret = Fib(n);
printf("ret = %d\n", ret);
printf("count = %d\n", count);
return 0;
}结果

采用循环方式计算
//采用循环方式计算
int Fib(int n)
{
int a = 1;
int b = 1;
int c = 1;
while (n > 2)
{
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
int main()
{
int n = 0;
int ret = 0;
scanf("%d", &n);
ret = Fib(n);
printf("ret = %d\n", ret);
/*printf("count = %d\n", count);*/
return 0;
结果

2、一维数组的创建和初始化
2.1数组的创建
数组是一组相同类型元素的集合。
数组的创建方式:
type_t arr_name [const_n];
// type_t 是指数组的元素类型
// const_n 是一个常量表达式,用来指定数组的大小
例:
int main()
{
//创建一个数组存放整型10个
int arr[10];
char arr2[5];
return 0;
}
注:[]中要给一个常量,不能是变量
2.2数组初始化
数组的初始化是指,在创建数组的同时给数组的内容一些合理初始值(初始化)。
例:
int arr1[10] = {1,2,3};//不完全初始化,剩余元素默认为0
int arr2[] = {1,2,3,4};
int arr3[5] = {1,2,3,4,5};
char arr4[3] = {'a',98, 'c'};
char arr5[] = {'a','b','c'};
char arr6[] = "abcdef";
注:数组在创建的时候如果想不指定数组的确定的大小就得初始化。数组的元素个数
根据初始化的内容来确定
。
例:
int main()
{
char arr[] = "abcdef";
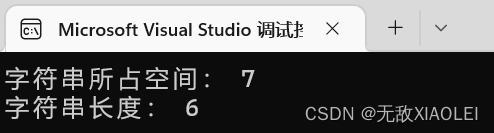
printf("字符串所占空间: %d\n", sizeof(arr));//sizeof 计算arr所占空间的大小,数组中包含7个元素(含\0),7*1=7
printf("字符串长度: %d\n", strlen(arr));//strlen计算字符串的长度,\0之前的个数,所以是6
return 0;
}结果:
2.3、一维数组的使用
操作符:
[ ] ,下标引用操作符
。它其实就数组访问的操作符。
例
int main()
{
char arr[] = "abcdef";
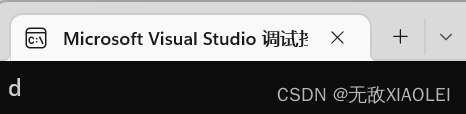
printf("%c\n", arr[3]);
return 0;
}结果
例
int main()
{
int arr[] = { 1,2,3,4,5,6,7,8,9,0 };
int sz = sizeof(arr) / sizeof(arr[0]);//总大小除元素大小=个数
int i = 0;
for (i = 0; i < sz; i++)
{
printf("%d ", arr[i]);
}
return 0;
}结果

总结:
1. 数组是使用下标来访问的,下标是从0开始。
2. 数组的大小可以通过计算得到。
2.4一维数组在内存中的存储
//数组在内存中的储存
int main()
{
int arr[] = { 1,2,3,4,5,6,7,8,9,0 };
int sz = sizeof(arr) / sizeof(arr[0]);//总大小除元素大小=个数
int i = 0;
for (i = 0; i < sz; i++)
{
printf("&arr[%d] = %p\n", i, &arr[i]);
}
return 0;
}结果

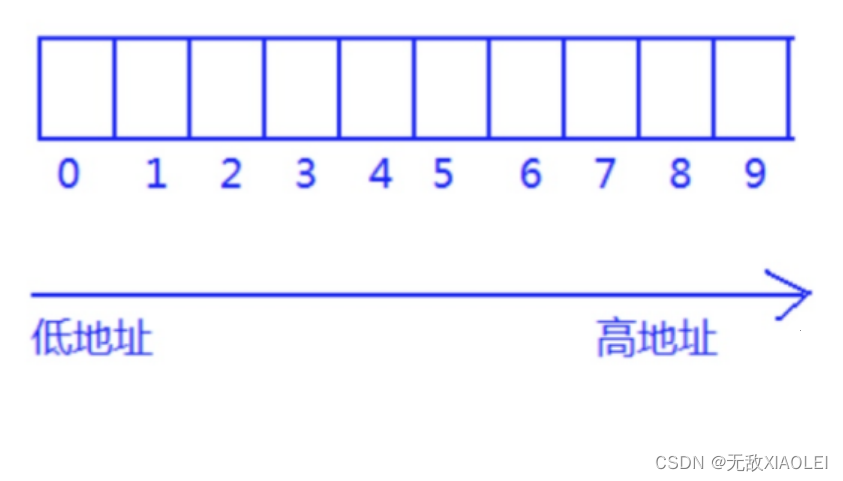
仔细观察输出的结果,我们知道,随着数组下标的增长,元素的地址,也在有规律的递增。 由此可以得出结论:数组在内存中是连续存放的。
3、二维数组的创建和初始化
3.1二维数组的创建
//数组创建
int arr [3][4];//三行4列
char arr[3][4];
double arr[2][4];
3.2二维数组的初始化
//数组初始化
int arr[3][4] = {1,2,3,4};
int arr[3][4] = {{1,2},{4,5}};
int arr[][4] = {{2,3},{4,5}};
注:行可以省略,但是列不能省略
3.3二维数组的使用
二维数组的使用也是通过下标的方式。
例:
int main()
{
int arr[3][4] = { {1,2,3},{4,5} };
int i = 0;
for (i = 0; i < 3; i++)
{
int j = 0;
for (j = 0; j < 4; j++)
{
printf("%d ", arr[i][j]);
}
printf("\n");
}
return 0;
}结果

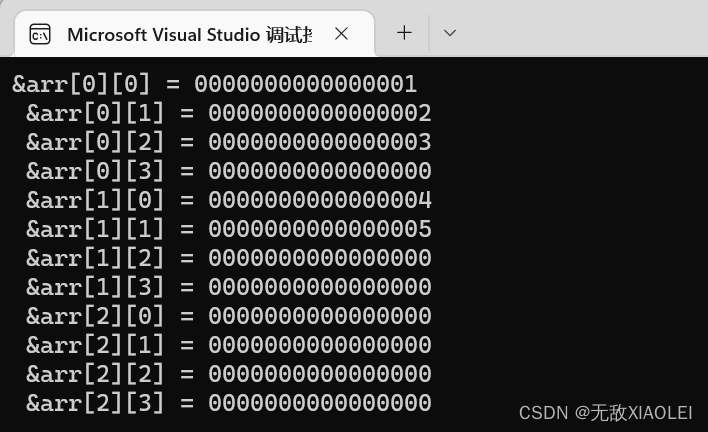
3.4二维数组的存储
二维数组在内存中的存储:其实二维数组在内存中也是连续存储的。
int main()
{
int arr[3][4] = { {1,2,3},{4,5} };
int i = 0;
for (i = 0; i < 3; i++)
{
int j = 0;
for (j = 0; j < 4; j++)
{
printf("&arr[%d][%d] = %p\n ", i, j, arr[i][j]);
}
}
return 0;
}结果