博客

题目描述

题目链接



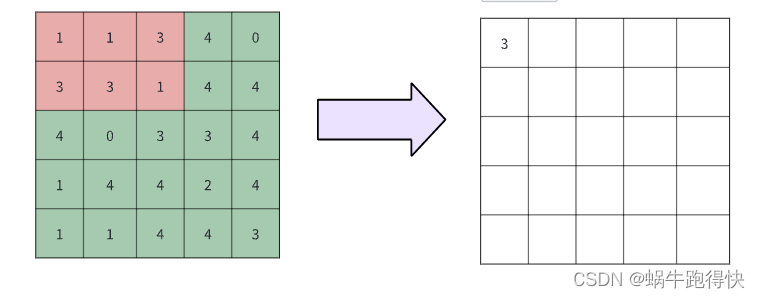
m*n

的窗口在

M*N

的二维数组中滑动，以左上角为原点，进行窗口滑动，边缘以临近行进行补齐(repeat)，滑动步伐

k=1

，得到每次滑动的最大值，将滑动窗口输出值做直方图统计且排序，分别输出

直方图

的X和Y值。

输入描述：

m(行)*n(列)的滑动窗口(m<=5, n<=5)
M(行)*N(列)的原始矩阵(M<=1000, N<=1000)，矩阵中值小于256。滑动步伐k=1。

输入顺序描述：

M N m n 
M*N矩阵

输出描述：

Y:直方图统计纵坐标
排序输出X:直方图统计横坐标	
基于X（从小到大）顺序打印输出X和Y值

样例输入：

5 5 2 3
1 1 3 4 0
3 3 1 4 4
4 0 3 3 4
1 4 4 2 4
1 1 4 4 3

样例输出：

2 23
3 4

思路：

参考

LeetCode.239

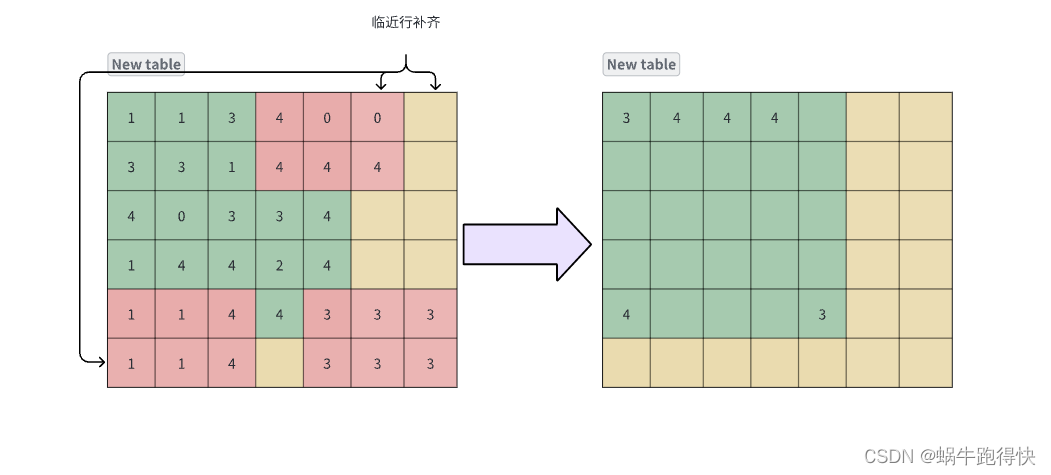
滑动窗口找最大值，按行列分别遍历求滑动窗口最大值，先按行找滑动窗口大小为n的最大值，并将原数组覆盖（新开一个大小相同的也行）；然后按列找滑动窗口最大值，覆盖原数组；遍历完毕后的数组就是所求的结果数组，最后统计结果就OK了。注意的是最后n – 1列和最后m – 1行是特例，相当于求最后几个元素的最大值。

代码

#include <bits/stdc++.h>
using namespace std;
//测试输出
void print(vector<vector<int>> &arr){
    for(auto&i:arr){
        for(auto&j:i){
            cout<<j<<"\t";
        }
        cout<<endl;
    }
}
void find2DMax(vector<vector<int>> &arr,int m,int n){
    int M = arr.size();
    int N = arr[0].size();
    priority_queue<pair<int,int>>pq;
    //每一行滑动窗口最大值
    for (auto &i : arr)
    {
        while(!pq.empty())pq.pop();
        for(int j = 0; j < n;++j){
            pq.push({i[j],j});
        }
        i[0] = pq.top().first;
        for(int j = n; j < N;++j){
            pq.push({i[j],j});
            while(!pq.empty() && pq.top().second <= j - n)
            {
                pq.pop();
            }
            i[j - n + 1] =pq.top().first; 
        }
        //每行倒数n列赋值,是用最后一行补齐
        for(int j = N - n + 1; j < N;++j){
            i[j] = *max_element(i.begin()+j,i.end());
        }
    }
    unordered_map<int,int> hash;//计数
    //每一列滑动窗口最大值
    for (int i = 0; i < N;++i)
    {
        while(!pq.empty())pq.pop();
        for(int j = 0; j < m;++j){
            pq.push({arr[j][i],j});
        }
        arr[0][i] = pq.top().first;
        hash[arr[0][i]]++;
        for(int j = m; j < M;++j){
            pq.push({arr[j][i],j});
            while(!pq.empty() && pq.top().second <= j - m)
            {
                pq.pop();
            }
            arr[j - m + 1][i] =pq.top().first;
            hash[arr[j - m + 1][i]]++; 
        }
        //每列倒数m行赋值
        //保存最后几个元素方便求最值。
        vector<int>temp;
        for(int j = M - m + 1; j < M;++j){temp.push_back(arr[j][i]);}
        for(int j = M - m + 1; j < M;++j){
            arr[j][i] = *max_element(temp.begin()+j - (M - m + 1),temp.end());
            hash[arr[j][i]]++; 
        }
    }
    vector<pair<int,int>> res;
    for(auto &h:hash){
        res.push_back(h);
    }
    //按X从小到大排序
    sort(res.begin(),res.end(),[](pair<int,int>&a,pair<int,int>&b)->bool{return a.first<b.first;});
    for(auto &r:res){
        cout<<r.second<<"\t";
    }
    cout<<endl;
        for(auto &r:res){
        cout<<r.first<<"\t";
    }
    cout<<endl;
}

int main() {

    
    int m , n,M,N;
    //输入数据行列
    cin>>M>>N>>m>>n;
    vector<vector<int>> arr;
    cin>>m>>n;
    cout<<"请输入数据";
    while(M--){
        vector<int> rol;
        int num = N;
        while(num--){
            int a;
            cin>>a;
            rol.push_back(a);
        }
        arr.push_back(rol);
    }
    find2DMax(arr,m,n);
    return 0;
}

输出结果