最近在学习Python与ML，没有时间，不容易抽个时间写个笔记，如果有不足之处还请见谅。之后会抽时间更正。

理论部分

这一部分可以查看周志华的<<机器学习>>，俗称‘’西瓜书‘’。还有Bishop等。梯度下降有很多方法，Adagrad，Stochastic gradient descent，Adam等，比较简单，可自行学习。

Demo Process

如下是部分数据集

，可以自行生成。直接调用python中的

random

库即可(’‘

import random

’’)。






(为便于索引，我在生成后将其转换为矩阵形式。这个可以自行处理，视具体情况而定)

我最后生成

200笔data

,一笔data有

3个feature

（前三列）。最右边是

real label

（即真实的y值，或者说是target）。为什么会有一列1呢?是因为我们在线性回归中，为了便于符号化数学推导，我们将weights与biases封装成一个vector，与feature做inner product。



而一般形式则如下：

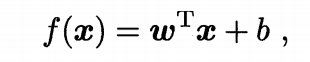
以下是代码实现：

"""导入所需库"""
import random
import sympy
import numpy as np
from matplotlib import pyplot as plt
import math

datas = []

def data_preprocessing(filename):
    """生成数据，这一部分可以自行生成。我这里是按照之前我做过的项目加工了一下而生成的数据"""
    l = []

    with open(filename) as data:
        lines = data.readlines()

    for i in range(len(lines)):
        l.append(lines[i].strip())

    for i in range(len(l)):
        datas.append(l[i].split())

    for i in range(len(datas)):
        for j in range(len(datas[0])):
            datas[i][j] = float(datas[i][j])

    for i in range(len(datas)):
        for j in range(2):
            datas[i].insert(2,random.random())

    for i in range(len(datas)):
        for j in range(len(datas[0])):
            datas[i][j] = round(datas[i][j],4)

def cal_regression_coefficient(xMat,yMat):
    """
    最小二乘法计算回归系数
    :param xMat:  x数据集(矩阵形式)
    :param yMat:  y数据集(矩阵形式)
    :return:      回归系数
    """
    ws = (xMat.T * xMat).I * xMat.T *yMat
    return ws

data_preprocessing('data_linear_regression.txt')

"""处理一下数据,将1放在第四列"""
for i in range(len(datas)):
    del datas[i][0]
    datas[i].insert(3,1)

"""数据转换为矩阵形式,便于处理"""
datas = np.mat(datas)
"""check一下数据集"""
print(datas)
print(type(datas))
print()

"""我们首先做linear Regression.之后再考虑nonlinear Regression"""

"""分离出x数据集和y数据集"""
"""共200个labeled data.训练集--150,测试集--50"""
x_train_datas = datas[:150,:4]
y_train_datas = datas[:150,4]
x_test_datas = datas[150:,:4]
y_test_datas = datas[150:,4]

print(x_train_datas)
print(x_train_datas.shape)
print(y_train_datas)
print(y_train_datas.shape)

"""计算回归系数"""
ws = cal_regression_coefficient(x_train_datas,y_train_datas)
print(ws)
print(type(ws))
print(ws.shape)
"""到此,回归系数计算完毕.最后一个为bias项"""

"""在测试集上计算误差"""
test_error = 0
for i in range(50):
    test_error += (ws.T * x_test_datas[i,:].T) - y_test_datas[i]
print(test_error)


#表示loss funtion损失函数
loss = 0
summation = 0
w1,w2,w3,b = sympy.symbols('w1 w2 w3 b')
w = [w1,w2,w3,b]
for i in range(150):
    loss += (w * x_train_datas[i].T - y_train_datas[i])**2
    # for j in range(4):
    #     summation += w[j]*x_train_datas[i,j]
    # loss += (summation - y_train_datas[i])**2
    # summation = 0
loss = loss.tolist()
loss = loss[0][0]
print(loss)
print(type(loss))
def gradicent_descent():
    """
    梯度下降法计算回归系数(待估参数)
    """
    #随机选取初值
    w_0 = []
    sum_diff_loss_w1 = 0
    sum_diff_loss_w2 = 0
    sum_diff_loss_w3 = 0
    sum_diff_loss_b = 0
    for i in range(4):
        w_0.append(random.gauss(0,10))
    learning_rate = 0.01

    epochs = [0]
    loss_value = [loss.subs({w1:w_0[0],w2:w_0[1],w3:w_0[2],b:w_0[3]})]
    epoch = 0
    print(loss_value)
    while True:
        diff_loss_w1 = sympy.diff(loss,w1).evalf(subs={w1:w_0[0],w2:w_0[1],w3:w_0[2],b:w_0[3]})
        diff_loss_w2 = sympy.diff(loss,w2).evalf(subs={w1:w_0[0],w2:w_0[1],w3:w_0[2],b:w_0[3]})
        diff_loss_w3 = sympy.diff(loss,w3).evalf(subs={w1:w_0[0],w2:w_0[1],w3:w_0[2],b:w_0[3]})
        diff_loss_b = sympy.diff(loss,b).evalf(subs={w1:w_0[0],w2:w_0[1],w3:w_0[2],b:w_0[3]})

        sum_diff_loss_w1 += (diff_loss_w1)**2
        sum_diff_loss_w2 += (diff_loss_w2)**2
        sum_diff_loss_w3 += (diff_loss_w3)**2
        sum_diff_loss_b += (diff_loss_b)**2

        sum_diff_loss = [sum_diff_loss_w1,sum_diff_loss_w2,sum_diff_loss_w3,sum_diff_loss_b]

        diff_loss = [diff_loss_w1,diff_loss_w2,diff_loss_w3,diff_loss_b]
        diff_loss_abs = [abs(diff_loss_w1),abs(diff_loss_w2),abs(diff_loss_w3),abs(diff_loss_b)]

        if  max(diff_loss_abs) <= 10E-6:
            break

        epoch += 1
        epochs.append(epoch)
        for i in range(4):
            w_0[i] = w_0[i] - learning_rate * diff_loss[i] / math.sqrt(sum_diff_loss[i]/epoch)    #Adagrad梯度下降
        loss_value.append(loss.evalf(subs={w1:w_0[0],w2:w_0[1],w3:w_0[2],b:w_0[3]}))
    print(w_0)
    plt.plot(epochs,loss_value,'black')
    plt.show()
gradicent_descent()

（Pycharm实现）

因为这不是一元线性回归，所以没有办法可视化y关于其feature的关系式。

但我们在梯度下降的过程中，可以将迭代的epoch数和对应loss的值记录下来，最后得到如下图形：

（这里可以发现，我们可以适当优化代码，使得loss funtion的迭代到4000的时候就停下来，这会大大节省时间）

以上demo主要包含以下核心点：

1. 最小二乘(这个是第一种方法，我后面又用了梯度下降。相比之下，梯度下降更为普遍与适用)
2. numpy库等的使用。
3. 数据集应该分为训练集与测试集。这样我们可以测试我们模型的误差。（这里当时想到了一个十折交叉验证，碍于时间，并未实现）
4. Adagrad算法实现。原理很简单，关键是如何将数学符号转换为Python语言。
   
   （以上均可以自行学习。李宏毅ML课程，周志华<<西瓜书>>，Bishop等）

个人感觉代码还有很多地方亟待优化，碍于时间，这里仅做记录。日后抽出时间修改完善。谢谢。



转载请注明出处，不作赘述。