作为数学系的一名学生,我们第一次接触莫比乌斯带是在《数学分析》三里面学习第二型曲面积分关于曲面的侧部分,在那里我们第一次了解到什么是单侧曲面,那么什么是单侧曲面呢?我们通常遇到的曲面大多是双侧曲面,单侧曲面的一个典型例子是
莫比乌斯(Mobius)带
。
MATH
01
莫比乌斯带的发现
这种曲面首先由德国数学家莫比乌斯发现得到,当莫比乌斯将纸袋放在地上后,正巧有几只蚂蚁爬在了上面,让莫比乌斯感到奇怪的是,蚂蚁并没有从纸的边缘翻跃,但却从一面爬到了另外一面。莫比乌斯十分惊讶,为何原本只有两个面的纸条,经过这样的折叠之后只有一个面了呢?这恰巧就是莫比乌斯带的神奇之处。

/莫比乌斯/
02
莫比乌斯带的构造
我们通常遇到的曲面大多是双侧曲面.单侧曲面的一个典型例子是默比乌斯(Mobius)带.它的构造方法如下:取一矩形长纸条ABCD(如图(a)),将其一端扭转180°后与另一端粘合在一起(即让A与C重合,B与D重合,如图(b)所示).
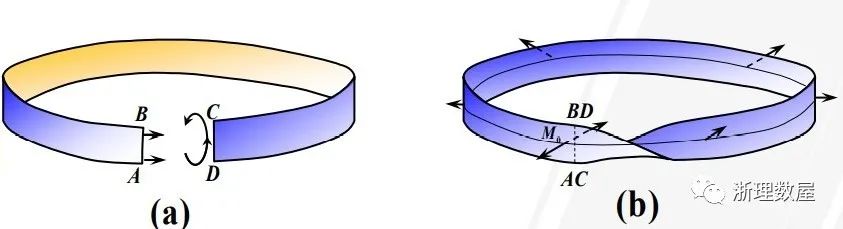
03
莫比乌斯带的拓展
如果沿着这条纸袋的中间画一条线,就会发现这条线可以平滑的从正面画到背面,这会使人产生一种错觉,那就是这两个“面”似乎在一个平面内,维度变为了0。如果我们将旋转算作一种维度,那么单单从莫比乌斯带的结构来看,莫比乌斯带包含一个水平360度的维度,还有一个垂直方向360度的维度,再加上这个纸带本身长宽的维度,那么此时的莫比乌斯带就有了四个维度!
原本是二维的一个平面,经过简单的旋转拼接之后,竟然产生了如此特殊的效果。这仅仅是它表面体现出的性质,那么它有哪些更为深刻的意义呢?
首先,我们来看一下克莱因瓶的构造过程:
准备一张纸
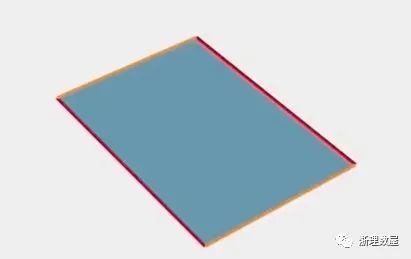
将红边闭合在一起,得到如下的管状物:
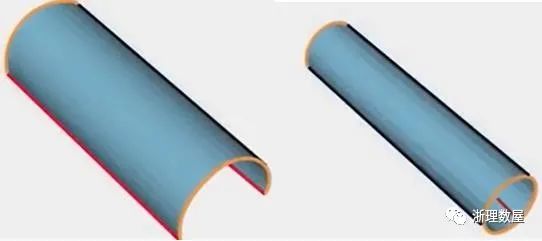
将黄圈以一种特殊的方式连接在一起,其中一个黄圈不断向外扩展,如下图所示:

这样便得到了克莱因瓶
实际上,克莱因瓶就是莫比乌斯带进行了某种延伸,所以另一种得到克莱因瓶的方法如下。
首先构造一个莫比乌斯带,然后我们将这个莫比乌斯带进行拉伸
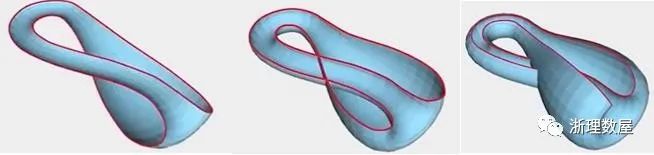
准备一张纸通过不断地拉伸我们就得到了克莱因瓶
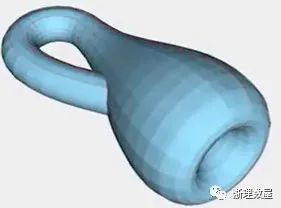
克莱因瓶的特点是它一条边都没有,就像球面一样也没有边,是一个闭合的曲面。但是克莱因瓶在我们的现实世界里并不存在,是一个存在于三维世界的四维物体,属于强行存在于四维空间的一种物体。
04
莫比乌斯带的启示
莫比乌斯带由于它本身的特殊性质,我们会想,我们的宇宙是否也有这种特性?我们让一个人沿着莫比乌斯带环游一周,最后发现了一件申请的事情,当这个人绕了一圈返回时,发现他竟然成为了最初出发时的镜像。在我们的宇宙中,类似的理论也会有可能发生,也许我们去宇宙旅行,返回时自己也会变为自己的镜像,理论上是有可能的,这大概是许多数学家对克莱因瓶执着研究的原因吧。
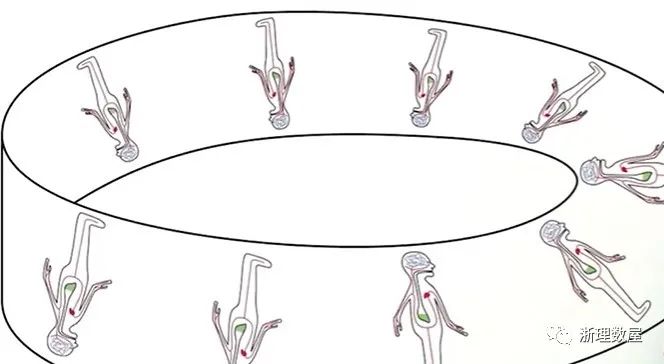
或许我们的宇宙就好比一条莫比乌斯带,宇宙的外部或许就是宇宙的内部,就像莫比乌斯带的交点一样,是一个循环往复的空间,可能我们不管如何寻找,都不会找到宇宙的边界,是不是很有意思?当然,这些只是科学家的猜想,真实情况究竟是怎样,还需我们不断探索。

05
莫比乌斯带的应用
莫比乌斯带在生活中被广泛地应用到了建筑,艺术,工业生产中。例如车站、工厂的传送带就做成了“莫比乌斯带”状结构,这样不仅可以增大皮带磨损的面积,还可以使应力分布到“两面”,从而延长一倍的使用周期;另外,计算机的打印机色带也做成了莫比乌斯带结构;除此外,运用莫比乌斯带原理可以建造立交桥和道路,避免车辆行人的拥堵;还有就是,在游乐园中的过山车也是运用莫比乌斯带的特性,来使过山车在轨道两面通过。


参考文献:
华东师范大学《数学分析》
莫比乌斯带有多神奇?一张纸却有四个维度,能否解释宇宙奥秘?
https://b23.tv/Q9qjXq
如果想了解更多数学内容和相关教学信息
欢迎关注本公众号”浙理数屋”

