设
f
(
x
)
f(x)
f
(
x
)
在节点
a
≤
x
0
,
x
1
,
⋯
,
x
n
≤
b
a\le x_0, x_1,\cdots,x_n\le b
a
≤
x
0
,
x
1
,
⋯
,
x
n
≤
b
处的函数值为
f
0
,
f
1
,
.
.
.
,
f
n
f_0,f_1,…,f_n
f
0
,
f
1
,
.
.
.
,
f
n
,设
P
(
x
)
为
f
(
x
)
P(x)为f(x)
P
(
x
)
为
f
(
x
)
在区间
[
a
,
b
]
[a,b]
[
a
,
b
]
上的具有一阶导数的插值函数
(1)若要求
P
(
x
)
P(x)
P
(
x
)
在
[
a
,
b
]
[a,b]
[
a
,
b
]
上具有一阶导数(一阶光滑度)
P
(
x
i
)
=
f
(
x
i
)
=
f
i
P
′
(
x
i
)
=
f
′
(
x
i
)
=
f
′
,
i
=
0
,
1
,
.
.
.
,
n
P(x_i)=f(x_i)=f_i\\ P'(x_i)=f'(x_i)=f’, i=0,1,…,n
P
(
x
i
)
=
f
(
x
i
)
=
f
i
P
′
(
x
i
)
=
f
′
(
x
i
)
=
f
′
,
i
=
0
,
1
,
.
.
.
,
n
P
(
x
)
P(x)
P
(
x
)
可以是最高次数为2n+1次多项式,两个节点就可以用
2
×
1
+
1
=
3
2\times 1+1=3
2
×
1
+
1
=
3
次多项式作为插值函数。
(2)同样,若要求
P
(
x
)
在
[
a
,
b
]
P(x)在[a,b]
P
(
x
)
在
[
a
,
b
]
上具有m阶导数(m阶光滑度),即
P
(
x
)
P(x)
P
(
x
)
在节点
x
0
,
x
1
,
.
.
.
,
x
n
x_0,x_1,…,x_n
x
0
,
x
1
,
.
.
.
,
x
n
处必须满足:
P
(
x
i
)
=
f
(
x
i
)
=
f
i
P
′
(
x
i
)
=
f
′
(
x
i
)
=
f
i
′
⋯
P
(
m
)
(
x
i
)
=
f
(
m
)
(
x
i
)
=
f
i
(
m
)
,
i
=
0
,
1
,
.
.
.
,
n
P(x_i)=f(x_i)=f_i\\ P'(x_i)=f'(x_i)=f’_i\\ \cdots\\ P^{(m)}(x_i)=f^{(m)}(x_i)=f^{(m)}_i, i=0,1,…,n
P
(
x
i
)
=
f
(
x
i
)
=
f
i
P
′
(
x
i
)
=
f
′
(
x
i
)
=
f
i
′
⋯
P
(
m
)
(
x
i
)
=
f
(
m
)
(
x
i
)
=
f
i
(
m
)
,
i
=
0
,
1
,
.
.
.
,
n
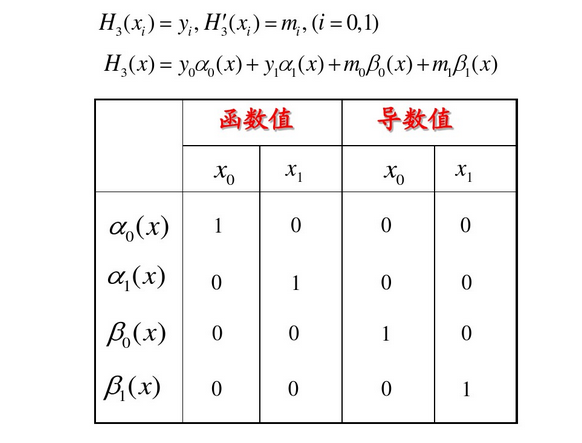
定义:称满足(1)或(2)式的插值问题为Hermite插值,称满足(1)或(2)式的插值多项式
P
(
x
)
P(x)
P
(
x
)
为Hermite插值多项式,记为
H
k
(
x
)
H_k(x)
H
k
(
x
)
,k为多项式次数。
三次Hermite插值






三次Hermite插值余项
R
3
(
x
)
=
f
(
4
)
(
ξ
)
4
!
(
x
−
x
0
)
2
(
x
−
x
1
)
2
,
x
0
≤
ξ
≤
x
1
R_3(x)=\frac{f^{(4)}(\xi)}{4!}(x-x_0)^2(x-x_1)^2,x_0\le \xi\le x_1
R
3
(
x
)
=
4
!
f
(
4
)
(
ξ
)
(
x
−
x
0
)
2
(
x
−
x
1
)
2
,
x
0
≤
ξ
≤
x
1
当
f
(
4
)
(
x
)
在
[
x
0
,
x
1
]
f^{(4)}(x)在[x_0,x_1]
f
(
4
)
(
x
)
在
[
x
0
,
x
1
]
上存在时,上述公式成立。
#例题

