世界上主流的集成电路都是在硅片上制作的,而其中用的最多的技术就是CMOS
为了理解集成电路,我们必须先了解集成电路所用的原料的性质
1. 硅原子的结构
每个硅原子最外层有四个电子,我们称他们为价电子(Valence electrons)
高纯度的硅拥有近乎完美的晶体结构(crystalline structure),是用来制作微处理器的绝佳材料,这并
不便宜
,但已经是性价比最高的选择了
晶体结构,也可以称为晶体,意味着原子之间形成的化学键在空间中周期性排列
在晶体硅中
,每个原子与其它四个原子形成共价键(covalent band)
根据原子力学,原子为围绕其原子核的电子提供了离散能级(discrete energy level)
电子会优先占据低能级,每个能级能够承载的电子是有限的,比如最低级1s最多就只能承受两个电子
对于单个硅原子,它的能级是离散的,一群孤立不互相影响的原子的能级也是离散的
那么问题来了,如果我们将众多硅原子连在一起,会发生什么事呢?
2. 能带的形成
在一个硅晶体中,大概有
1 0 23 10^{23}
1
0
2
3
个硅原子在他们之间形成了化学键,因此,他们的离散能级结合形成了能带(energy band)
注意,能级上承载的是电子,因此能带上也都是电子,整个能带带负电,能级越高代表携带的电子能量越大,但在最底层有一些空穴是带正电的
能量的参数包括其在半导体中的位置和电子的动量,平时我们不是太需要关注动量,除非发生光电效应
一个电子的动能为
p = h k / ( 2 π ) p=hk/(2\pi)
p
=
h
k
/
(
2
π
)
,其中h是普朗克常数
在工程领域,我们常用能带及其所在的位置作为绘图时的横坐标
2.1 能带图
要理解半导体的电子性质,我们必须要理解能带图(energy band diagrams)
一个传统的能带图包含顶端的导带(conduction band)和底端的价带(valence band),在他们中间存在带隙(band gap),图示如下:
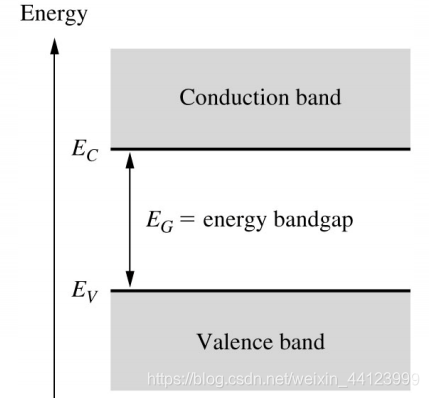
上图横坐标代表的是位置
导带中大多数位置都是空缺的,只有一部分被
电子
占据,如果温度高于0K,导带中的电子可以在空缺位置间自由移动
价带中大多数位置都是填充的,只有一部分是空缺的,这些空缺被称为
空穴
(holes),当电子在其中移动时,看起来就像是空穴在移动
我们一般不关心导带中的空穴和价带中的电子
导带和价带中间的带隙不含能级,我们一般称它为半导体的能带隙(energy band gap),通常带隙中也不含电子
室温下,硅的带隙大概为1.1eV
在温度为绝对零度0K时,所有的电子都将去到能级最低的地方,这就意味着价带中充满了电子,而导带中不含电子
当温度升高,T>0K时,价带中的一些电子会获得能量从而突破带隙进入导带
在温度为室温300K时,导带中会有一些电子,而价带中会有一些空穴
整个过程中电子的数量是守恒的
半导体的性质可以说就是由导体中空穴和电子的浓度决定的,我们称单位体积的电子为n,单位体积的空穴为p,控制p和n我们就控制了半导体的电学特性
在画能带图时,我们可以将其简化为几条线,如图:
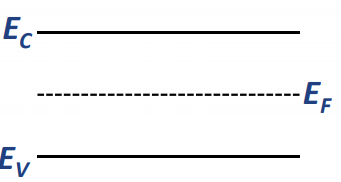
上方的水平线代表的是导带的最低端,下方的水平线代表的是价带的最顶端,中间代表的是费米能级(Fermi level)
2.2 费米能级
费米能级的位置与电子与空穴的数量有关
,这句话从何而来呢?
首先,在能带图中,越低的能级就越有可能被电子占据,其中被电子占据的概率为二分之一的能级就被称为费米能级,至于为什么这个能级可以出现在不允许电子占据的带隙中,则要牵扯到量子态,此处不多赘述,只要知道费米能级并非是一个实际的能级,而是某种象征。
总之,知道费米能级处电子占据的概率为二分之一,那么一个地方的电子越多,能带被占据的概率就越大,费米能级就会越靠近导带,相对的,如果一个地方的电子越少,空穴越多,就代表能带被占据的概率越小,费米能级就会越靠近价带
3. 掺杂
通过外部引入一些电子或者空穴,也就是掺杂(doping),我们可以控制n和p
这些引入的原子通常为磷原子或硼原子,引入的杂质被称为掺杂物(dopant)
选用的原子建立的能级通常靠近
E V E_V
E
V
或
E C E_C
E
C
,在硅中,掺入磷会建立靠近
E C E_C
E
C
的能级,如图:
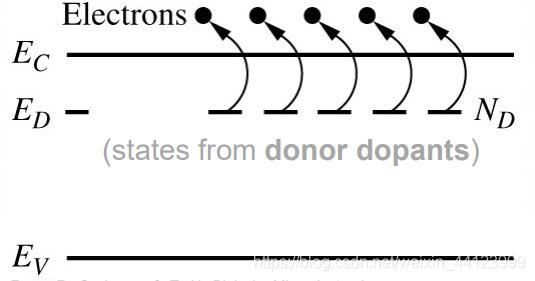
其中
E D E_D
E
D
就是磷引入的能级,
因为
E D E_D
E
D
里
E C E_C
E
C