问题:
若x=1,2,3与y=2,4,6一一对应,那么当x等于4时,y等于?
解决过程:
与上一篇文章相同,仍是设定线性模型f(x)=wx+b,但这次的w,我们会用梯度下降的办法来求出最适值。
梯度的定义:
假设现在有一条二次函数,那么梯度就是在某一个点的导数,

假设初始的猜想w为图中的红点,那么可得该点的梯度为正,且由图可得,若要求得最小的损失值,则红点应该向左移动,即w应该减小。同理若红点在最小损失值左侧,则x应该增大。
由此可得每次更新的w = w – α*g,g为该点的导数,若g>0,则w减小,若g<0,则w增大。
α为学习率,可以理解为每次w更新的幅度大小,若α取值过大,则可能出现跳过最小值点过多的情况,如下图
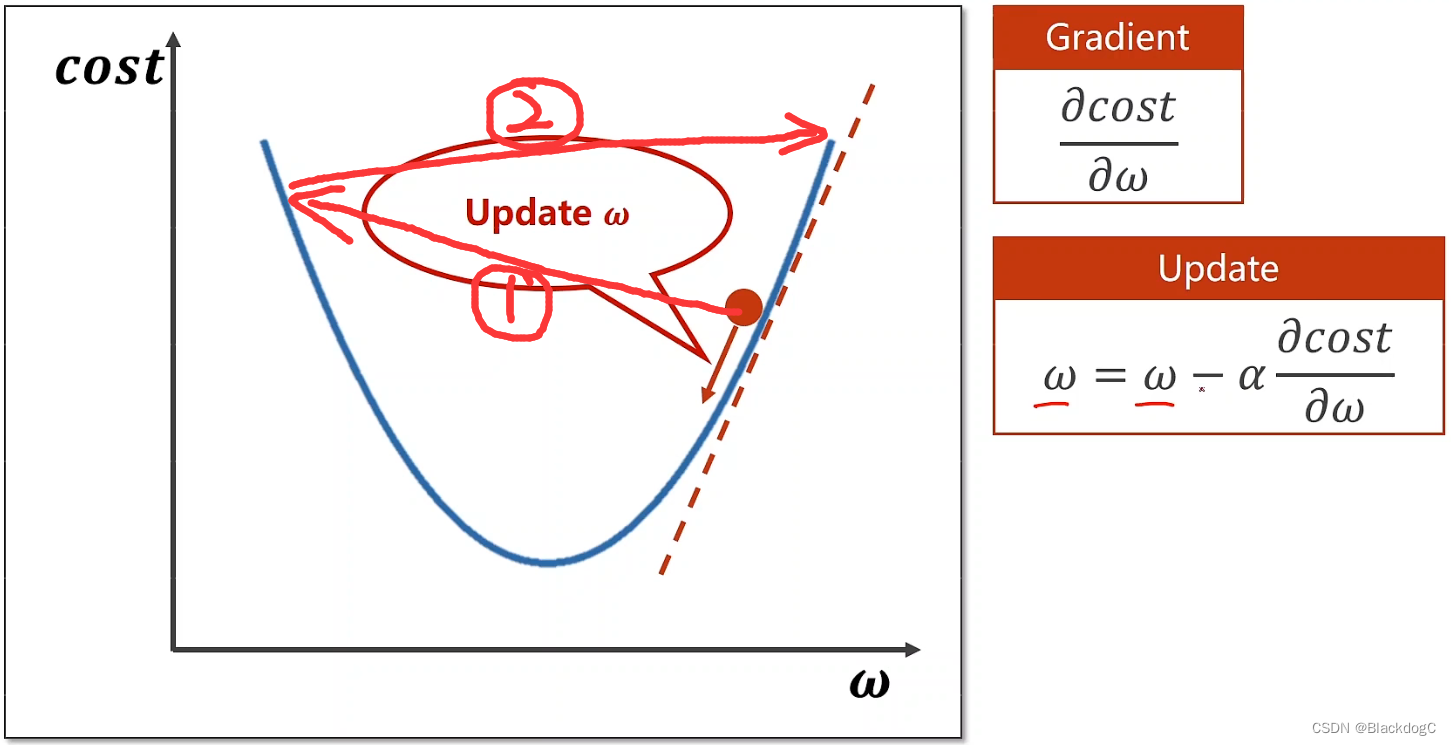
但是若α的取值过小,则会出现效率缓慢,只寻找到局部最低点等问题。

在上图的非凸函数中,就只找得到局部最低点。
所以α的取值需要多次尝试,尽量得到最合适的值。
公式推导:
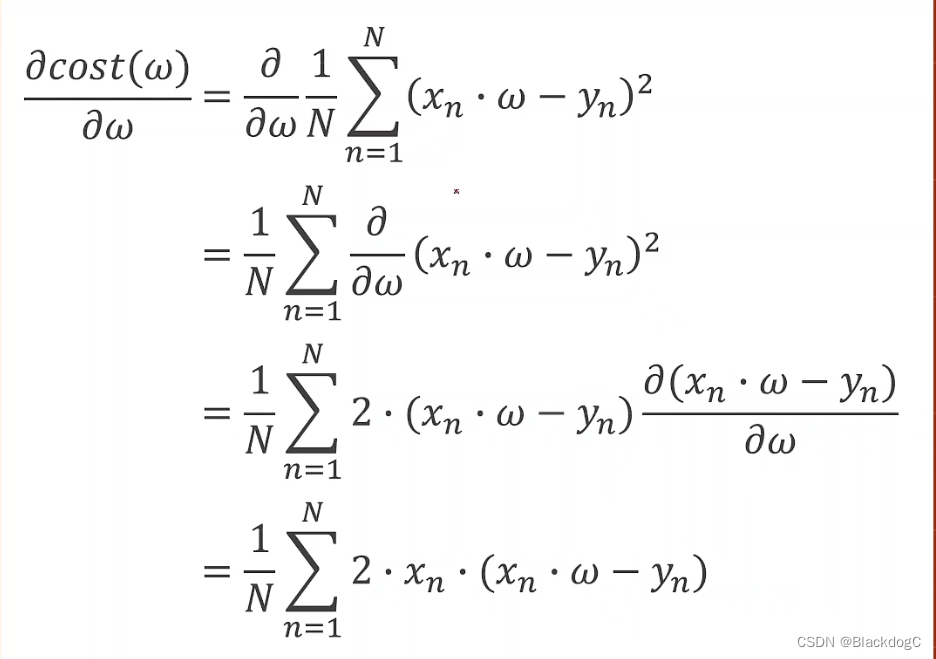
代码实现过程:
import numpy as np
import matplotlib.pyplot as plt
from regex import W
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
w = 1.0
cost_list = []
epoch_list = []
def forward(x):
return x*w
def cost(xs,ys):
cost = 0
for x,y in zip(xs,ys):
y_pred = forward(x)
cost +=(y_pred - y)**2
return cost / len(xs)
def gradient(xs,ys):
grad = 0
for x,y in zip(xs,ys):
grad +=2*x*(x*w-y)
return grad/len(xs)
print ('predict (before training)', 4, forward(4))
for epoch in range (100) :
cost_val = cost(x_data,y_data)
grad_val = gradient(x_data,y_data)
w -= 0.01 * grad_val
print('epoch:', epoch, 'w=', w, 'loss=', cost_val)
epoch_list.append(epoch)
cost_list.append(cost_val)
print ('predict (after training)', 4, forward(4))
plt.plot(epoch_list,cost_list)
plt.ylabel(cost)
plt.xlabel(epoch)
plt.show()
打印图标:

鞍点:
若一条直线出现了g = 0 的情况,如下图

那么由公式w = w – α*g,此时g = 0,w将不再更新,但并未达到最低点
或者在更高维的视角下,从不同角度观测时有出入,如下图:

从两个角度来看,一个时最低点,一个是最高点,这也成为鞍点。
解决办法:随机梯度更新
由整个样本相加改为单个样本
代码实现如下:
import numpy as np
import matplotlib.pyplot as plt
from regex import W
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
w = 1.0
loss_list = []
epoch_list = []
def forward(x):
return x*w
def loss(x,y):
y_pred = forward(x)
return (y_pred-y)**2
def gradient(x,y):
return 2*x*(x*w-y)
print ('predict (before training)', 4, forward(4))
for epoch in range (100) :
for x,y in zip(x_data,y_data):
grad = gradient(x,y)
w = w - 0.01*grad
print("\tgrad:",x,y,grad)
l = loss(x,y)
epoch_list.append(epoch)
loss_list.append(l)
print ('predict (after training)', 4, forward(4))
plt.plot(epoch_list,loss_list)
plt.ylabel(loss)
plt.xlabel(epoch)
plt.show()
打印图标:
