RMQ – ST表
1、RMQ 简介
-
RMQ (Range Minimum / Maximum Query)
问题是指:对于长度为
nn
n
的数列
AA
A
,回答若干询问
(A
,
i
,
j
)
(A, i, j)
(
A
,
i
,
j
)
(1
≤
i
,
j
≤
n
)
(1≤i,j≤n)
(
1
≤
i
,
j
≤
n
)
,返回数列 A 中区间在
[i
,
j
]
[i,j]
[
i
,
j
]
中的最小 (大) 值所在的下标。也就是说,
RM
Q
RMQ
R
M
Q
问题是指求区间最值的问题。 -
RM
Q
RMQ
R
M
Q
总体来说还是动态规划的思想,相对比较独立的算法,不需要太深的程序和算法基础,而且相对好理解!
个人理解
:
- 解决区间 上简单的静态问题
朴素 RMQ
-
以区间最小值为例,对于区间
[l
,
r
]
[l, r]
[
l
,
r
]
,从第
ll
l
个元素枚举到第
rr
r
个元素,将值最小的元素的下标存储在变量
id
x
idx
i
d
x
上,一旦遇到比记录的元素小的就更新
id
x
idx
i
d
x
的值,枚举完所有
r−
l
+
1
r-l+1
r
−
l
+
1
个元素后,得到最小值所在的下标。int QueryMinIndex(int l, int r) { int idx = l; for(int i = l + 1; i <= r; ++i) { if(A[i] < A[idx]) { idx = i; } } return idx; } -
我们发现这个算法的时间复杂度,最坏情况下就是
l=
1
,
r
=
n
l = 1,r = n
l
=
1
,
r
=
n
的情况,为
O(
n
)
O(n)
O
(
n
)
。 -
当询问比较频繁的时候,这个算法的时间复杂度是无法满足要求的。
RMQ – ST 算法
-
ST
(
S
p
a
r
s
e
T
a
b
l
e
)
ST(Sparse Table)
S
T
(
S
p
a
r
s
e
T
a
b
l
e
)
算法是基于动态规划的,之前在说到动态规划的时候,有个很重要的概念就是状态。 - 求解区间最大值可以通过所有数字增加一个负号转化成求区间最小值问题,所以这里我们可以只讨论区间最小值问题。
-
这个算法也利用到了状态的概念,用 f[i][j] 表示起点为
jj
j
,长度为
2i
2^i
2
i
的区间内的最大值所在下标。通俗的讲,f[i][j]f[i][j] 就是区间
[j
,
j
+
2
i
)
[j, j + 2^i)
[
j
,
j
+
2
i
)
内的最大值的下标(注意:这里表示的区间为左闭右开)。
对于长度为
16
16
1
6
的数组,
f
[
i
]
[
j
]
f[i][j]
f
[
i
]
[
j
]
所表示的区间如下:
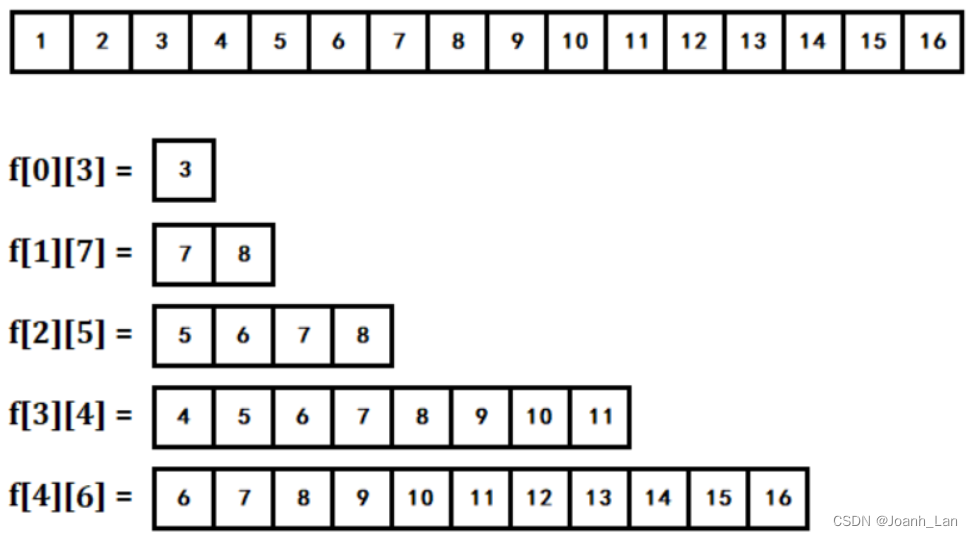
-
由于区间
[j
,
j
+
2
i
)
[j, j + 2^i)
[
j
,
j
+
2
i
)
长度为
2i
2^i
2
i
,如果
i>
0
i > 0
i
>
0
,那么它可以分解成两个长度为
2i
−
1
2^{i-1}
2
i
−
1
的区间,即:
[j
,
j
+
2
i
)
=
[
j
,
j
+
2
i
−
1
)
+
[
j
+
2
i
−
1
,
j
+
2
i
)
[j, j + 2^i) = [j, j + 2^{i-1}) + [j + 2^{i-1}, j + 2^i)
[
j
,
j
+
2
i
)
=
[
j
,
j
+
2
i
−
1
)
+
[
j
+
2
i
−
1
,
j
+
2
i
)
-
当
i=
3
,
j
=
4
i=3, j = 4
i
=
3
,
j
=
4
时,有
[4
,
12
)
=
[
4
,
8
)
+
[
8
,
12
)
[4, 12) = [4,8) + [8,12)
[
4
,
1
2
)
=
[
4
,
8
)
+
[
8
,
1
2
)
,更加直观的
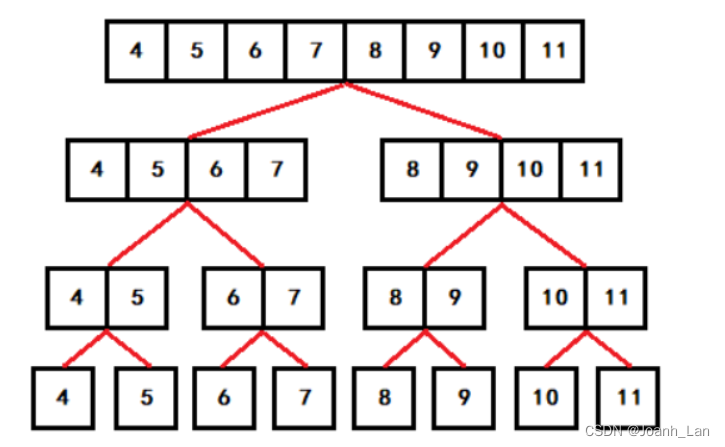
int RMQ_MinIndex(ValueType A[], int l, int r) {
return A[r] < A[l] ? r : l;
}
-
这个函数在传参时需要保证
l≤
r
l \le r
l
≤
r
,并且由于数组长度并不一定是 2 的幂,所以
rr
r
有可能超出数组长度,所以调用方需要进行边界判断; -
通过这个函数,可以得到
f[
i
]
[
j
]
f[i][j]
f
[
i
]
[
j
]
的状态转移方程如下:
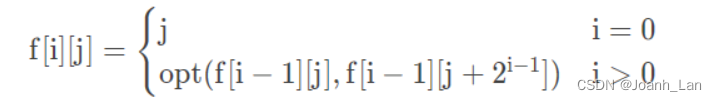
-
其中
op
t
opt
o
p
t
就是
RMQ_MinIndex
函数;
ST表实际上就是DP
注:
个人习惯不同,
i
,
j
i,j
i
,
j
表示的意义不同(下面与上面正好相反),根据个人习惯进行code就行
预处理 ST表
for (int i = 1; i <= n; i++)
st[i][0] = s[i];
for (int i = 1; i <= 20; i++)
for (int j = 1; j + (1 << i) - 1 <= n; j++)
st[j][i] = max(st[j][i - 1], st[j + (1 << (i - 1))][i - 1]);
-
f[
i
]
[
j
]
f[i][j]
f
[
i
]
[
j
]
的状态数目有多少呢? -
由于
i<
=
l
o
g
(
n
)
,
j
<
=
n
i <= log(n),j<=n
i
<
=
l
o
g
(
n
)
,
j
<
=
n
,所以总的状态数为
nl
o
g
(
n
)
nlog(n)
n
l
o
g
(
n
)
,每次状态转移的时间复杂度为 O(1),所以预处理总时间为
O(
n
l
o
g
(
n
)
)
O(nlog(n))
O
(
n
l
o
g
(
n
)
)
。
询问
-
f[
i
]
[
j
]
f[i][j]
f
[
i
]
[
j
]
的计算只是做了一步预处理,但是我们在询问的时候,不能保证每个询问区间长度都是
22
2
的幂,如何利用预处理出来的值计算任何长度区间的值就是我们接下来要解决的问题。 -
区间长度等于
11
1
的情况最小值就等于它本身; -
区间长度大于
11
1
时,即给定任意区间
[a
,
b
]
(
1
≤
a
<
b
≤
n
)
[a, b] (1 \le a < b \le n)
[
a
,
b
]
(
1
≤
a
<
b
≤
n
)
,必定可以找到两个区间
XX
X
和
YY
Y
,它们的并是
[a
,
b
]
[a, b]
[
a
,
b
]
,并且区间
XX
X
的左端点是
aa
a
,区间
YY
Y
的右端点是
bb
b
,而且两个区间长度相等,且都是 2 的幂。[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iOPhE0PK-1671893490468)(C:\Users\ASUS\AppData\Roaming\Typora\typora-user-images\image-20221224182929924.png)]
-
设区间长度为
2k
2^k
2
k
,则
XX
X
表示的区间为
[a
,
a
+
2
k
)
[a, a + 2^k)
[
a
,
a
+
2
k
)
,
YY
Y
表示的区间为
(b
−
2
k
,
b
]
(b – 2^k, b]
(
b
−
2
k
,
b
]
,则需要满足一个条件就是
XX
X
的右端点必须大于等于
YY
Y
的左端点减一,即
a+
2
k
−
1
≤
b
−
2
k
a+2^k-1 \le b-2^k
a
+
2
k
−
1
≤
b
−
2
k
,通过移项得到: -
2k
+
1
≥
(
b
−
a
+
1
)
2^{k+1} \ge (b-a+1)
2
k
+
1
≥
(
b
−
a
+
1
)
-
两边取对数(以2为底),得
k+
1
≥
l
o
g
2
(
b
−
a
+
1
)
k+1 \ge log_2(b-a+1)
k
+
1
≥
l
o
g
2
(
b
−
a
+
1
)
,最后得到:
k≥
l
o
g
2
(
b
−
a
+
1
)
−
1
k \ge log_2(b-a+1) – 1
k
≥
l
o
g
2
(
b
−
a
+
1
)
−
1
-
所以这里,
kk
k
只要需要取最小的满足条件的整数即可,
b−
a
+
1
b-a+1
b
−
a
+
1
的取值为
[2
,
n
]
[2, n]
[
2
,
n
]
,可以通过预处理把所有
kk
k
求出来。 -
当
lo
g
2
v
log_2v
l
o
g
2
v
为整数时,
k=
l
o
g
2
v
−
1
k = log_2v – 1
k
=
l
o
g
2
v
−
1
;否则
kk
k
为
lo
g
2
v
−
1
log_2v – 1
l
o
g
2
v
−
1
的上整。
int query(int l, int r)
{
int renk = log2(r - l + 1);
return max(st[l][renk], st[r - (1 << renk) + 1][renk]);
}
板子
#include <bits/stdc++.h>
#define buff \
ios::sync_with_stdio(false); \
cin.tie(0);
//#define int long long
using namespace std;
const int N = 100010;
int st[N][21];
int s[N];
int n, q;
int query(int l, int r)
{
int renk = log2(r - l + 1);
return max(st[l][renk], st[r - (1 << renk) + 1][renk]);
}
void solve()
{
cin >> n >> q;
for (int i = 1; i <= n; i++)
cin >> s[i];
for (int i = 1; i <= n; i++)
st[i][0] = s[i];
for (int i = 1; i <= 20; i++)
for (int j = 1; j + (1 << i) - 1 <= n; j++)
st[j][i] = max(st[j][i - 1], st[j + (1 << (i - 1))][i - 1]);
while (q--)
{
int l, r;
cin >> l >> r;
cout << query(l, r) << '\n';
}
}
int main()
{
buff;
solve();
}