一、简介及打开方式
cftool工具箱可以将数据点拟合成曲线或曲面并直观显示出图像。能实现多种类型的线性、非线性曲线/面拟合。
有两种方式打开cftool:(1)在命令行窗口输入”cftool”并回车;(2)在MATLAB的”APP”选项栏中找到”Curve Fitting”程序打开即可。
二、使用方法
1、数据导入
界面左上部分为数据区域,下拉框中会自动识别MATLAB工作区中的数组,选中需要拟合的X和Y数据即可,若选择X、Y、Z三组数据则可以拟合三维曲面。此外,还可以自定义不同数据的权值,同样将数据在Weights中选中即可。
2、拟合方法
界面上方可以选择不同的拟合方法,二维图像的拟合方法有:
(1)
Custom Equations
:自定义函数拟合。
(2)
Exponential
:指数函数拟合,默认形式:f(x) = a*exp(b*x),在”Number of terms”中可以选择指数项的个数,范围1~2。
(3)
Fourier
:傅里叶级数逼近,默认形式:f(x) = a0 + a1*cos(x*w) + b1*sin(x*w),在”Number of terms”中可以选择公式中正余弦项的个数,范围1~8。
(4)
Gaussian
:高斯逼近,默认形式:f(x) = a1*exp(-((x-b1)/c1)^2),在”Number of terms”中可以选择公式中指数项的个数,范围1~8。
(5)
Interpolant
:插值。有以下4种类型:
Nearest neighbor
(最近邻)、
Linear
(线性插值)、
Cubic spline
(三次样条插值)、
Shape-preserving(PCHIP)
(分段三次Hermite插值)。
其中,样条插值仅需要被插值函数在插值节点处的函数值,不需要知道被插值函数在插值节点处的导数值,数据要求低,光滑性好,可以达到二阶导数连续,但数据变化过大时曲线可能出现波动。Hermite插值是分段三次多项式插值,需要同时知道被插值函数在插值节点处的函数值和导数值,数据要求高,可以达到一阶导数连续,光滑性不如样条插值的好,但其具有保形性,不会出现局部波动。以下这个例子可以很明显的看出二者区别:
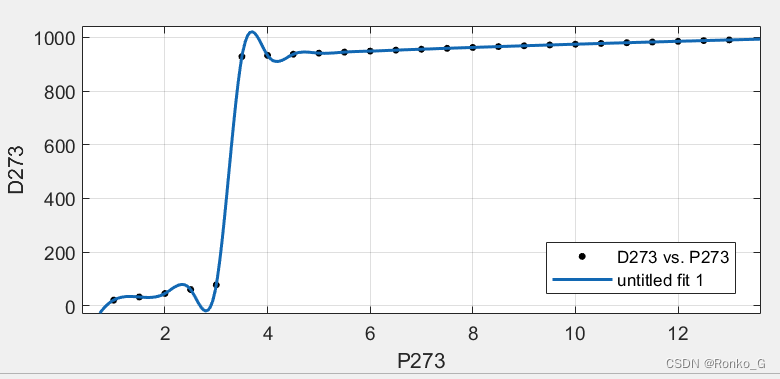
三次样条插值

分段三次Hermite插值
(6)
Linear Fitting
:线性组合拟合。默认形式:f(x) = a*(sin(x-pi)) + b*((x-10)^2) + c。本质是将各种不同类型的函数进行线性组合。在”Edit”中可以自定义各线性项的权重和形式。
(7)
Polynomial
:多项式函数拟合。默认形式:f(x) = p1*x + p2,即最常见的线性最小二乘拟合。在”Degree”中可以选择多项式的最高次数,范围1~9。
(8)
Power
:幂函数拟合。默认形式:f(x) = a*x^b。在”Number of terms”中可以选择是否加常数项,若选择2,则公式变为:f(x) = a*x^b+c。
(9)
Rational
:有理数逼近。默认形式:f(x) = (p1) / (x + q1)。公式的分子和分母均为多项式,在”Numerator degree”中可以选择分子多项式最高次数,范围0~5。在”Denomenator degree”中可以选择分母多项式最高次数,范围1~5,且x最高次项的系数只能为1。
(10)
Smoothing Spline
:平滑样条。这种方法的具体原理较为复杂,MATLAB定义了一个代价函数RSS来衡量拟合误差,拟合时会使此RSS值尽可能小。函数形式如下。前半部分用来衡量拟合曲线与原数据的近似程度,后半部分用来衡量曲线的光滑程度。
应用时,权重wi若没有给定则默认均为1,平滑系数p的取值为 [0,1]。总的来说,p值越小,拟合曲线越平滑,但与原数据误差越大;p值越大,曲线越倾向于经过所有数据点,但局部可能会出现波动。
(11)
Sum of Sin
:正弦逼近。默认形式:f(x) = a1*sin(b1*x+c1)。其通过一串正弦函数来逼近数据点,在”Number of terms”中可以选择正弦函数的个数,范围1~8。
(12)
Weibull
:威布尔分布,形式为:f(x) = a*b*x^(b-1)*exp(-a*x^b)。统计学中常用于元件寿命估计。
三、拟合效果评价
窗口左侧的”Results”部分显示函数模型、参数的拟合值以及部分评价参数,主要有:
(1)
SSE
:拟合误差平方和,接近0,表示与数据拟合好,但是要小心过拟合(过于贴合数据点而使曲线波动较大);
(2)
R-square
:数据点与拟合值之间的相关系数平方值,趋近于1说明约相关,拟合效果好;
(3)
RMSE
:均方差(标准差)。同样此值越小,说明拟合效果越好。
四、注意事项
(1) 工具箱上方有按钮可以调节图例、网格、坐标轴范围:

(2) 对于同一组数据,参数范围不同,其拟合结果也可能差距很大。如果拟合效果不好,可以在”Fit Options”中调整参数的初始值、上下限,往往会在一定程度上改善结果。所以,设置好待拟合函数的参数的StartPoint,Lower和Upper三者的值可以使拟合更加准确。
如,用自定义函数y=k/(1+exp(a+b*x))来拟合一组数据,如果采用程序默认的k初始值0.5502,拟合结果为:

如果将k的初始值改为800,则拟合结果变为:

可以看到,拟合结果有明显变化。