Pytorch torch.nn.KLDivLoss
首先是KL散度损失的计算公式
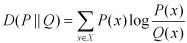
再对应到pytorch中的描述(0.4.0版本),这里的描述是
l
o
g
y
n
−
x
n
logy_n-x_n
l
o
g
y
n
−
x
n
而不是
l
o
g
(
y
n
−
x
n
)
log(y_n-x_n)
l
o
g
(
y
n
−
x
n
)
,由此可知对于输入
x
n
x_n
x
n
,输入必须是概率的log形式。通常做法是通过logsoftmax函数对输出做处理变换到概率然后转换到log空间。
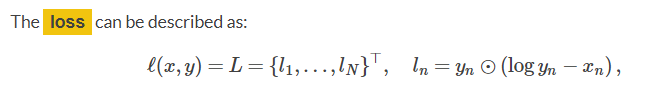
假设输入x大小为(MXCXWXH),y的大小也为(MXCXWXH),N是M
C
W*H的乘积,最后计算N个
l
n
l_n
l
n
, 也就是每一个位置的KL散度。如果reduce=True,最后会呈现加法或者平均的结果
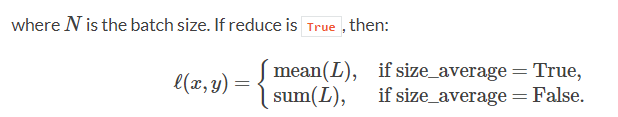
如果reduce=False
那么就输出大小为(MXCXWXH)。
loss = nn.KLDivLoss(reduce=False)
batch_size = 5
log_probs1 = F.log_softmax(torch.randn(batch_size, 10), 1)
probs2 = F.softmax(torch.randn(batch_size, 10), 1)
loss(log_probs1, probs2) / batch_size
reduce=False输出的大小是5*10,reduce=True输出的大小是1
torch.nn.LogSoftmax
Applies the Log(Softmax(x)) function to an n-dimensional input Tensor. The LogSoftmax formulation can be simplified as
LogSoftmax
(
x
i
)
=
log
(
exp
(
x
i
)
∑
j
exp
(
x
j
)
)
\text{LogSoftmax}(x_{i}) = \log\left(\frac{\exp(x_i) }{ \sum_j \exp(x_j)} \right)
LogSoftmax
(
x
i
)
=
lo
g
(
∑
j
exp
(
x
j
)
exp
(
x
i
)
)
torch.nn.BCELoss和 torch.nn.KLDivLoss的联系
KL散度相对于BCE损失有很大区别。对于BCE用于关节点回归分类还是很常见,当
y
n
=
1
y_n=1
y
n
=
1
时候,等式
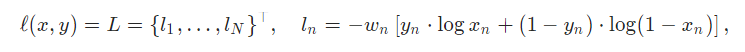
最小化
−
l
o
g
(
x
n
)
-log(x_n)
−
l
o
g
(
x
n
)
,当
y
n
=
0
y_n=0
y
n
=
0
时候,等式最小化-log(1-x_n)
如果将散度应用在joint的回归分类任务上,当
y
n
=
1
y_n=1
y
n
=
1
时候,等式
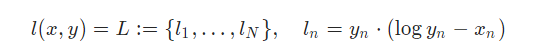
最小化-
x
n
x_n
x
n
,也即
−
l
o
g
(
x
n
)
-log(x_n)
−
l
o
g
(
x
n
)
.如果
y
n
=
0
y_n=0
y
n
=
0
,上式不优化。
综上所述,二者在
y
n
=
1
y_n=1
y
n
=
1
的时候是完全等价的。