近日刷了很多二分法相关的题目,想以一文简单总结一下
文章目录
-
1.二分查找经典框架
-
2.题型一:给定一个特定的target然后在数组中寻找
-
3.题型二:给定一个限定的值(最大,最小)而且无法直接在数组中找到,只能通过大致判断在哪个区间,然后缩小查找范围
-
4.题型三:答案二分
1.二分查找经典框架
- 1.相邻就退出 start + 1<end
- 2.求中点要防溢出
- 3.三种情况分开写
- 4.双重检查更保险
public static int binarySearch(int[] nums, int target) {
// write your code here
if (nums == null || nums.length == 0){
return -1;
}
int start = 0;
int end = nums.length - 1;
//要素1.相邻就退出 start + 1<end
while (start + 1<end){
// mid = (start + end) /2 这种写法在大多数情况下是对的
// 但是如果 start = 2^31 -1 end = 2^32 - 1 明显这会发生一个整数溢出
// 要素2.求中点要防溢出
int mid = (end - start)/2 + start;
// 要素3.三种情况分开写
if (nums[mid] == target){
return mid; //这里的写法要根据题目来 如果是找到并返回, 则此处可以直接返回
// end = mid; //如果是找满足target的第一个位置 则这里继续往前面找
//start = mid; //如果是找满足target的最后一个位置 则此处继续往后找
}else if(target < nums[mid]){
//在左区间
end = mid;
}else {//在右区间
start = mid;
}
}
// 要素4.双重检查更保险
if (nums[start] == target){
return start;
}
if (nums[end] == target){
return end;
}
return -1;
}
2.题型一:给定一个特定的target然后在数组中寻找
2.1 First/Last Position
2.1.1First Position(lintcode14)
给定一排序数组,其中元素可能重复,给定一目标数,寻找该目标数在数组中首次出现的位置
First Position
- 非常清晰的二分法的应用,寻找最开始的,所以往最前面找
-
关键点
if (nums[mid] == target){ //寻找最开始的位置 所以往前找 end = mid; ........... //因为找最开始的位置,所以先检查前面的位置 if (nums[start] == target){ return start; } if (nums[end] == target){ return end; } - 完整代码
*/
public static int binarySearch02(int[] nums, int target) {
if (nums == null || nums.length == 0){
return -1;
}
int start = 0;
int end = nums.length - 1;
//1.相邻就退出
while (start+1<end){
//2.求中点 放溢出
int mid = (end - start)/2 + start;
//3.三种情况分别判断
if (nums[mid] == target){
//寻找最开始的位置 所以往前找
end = mid;
}else if (target<nums[mid]){
end = mid;
}else {
start = mid;
}
}
//4.二次判断更保险
if (nums[start] == target){
return start;
}
if (nums[end] == target){
return end;
}
return -1;
}
2.1.2First Bad Version(lintcode74)
寻找第一个坏的版本,思路和2.1几乎完全一样,,都是寻找第一个满足条件的。需要注意的点也都一样
第一个坏的版本
- 完整代码
public int findFirstBadVersion(int n) {
// write your code here
//可利用二分查找来解决
//如果每次查找 中点是坏的 则往前找
//如果每次查找 中点是好的 则往后找
//这里要注意这里不是数组下标
int start = 1;
int end = n;
while (start + 1 < end){
int mid = (end - start)/2 + start;
//如果中点对应版本是坏的 返回true 则继续往前半部分找
if (SVNRepo.isBadVersion(mid)){
end = mid;
}else {
//如果中点对应版本是好的 返回false 则继续往后半部分找
start = mid;
}
}
//二次判断
//从while中退出时 start 和 end一定是相邻的
//那么显然这两个之中 一定有一个是坏的 但是题目求最近的那一个
//所以先验证start
//如果不行 则一定是end
if (SVNRepo.isBadVersion(start)){
return start;
}
return end;
}
2.2 Last Position(lintcode458)
和First Position刚好相反,寻找满足添加的最后一个数。那关键的地方也正好相反。
Last Position
-
首先要注意,找到满足添加的点后继续往后半部分找
int mid = (end - start)/2 + start; if (target == nums[mid]){ //由于这里是寻找 最后一个等于target的位置, 显然应该尽可能的往后面找(这里和First position的区别) //所以如果当前的mid = target的话 则继续往后寻找 start = mid; } -
其次就是最后判断的时候先判断end
//因为是找最后一个 所以先判断后者 if (nums[end] == target){ return end; } if (nums[start] == target){ //start 和 end一定相邻,如果其中一个不等于目标 则最后的一个一定是start return start; } return -1; -
完整代码
public static int lastPosition(int[] nums, int target) { // write your code here if (nums == null || nums.length == 0){ return -1; } int start = 0; int end = nums.length -1; while (start +1 < end){ int mid = (end - start)/2 + start; if (target == nums[mid]){ //由于这里是寻找 最后一个等于target的位置, 显然应该尽可能的往后面找(这里和First position的区别) //所以如果当前的mid = target的话 则继续往后寻找 start = mid; }else if (target < nums[mid]){ end = mid; }else { start = mid; } } //因为是找最后一个 所以先判断后者 if (nums[end] == target){ return end; } if (nums[start] == target){ //start 和 end一定相邻,如果其中一个不等于目标 则最后的一个一定是start return start; } return -1; }
2.3寻找插入位置(leetcode35)
二分法的简单应用,在给定数组中寻找给定的target,如果找到则返回位置,如果没找到则返回该目标数应该插入的位置,插入后数组仍然有序。
寻找插入位置
-
1.首先两种特殊情况的判断,如果给定数小于数组的最小值和大于数组的最大值,则插入位置是固定的。
//首先判断两种特殊的情况 if(target < nums[0]){ return 0; } if(target > nums[nums.length - 1]){ return nums.length; } -
2.如果找到,则显然可以直接返回位置
int mid = (end - start)/2 + start; // 要素3.三种情况分开写 循环内部不返回 if (nums[mid] == target){ return mid; } -
3.跳出while继续判断,此时start 和 end一定相邻,先判断start是否与之相等,如果不等,则end也不可能与之相等,则返回应该插入的位置,显然应该是end的所在位置。
if (target == nums[start] ){ return start; } //这里就是处理 在给定数组的中间寻找 找不到的情况 那么target 一定是处于 start 和end之间 //之间的(因为相邻即退出)那么 要返回插入的位置 一定是end return end; -
4.完整代码
if (nums == null || nums.length == 0){ return -1; } //首先判断两种特殊的情况 if(target < nums[0]){ return 0; } if(target > nums[nums.length - 1]){ return nums.length; } int start = 0; int end = nums.length - 1; //要素1.相邻就退出 start + 1<end while (start + 1<end){ // mid = (start + end) /2 这种写法在大多数情况下是对的 // 但是如果 start = 2^31 -1 end = 2^32 - 1 明显这会发生一个整数溢出 // 要素2.求中点要防溢出 int mid = (end - start)/2 + start; // 要素3.三种情况分开写 循环内部不返回 if (nums[mid] == target){ return mid; }else if(target < nums[mid]){ //在左区间 end = mid; }else {//在右区间 start = mid; } } // 要素4.双重检查更保险 //下面两种if是能找到的情况 则正常返回 if (target == nums[start] ){ return start; } //这里就是处理 在给定数组的中间寻找 找不到的情况 那么target 一定是处于 start 和end之间 //之间的(因为相邻即退出)那么 要返回插入的位置 一定是end return end; }
2.4区间查找(leetcode34)
给的数组和目标数,查找目标数在数组中的起始位置。
区间查找
-
完全就是
2.1
和
2.3
的一个结合 -
完整代码
public int[] searchRange02(int[] nums, int target) { int[] rs = {-1,-1}; if (nums == null || nums.length == 0){ return rs; } rs[0] = findFirst(nums, target); rs[1] = findLast(nums, target); return rs; } /** * 20190802 * 找到满足条件的第一个位置 * @param nums * @param target * @return */ public static int findFirst(int[] nums, int target){ int start = 0; int end = nums.length - 1; while (start +1 <end){ int mid = (end - start)/2 + start; if (target == nums[mid]){ //往前找 end = mid; }else if (target > nums[mid]){ //往后找 start = mid; }else { end = mid; } } if (target == nums[start]){ return start; } if (target == nums[end]){ return end; } return -1; } /** * 20190804 * 找最后一个位置 * @param nums * @param target * @return */ public static int findLast(int[] nums, int target){ int start = 0; int end = nums.length - 1; while (start +1 <end){ int mid = (end - start)/2 + start; if (target == nums[mid]){ //往后找 start = mid; }else if (target > nums[mid]){ //往后找 start = mid; }else { end = mid; } } if (target == nums[end]){ return end; } if (target == nums[start]){ return start; } return -1; }
2.5 Search in a Big Sorted Array(lintcode447)
给定一个很大的升序正数数组,不能求长度,但是可以通过一个函数返回第k个数的值。要求在log(k)的时间内找到指定target的值
- 不能求长度,二分法的end的初始值如何确定?
- end的值可以不等于整个数组的长度,只要大于target即可
- 那么,只要我能找到一个index,它在数组中对应的值大于target,也就可以确定end的初始值
-
所以,关键就在于
如何在log(k)的时间内找到大于target的index
-
倍增法
:一次寻找 1 2 4 8 …
2n
2^n
2
n
- 只要确定了end的初始值,后面的则是一个普通的二分查找问题了
-
完整代码
/** * 20190804 * 显然,这道题目需要二分法来解决 * 但是 因为不能求长度,而无法直接为 end赋值 * 其实 end的值 不一定是需要整个数组长度的 * nums[end] 只要 > target即可 * 所以关键点 如何在log(k)的时间内 能找到一个nums[end] 则成为了关键 * 这里介绍一种“倍增”的思想 就是找1,找不到就找2 然后找4!! * @param reader: An instance of ArrayReader. * @param target: An integer * @return : An integer which is the index of the target number */ public int searchBigSortedArray(ArrayReader reader, int target){ //1利用倍增法 寻找end的最大值 //即找到第一个 大于target 的 index值即可 int index = 1; while (reader.get(index - 1) < target ){ index = index * 2; } //只要找到了index 下面就是一个普通的二分查找了 int start = 0; int end = index - 1; while (start + 1< end){ int mid = (end - start)/2 + start; if (reader.get(mid) == target){ //因为这里要找 First,所以继续往前找 不能返回 end = mid; }else if (target > reader.get(mid)){ start = mid; }else { end = mid; } } if (reader.get(start) == target){ return start; } if (reader.get(end) == target){ return end; } return -1; }
2.6 搜索二维矩阵(leetcode74)
给定一二维数组,其中每一行从左到右是升序,而且下一行的第一个数大于上一行的最后一个数,也就是按每一行排列,整个二维数组的值都是升序
- 本质还是二分法的应用,关键在于把二维的数组转换为一维数组,然后进行二分查找
2.6.1解法一:先确定目标数所在行,然后在该行进行二分查找
/**
* 20190805(自解AC)
* 关键在于如何把2D转换为1D 然后进行二分查找
* @param matrix 给定矩阵
* @param target 给定搜索的数
* @return
*/
public static boolean searchMatrix(int[][] matrix, int target) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0){
return false;
}
int row = matrix.length;
int col = matrix[0].length;
int target_row = 0;
for (int i=0;i<row; i++){
//按行 遍历 找到target所在的行
if (target>=matrix[i][0] && target<=matrix[i][col-1]){
target_row = i;
}
}
//这里已经把2D转换为了1D直接 利用二分查找即可
//对target_row 行 进行二分查找
int start = 0;
int end = col - 1;
while (start+1<end){
int mid = (end - start)/2 + start;
if (matrix[target_row][mid] == target ){
return true;
}else if (matrix[target_row][mid] < target){
start = mid;
}else {
end = mid;
}
}
if (target == matrix[target_row][start]){
return true;
}
if (target == matrix[target_row][end]){
return true;
}
return false;
}
2.6.2解法2
- 和解法1没有本质区别
-
关键在于一个知识点:
在一个m*n的数组中,第k个数的位置是[k/n][k%n]
- 又因为整个数组的数按行排列起来都升序的,因此可以直接在整个数组中进行二分查找
/**
* 20190805
* 参考:https://yisuang1186.gitbooks.io/-shuatibiji/search_a_2d_matrix.html
* 其实和我的解法 没有本质上的差别,仍然是把2D转换为1D
* 但是关键的地方在于如和转换 这里的转换方法感觉比我的优雅
* 给定 m*n的数组 第k个数 在其中的位置为 [k/n][k%n]
* 知道了这个 就可以查找了
* @param matrix
* @param target
* @return
*/
public static boolean searchMatrix02(int[][] matrix, int target){
if (matrix == null || matrix.length == 0 || matrix[0].length == 0){
return false;
}
int row = matrix.length;
int col = matrix[0].length;
int start = 0;
int end = row * col - 1;
while (start + 1 < end){
int mid = (start) + (end - start)/2;
if (matrix[mid/col][mid%col] == target){
return true;
}else if (matrix[mid/col][mid%col] < target){
start = mid;
}else {
end = mid;
}
}
if (matrix[start/col][start%col] == target){
return true;
}
if (matrix[end/col][end%col] == target){
return true;
}
return false;
}
2.7 搜索二维矩阵II(leetcode240,lintcode38)
给定二维矩阵,该二维矩阵有如下特性:
每行中的整数从左到右是排序的。
每一列的整数从上到下是排序的。
在每一行或每一列中没有重复的整数。
给定一目标数,要求返回该数在矩阵中的出现次数lintcode。
-
此题在两个网站上的描述略有不同,lintcode要求返回出现
target
的次数,leetcode要求返回是否存在该
target
。 - 显然litcode的要求更高一点,因此以lintcode为准
2.7.1解法一
-
因为每一行或者每一列都是有序的,完全可以遍历行或者列,然对每一列或者行进行二分搜索,时间复杂度为
O(
n
l
o
g
(
m
)
)
\mathcal{O}(nlog(m))
O
(
n
l
o
g
(
m
)
)
或者
O(
m
l
o
g
(
n
)
)
\mathcal{O}(mlog(n))
O
(
m
l
o
g
(
n
)
)
2.7.2解法二
-
要进一步缩小时间复杂度,则考虑线性的复杂度
O(
n
)
\mathcal{O}(n)
O
(
n
)
- 显然从时间复杂度的角度看不能使用二分法了
- 那么只能把该二维数组当作一个整体去考虑
/**
* 20190806
* @param matrix
* @param target
* @return
*/
public int searchMatrix(int[][] matrix, int target) {
// write your code here
if (matrix.length == 0 || matrix[0].length == 0){
return 0;
}
int m = matrix.length;//行数
int n = matrix[0].length;//列数
//从 最后一行的第一个元素开始搜索
int x = m-1;
int y = 0;
//只要不越界
int count = 0;
while (x>=0 && y<n){
//如果在当前位置 找到这样的一个target
if (matrix[x][y] == target){
count++;
//则继续往右上搜索
//从上到下增 从左到右增 则[x][y] = target的时候 只可能[x--][y++]的方向可能还有一个值等于target
x--;
y++;
continue;
}else if (matrix[x][y] < target){
//小了 则往大的方向搜索
y++;
}else {
//大了 往小的地方搜索
x--;
}
}
return count;
}
3.题型二:给定一个限定的值(最大,最小)而且无法直接在数组中找到,只能通过大致判断在哪个区间,然后缩小查找范围
3.1 Find Minimum in Rotated Sorted Array寻找旋转排序数组中的最小值(leetcode153,lintcode159)
给定一旋转的排序数组,要求找到其中的最小值。例如:Input: [3,4,5,1,2] Output: 1
-
首先一个很直白的思路,就是一个for循环嘛,遍历整个数组,只要找到第一个
nums[i]>nums[i+1]
,则就是最小值,时间复杂度为
O(
n
)
\mathcal{O}(n)
O
(
n
)
-
如果想把一个
O(
n
)
\mathcal{O}(n)
O
(
n
)
的继续做优化的话,只能到
O(
l
o
g
n
)
\mathcal{O}(logn)
O
(
l
o
g
n
)
,而且几乎只能用二分法 -
这道题还非常明显的告知了
有序数组
,所以几乎应该用二分来做了
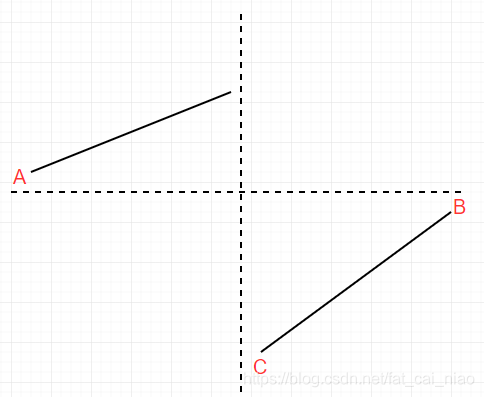
-
这道题的结构,可以用这个图很清晰的表达出来,显然A点和B点的值都是可以获取的
A = nums[0],B=nums[nums.length-1]
-
C
点的值明显就是最小值,那如何求得C点的值呢? -
二分法中一定会涉及到一个
目标数
,这里也一样,只是这里要求的是
小于等于目标数的第一个位置上的数
,取等号是因为可能原数组只旋转一位,则原来最小的第一位跑到了最后一位 -
所以这里选B作为目标数,
寻找<=B的First position
即可 - 后面用二分法解即可
- 完整代码
public static int findMin(int[] nums) {
if(nums == null || nums.length == 0){
return -1;
}
//定义 target
int target = nums[nums.length-1];
//下面的工作就变成寻找 小于target的第一个数
//当然也是用二分法寻找
int start = 0;
int end = nums.length - 1;
while (start + 1 < end){
int mid = (end - start)/2 + start;
//如果当前终点位置 的值 小于等于 target
// 则当前的mid 一定在旋转后数组 的后一段了
// 因为数组是旋转过的 target一定是 后一段的最大值
// 当前的mid位置 小于 target则一定是在后半段了(前半段的值一定都大于target)
// 为了找到小于target的第一个位置 则继续往前找
if (nums[mid] <= target ){
end = mid;
}else {
//如果 当前中点的值 大于target 则显然小于target的值肯定还在后面
// 这是因为数组是旋转过的 target一定是 后一段的最大值
// 当前还有比target大的 则说明当前的位置一定在前一段 所以继续往后找
start = mid;
}
}
if (nums[start] <= target){
return nums[start];
}
//给定排序数组中的最小值是一定存在的
return nums[end];
}
3.2Search in Rotated Sorted Array在旋转排序数组中搜索(leetcode33)
给定一个旋转的排序数组,和一个目标数
targte
,在旋转排序数组中查找该
targte
,找到返回其位置,未找到返回
-1
。
3.2.1解法一
- 根据第6题的思路,可以找到旋转排序数组中的最小值
- 很明显,该最小值把旋转排序数组划分为两个有序区间
- 然后在这个两个有序区间内做二分查找即可。
/**
*20190805
* 受今天leetcode153题得启发
* 可以先找到最小得那个数
* 然后就可以把数组分成两个有序的部分了
* 然后对这两个有序的部分进行二分查找即可
*/
public int search02(int[] nums, int target) {
if (nums == null || nums.length == 0){
return -1;
}
//先利用153的思路找到旋转点的位置
//也就是 数组中最小的那个数的位置
int pivot = 0;
//数组中的最后一个数
int lastNumber = nums[nums.length - 1];
int start = 0;
int end = nums.length - 1;
//二分查找寻找pivot
while (start + 1 < end){
int mid = (end - start)/2 + start;
if (nums[mid] <= lastNumber){
end = mid;
}else {
start = mid;
}
}
//这里因为找最小 则一定存在 不是start 就是end
if (nums[start] <= lastNumber){
pivot = start;
}else{
pivot = end;
}
//分别在两个区别找
int rs0 = findPivot(nums,0,pivot,target);
int rs1 = findPivot(nums,pivot, nums.length - 1, target);
if (rs0!=-1){
return rs0;
}
if (rs1!=-1){
return rs1;
}
return -1;
}
public static int findPivot(int[] nums, int start, int end, int target){
while (start +1< end){
int mid = (end - start)/2 + start;
if (target == nums[mid]){
return mid;
}else if (target > nums[mid]){
start = mid;
}else {
end = mid;
}
}
if (nums[start] == target){
return start;
}
if (nums[end] == target){
return end;
}
return -1;
}
3.2.2 解法2
- 给定的旋转排序数组一定存在两个有序区间
-
二分查找一定有三个位置
start mid end
-
根据抽屉原理,三个位置,两个区间,一定
至少有两个位置落在同一个有序区间
-
也就是说可以确定两个位置在一个确定的有序区间内,然后就可以确定
targte
是否落在这个有序区间内,然后就可以进一步缩小
targte
的可能位置
/**
* 20190806
* 另一种基于分类讨论的思想
* 旋转数组 一定存在两个有序区间,二分法中的 start mid end 一定有两个位置 落在同一个有序区间内(猛然想到这是组合数学里的很重要的抽屉原理)
* 那显然就分两种情况讨论了
* nums[mid] < nums[end] 那么显然 mid 和 end 一定在有序区间内 可能在前面 也可能在后面
* 而 start 的位置是不能确定的
* start---->mid---->end
*当mid 和 end 确定在同一个区间了 , 现在就可以确定 target 是否 落在 mid 和 end区间内了
* nums[mid] < target <= nums[end] 如果满足这个不等式 则start = mid 即可 进一步缩小targte所在的区间(这也是二分法的精髓
* 尽可能的缩小目标数所在区间)
*如果不满足 那target 一定在前面的区间 则为了进一步缩小区间 则 end = mid
*
* 上面是一种情况, 那如果 nums[mid] >= nums[end],逻辑是完全一样的
* 现在 start 和 mid 一定落在同一个有序区间内 那么先确定target是否在这个区间 在 就 end = mid
* 不在则 start = mid
* @param nums 给定数组
* @param target 给定target
* @return
*/
public static int search03(int[] nums, int target){
if (nums.length == 0){
return -1;
}
int start = 0;
int end = nums.length - 1;
while (start + 1 < end){
int mid = (end - start)/2 + start;
if (nums[mid] == target){
return mid;
}
//如果mid 和 end 在同一个有序区间内
if (nums[mid] < nums[end]){
//如果target落在 mid 和 end区间内
if (nums[mid]<target && target <= nums[end]){
//则往后缩小区间
start = mid;
}else {
end = mid;
}
}else {//如果start 和 mid 落在同一个有序区间内
//如果 target 落在 start 和 mid 之间
if (nums[start] <= target && target<nums[mid]){
//则往前缩小区间
end = mid;
}else {
start = mid;
}
}
}
if (nums[start] == target){
return start;
}
if (nums[end] == target){
return end;
}
return -1;
}
3.3 Maximum Number in Mountain Sequence山脉序列中的最大值(lintcode585)
给定一个整数数组,该数组是一个先增后减的序列,求序列中的最大值
-
一图胜千言
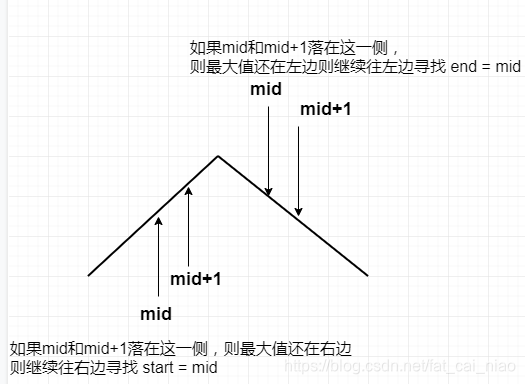
-
二分法的核心在于不断的缩小目标数所在的范围,一次能够抛弃掉一半的不可能位置,一步步缩小,直到可以用一个判断语句就把结果找出来。
/**
* 20190808
* @param nums: a mountain sequence which increase firstly and then decrease
* @return: then mountain top
*/
public static int mountainSequence(int[] nums) {
// write your code here
if (nums.length == 0){
return -1;
}
int start = 0;
int end = nums.length - 1;
while (start + 1 < end){
int mid = (end - start)/2 + start;
if (nums[mid] <= nums[mid + 1]){
start = mid;
}else {
end = mid;
}
}
if (nums[start] > nums[end]){
return nums[start];
}else {
return nums[end];
}
}
3.4 Find Peak Element寻找峰值(lincode75,leetcode162)
给定一个数组,满足一下条件
- 相邻位置的数字是不同的
- A[0] < A[1] 并且 A[n – 2] > A[n – 1]
- 假定P是峰值的位置则满足A[P] > A[P-1]且A[P] > A[P+1],返回数组中任意一个峰值的位置。
-
此题完全和上一题几乎一样的思路,只是此题的情况多了一种
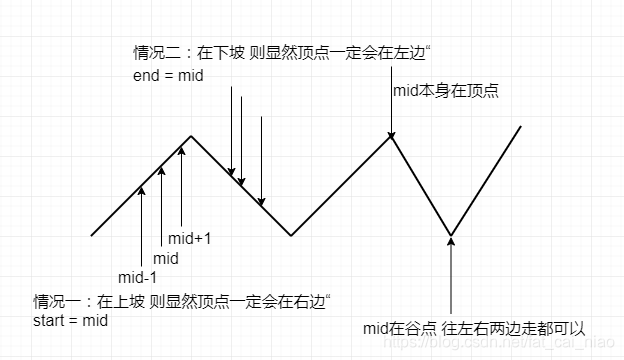
-
跳出while后,注意两种特殊情况的判断
if (start == 0){ return start; } if (nums[start-1] < nums[start] && nums[start] > nums[start+1]){ return start; } if (end == nums.length - 1){ return end; } if (nums[end - 1] < nums[end] && nums[end] > nums[end+1]){ return end; } -
完整代码
public int findPeakElement(int[] nums) { if (nums.length == 0){ return -1; } if (nums.length ==1){ return 0; } if (nums.length == 2){ if (nums[0]>nums[1]){ return 0; }else { return 1; } } int start = 0; int end = nums.length - 1; while (start +1 < end){ int mid = (end - start)/2 + start; //情况一 mid刚好在peak上 if (nums[mid-1] < nums[mid] && nums[mid] > nums[mid+1] ){ return mid; //情况2 mid 在上坡 顶点肯定在右边 }else if (nums[mid-1] < nums[mid] && nums[mid] < nums[mid+1]){ start = mid; //情况3 mid 在下坡 顶点肯定在左边 }else if (nums[mid-1] > nums[mid] && nums[mid] > nums[mid+1]){ end = mid; }else { //情况4 mid 在谷点 则往两边走都可以 end = mid; } } //说明 start 没有改变 而上述while循环都是往最大的区间跑 说明start就是最大值 //下方的end同理 if (start == 0){ return start; } if (nums[start-1] < nums[start] && nums[start] > nums[start+1]){ return start; } if (end == nums.length - 1){ return end; } if (nums[end - 1] < nums[end] && nums[end] > nums[end+1]){ return end; } return -1; }
4.题型三:答案二分
此类题不会给出一个明确的数组和目标数,而是要经过分析发现满足某个条件的最大和最小,通过二分可以不断的逼近那个值。
4.1Sqrt(x) 求x的平方根(leetcode69)
给定一个整数,求其开平方以后向下取整的值
- 样例 2:
输入: 3
输出: 1
样例解释:
返回对x开根号后向下取整的结果。
-
本质上是求
小于
x的平方根的
最大整数
-
如果把从
1
到
x
看做一个数组
[1,2,3,4,...,n]
-
则是求小于x的平方根的
最后一个整数
-
分析到这里就可以用二分来解决了
-
先确定二分的范围
start = 1,end= x
-
注意一个细节
,在做判断的时候不能写成
mid * mid > x
这样会造成溢出 -
全部代码
public static int mySqrt(int x) { if (x == 0){ return 0; } //确定二分的范围 int start = 1; int end = x; while (start + 1 < end){ int mid = (end - start)/2 + start; //如果当前中点 大于x的平方根 显然继续往前找 if (mid > Math.sqrt(x)){ end = mid; }else { //小于等于 x的平方根 则往后找,因为我们要找最大的那个数 start = mid; } } if (end <= Math.sqrt(x)){ return end; } return start; }
4.2Wood cut 木材加工(lintcode183)
给定一个数组,数组的每一个元素值代表木材的长度;给定一个
k
,要求将每一根木材进行切分,切分出来的小木材的数量至少为
k
,而且每根小木材的长度要
最大
。
- 木材长度为整数
- 如果无法切分成k个,则返回0
L = [232, 124, 456]
k = 7
Output: 114
-
首先要明白求的答案是什么
-
求的是木材切分的
长度
,这个长度要满足两个条件-
按照这个长度切,切分出来的木材数量至少为k(>=k)
-
显然满足条件1的长度有很多,我们要求所有满足条件1的长度里最大的一个,换个角度看,就是这个长度+1就不满足条件1了
-
-
明确了要求的答案是什么,接下来要明确
答案可能存在的范围
-
start=1
,也就是按长度为1来切分,这样显然会大于k -
end = max(L)
,按数组元素的最大值来切,则至少能切出k=1 -
接下来就可以不断的用二分法来缩小答案所在的区间
-
如果按当前长度mid来切,切出来的数量大于等于
k
,说明mid太小了,数量多了,则增大长度mid -
如果按当前长度mid来切,切出来的数量小于k,说明mid大了,数量少了,则减少长度k
-
代码:
public int woodCut(int[] L, int k) { if (L.length== 0){ return 0; } // write your code here //排序是为了方便后面求最大值 Arrays.sort(L); //确定答案可能存在的区间 //最小值 按长度为1 来切 则一定满足条件 int start = 1; // 最大值按max(L)来切 这样至少满足k=1; int end = L[L.length-1]; while (start + 1 < end){ int mid = (end - start)/2 + start; if (count(L, mid)>=k){ //如果按长度mid 来切分出来的数量 大于等于K //说明 mid 太小了 切分出来的太多了 所以需要增大mid start = mid; }else { //如果按 长度mid切分出来的数量 小于等于k // 说明mid 有点大了 end = mid; } } //因为求最大的长度 所以先验证end if (count(L, end) >= k){ return end; } if (count(L, start) >= k){ return start; } return 0; } public static int count(int[] L, int length){ int sum = 0; for (int x:L){ sum += (x/length); } return sum; }
4.3Copy Books(lintcode437)
给定一个数组,数组的长度代表书的数量,数组的元素代表每一本书的页数。给定一个数k,代表有k个人来复印这些书,复印一本书的时间就等于这本书的页数,一个人可以复印多本书,但是这多本书必须是连续的。k个人同时开始复印这些书,要求的是复印完所有的书的最少时间。
pages = [3, 2, 4], k = 2
5
题意描述得有点复杂了,拿一个具体实例来说,三本书,每本的页数如数组所示,两个人来复印,问复印完所需要的最少的时间。
两个人来复印三本书,显然有两种分法 [3,2][4] 和 [3] [2,4]
按前面的分法 至少只需要5分钟 而后面至少需要6分钟
所以就是 k个人同时来分n本书,有很多种不同的分法,需要从这不同中分法中找出
所花时间最少的
分法,让k个人能完成n本书的复制
-
因为每本书复制所花的时间就是页数,所以上题可以进一步解释为
给定含有n个元素的数组,和一个整数k,将数组分成k份,
,显然分法有很多种,假设有m种,每一种分法里都有一个子数组最大值,我们要在这
m个最大值里求一个最小值
-
注意我们要求的是时间,满足两个条件
- 这个时间保证k个人都能把书复印完
- 这个时间是在所有可能的时间组合里最小的
-
同样先确定范围
-
这个时间最小 肯定就是
max(array)
,按这个时间来分 可以保证
k = len(array)
个人复印完所有的书 -
最大是
sum(array)
, 按这个时间份,可以办证
k =1
个人复印完所有的书 -
显然 时间减少, 则需要更多的人来复印
-
时间增多 则需要更少的人来复印
public int copyBooks(int[] pages, int k) {
// write your code here
int max = 0;
int sum = 0;
for (int x :pages){
sum += x;
if (x > max){
max = x;
}
}
int start = max;
int end = sum;
while (start + 1 < end){
int mid = (end - start)/2 + start;
if (numberOfWorkers(pages, mid)>k){
//如果按照当前的时间分配 所需工人大于 k
//说明时间少了 则需要增加时间
start = mid;
}else {
//如果按照当前的时间分配 所需工人小于等于 k
//因为要求的时间是最少的 所以继续往前面找 看有不有更少的时间能满足
end = mid;
}
}
if (numberOfWorkers(pages, start) <= k){
return start;
}
return end;
}
/**
* 20190809
* 要理解这段程序 他的意义是求 在给定的时间下 求最少的人数来完成 n本书籍的复制
* @param pages
* @param t
* @return
*/
public static int numberOfWorkers(int[] pages, int t) {
int count = 0;
int sum = 0;
for (int i = 0; i < pages.length; i++) {
// 如果说 当前书籍所需要花的时间 和前面累加起来的时间 在时间t内 已经不能搞定了 则需要分配一个人手了
// 则从 j --- i-1 的书籍 都交给这个人来复印
// 而且同时 需要从当前这个i 重新开始累积了
if (sum + pages[i] > t) {
sum = pages[i];
count++;
} else {
//如果从 j 到 i 书籍的复印时间都 <= t 那说明 还不需要增加一个人手
//则继续累积时间
//这里的逻辑是因为要求的人数是最少的
//也就是说 我需要在给定的时间t内 尽可能的完成多的书籍的复制
sum += pages[i];
}
}
//这里需要+1的原因在于 如果前面刚好累积到最后一个 i=n-1 此时跳出循环了 但是从 j 到 n-1还没有分配人来复制
//所以这里需要一个人来复制
count++;
return count;
}