深度学习之自编码器(5)VAE图片生成实战
本节我们基于VAE模型实战Fashion MNIST图片的重建与生成。如下图所示,输入为Fashion MNIST图片向量,经过3个全连接层后得到隐向量
z
\boldsymbol z
z
的均值与方差,分别用两个输出节点数为20的全连接层表示,FC2的20个输出节点表示20个特征分布的均值向量
μ
\boldsymbol μ
μ
,FC3的20个输出节点表示20个特征分布的取
log
\text{log}
log
后的方差向量。通过
Reparameterization Trick采样
获得长度为20的隐向量
z
\boldsymbol z
z
,并通过FC4和FC5重建出样本图片。
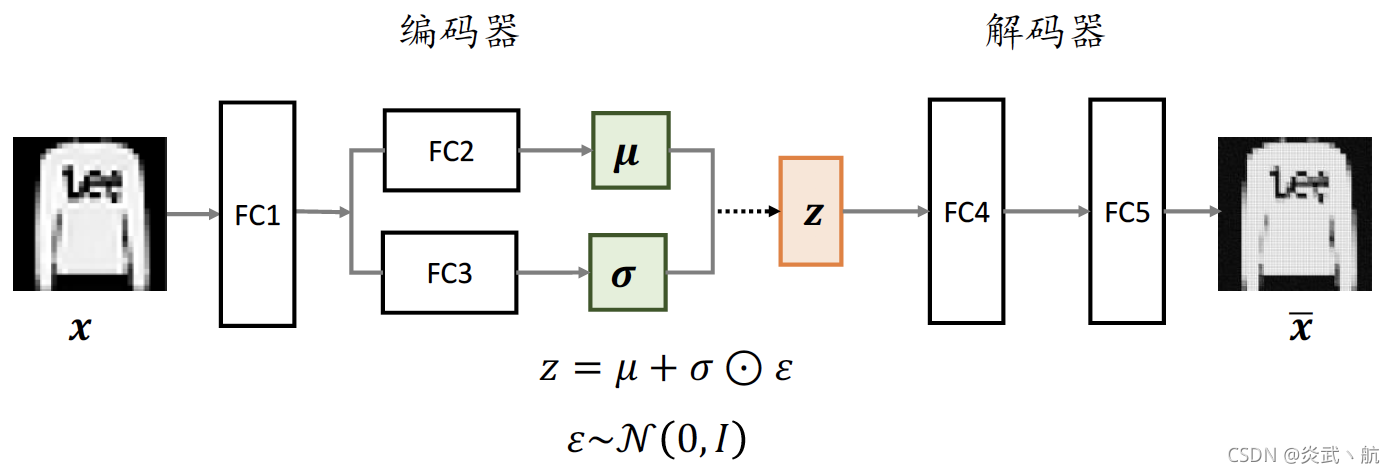
VAE模型结构
VAE作为生成模型,除了可以重建输入样本,还可以单独使用解码器生成样本。通过从先验分布
p
(
z
)
p(\boldsymbol z)
p
(
z
)
中直接采样获得隐向量
z
\boldsymbol z
z
,经过解码后可以产生生成的样本。
1. VAE模型
我们将Encoder和Decoder子网络实现在VAE大类中,在初始化函数中,分别创建Encoder和Decoder需要的网络层。代码如下:
class VAE(keras.Model):
# 变分自编码器
def __init__(self):
super(VAE, self).__init__()
# Encoder网络
self.fc1 = layers.Dense(128)
self.fc2 = layers.Dense(z_dim) # get mean prediction
self.fc3 = layers.Dense(z_dim)
# Decoder网络
self.fc4 = layers.Dense(128)
self.fc5 = layers.Dense(784)
Encoder的输入先通过共享层FC1,然后分别通过FC2与FC3网络,获得隐向量分布的均值向量与方差的
log
\text{log}
log
向量值。代码如下:
def encoder(self, x):
# 获得编码器的均值和方差
h = tf.nn.relu(self.fc1(x))
# 获得均值向量
mu = self.fc2(h)
# 获得方差的log向量
log_var = self.fc3(h)
return mu, log_var
Decoder接受采样后的隐向量
z
\boldsymbol z
z
,并解码为图片输出。代码如下:
def decoder(self, z):
# 根据隐藏变量z生成图片数据
out = tf.nn.relu(self.fc4(z))
out = self.fc5(out)
# 返回图片数据,784向量
return out
在VAE的前向计算过程中,首先通过编码器获得输入的隐向量
z
\boldsymbol z
z
的分布,然后利用Reparameterization Trick实现的reparameterize函数采样获得隐向量
z
\boldsymbol z
z
,最后通过解码器即可恢复重建的图片向量。实现如下:
def call(self, inputs, training=None):
# 前向计算
# 编码器[b, 784] => [b, z_dim], [b, z_dim]
mu, log_var = self.encoder(inputs)
# 采样reparameterization trick
z = self.reparameterize(mu, log_var)
# 通过解码器生成
x_hat = self.decoder(z)
# 返回生成样本,及其均值与方差
return x_hat, mu, log_var
2. Reparameterization技巧
Reparameterize函数接受均值与方差参数,并从正态分布
N
(
0
,
1
)
\mathcal N(0,1)
N
(
0
,
1
)
中采样获得
ε
ε
ε
,通过
z
=
μ
+
σ
⊙
ε
z=μ+σ \odot ε
z
=
μ
+
σ
⊙
ε
方式返回采样隐向量。代码如下:
def reparameterize(self, mu, log_var):
# reparameterize技巧,从正态分布采样epsilon
eps = tf.random.normal(log_var.shape)
# 计算标准差
std = tf.exp(log_var*0.5)
# reparameterize技巧
z = mu + std * eps
return z
3. 网络训练
网络固定训练100个Epoch,每次从VAE模型中前向计算获得重建样本,通过交叉熵损失函数计算重建误差项
E
z
∼
q
[
log
p
θ
(
x
∣
z
)
]
\mathbb E_{\boldsymbol z\sim q} [\text{log}p_θ (\boldsymbol x|\boldsymbol z)]
E
z
∼
q
[
log
p
θ
(
x
∣
z
)
]
,根据公式
D
K
L
(
q
ϕ
(
z
∣
x
)
∥
p
(
z
)
)
=
−
log
σ
1
+
0.5
σ
1
2
+
0.5
μ
1
2
−
0.5
\mathbb D_{KL} (q_\phi (\boldsymbol z|\boldsymbol x)\|p(\boldsymbol z))=-\text{log}σ_1 +0.5σ_1^2+0.5μ_1^2-0.5
D
K
L
(
q
ϕ
(
z
∣
x
)
∥
p
(
z
)
)
=
−
log
σ
1
+
0
.
5
σ
1
2
+
0
.
5
μ
1
2
−
0
.
5
计算
D
K
L
(
q
ϕ
(
z
∣
x
)
∥
p
(
z
)
)
\mathbb D_{KL} (q_\phi (\boldsymbol z|\boldsymbol x)\|p(\boldsymbol z))
D
K
L
(
q
ϕ
(
z
∣
x
)
∥
p
(
z
)
)
误差项,并自动求导和更新整个网络模型。代码如下:
# 创建网络对象
model = VAE()
model.build(input_shape=(4, 784))
# 优化器
optimizer = tf.optimizers.Adam(lr)
for epoch in range(1000): # 训练100个Epoch
for step, x in enumerate(train_db): # 遍历训练集
# 打平,[b, 28, 28] => [b, 784]
x = tf.reshape(x, [-1, 784])
# 构建梯度记录器
with tf.GradientTape() as tape:
# 前向计算
x_rec_logits, mu, log_var = model(x)
# 重建损失值计算
rec_loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=x, logits=x_rec_logits)
rec_loss = tf.reduce_sum(rec_loss) / x.shape[0]
# 计算KL散度 (mu, var) ~ N (0, 1)
# 公式参考:https://stats.stackexchange.com/questions/7440/kl-divergence-between-two-univariate-gaussians
kl_div = -0.5 * (log_var + 1 - mu**2 - tf.exp(log_var))
kl_div = tf.reduce_sum(kl_div) / x.shape[0]
# 合并误差项
loss = rec_loss + 1. * kl_div
# 自动求导
grads = tape.gradient(loss, model.trainable_variables)
# 自动更新
optimizer.apply_gradients(zip(grads, model.trainable_variables))
if step % 100 == 0:
# 打印训练误差
print(epoch, step, 'kl div:', float(kl_div), 'rec loss:', float(rec_loss))
4. 图片生成
图片生成只利用到解码器网络,首先从先验分布
N
(
0
,
1
)
\mathcal N(0,1)
N
(
0
,
1
)
中采样获得隐向量,再通过解码器获得图片向量,最后Reshape为图片矩阵。例如:
# 测试生成效果,从正态分布随机采样z
z = tf.random.normal((batchsz, z_dim))
logits = model.decoder(z) # 仅通过解码器生成图片
x_hat = tf.sigmoid(logits) # 转换为像素范围
x_hat = tf.reshape(x_hat, [-1, 28, 28]).numpy() *255.
x_hat = x_hat.astype(np.uint8)
save_images(x_hat, 'vae_images/sampled_epoch%d.png' % epoch) # 保存生成图片
# 重建图片,从测试机采样图片
x = next(iter(test_db))
x = tf.reshape(x, [-1, 784]) # 打平
x_hat_logits, _, _ = model(x) # 送入自编码器
x_hat = tf.sigmoid(x_hat_logits) # 将输出转换为像素值
# 输入的前50张+重建的前50张图片合并,[b, 28, 28] => [2b, 28, 28]
x_hat = tf.reshape(x_hat, [-1, 28, 28]).numpy() * 255. # 恢复为0~255范围
x_hat = x_hat.astype(np.uint8)
save_images(x_hat, 'vae_images/rec_epoch%d.png' % epoch) # 保存重建图片
图片重建的效果如下图所示。分别显示了在第1、10、100个Epoch时,输入测试集的图片,获得的重建效果,每张图片的左5列为真实图片,右5列为对应的重建效果。

图片重建:epoch=0

图片重建:epoch=49

图片重建:epoch=99

图片生成:epoch=0

图片生成:epoch=49

图片生成:epoch=99
可以看到,图片重建的效果是要略好于图片生成的,这也说明了图片生成是更为复杂的任务,VAE模型虽然具有图片生成的能力,但是生成的效果仍然不够优秀,人眼还是能够轻松地分辨出及其生成的和真实的图片样本。下一章将要介绍的生成对抗网络在图片生成方面表现更为优秀。
VAE图片生成实战完整代码
import os
import tensorflow as tf
import numpy as np
from tensorflow import keras
from tensorflow.keras import Sequential, layers
from PIL import Image
from matplotlib import pyplot as plt
import ssl
from Chapter12.Fashion_MNIST_dataload import get_data
ssl._create_default_https_context = ssl._create_unverified_context
tf.random.set_seed(22)
np.random.seed(22)
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
assert tf.__version__.startswith('2.')
def save_images(imgs, name):
new_im = Image.new('L', (280, 280))
index = 0
for i in range(0, 280, 28):
for j in range(0, 280, 28):
im = imgs[index]
im = Image.fromarray(im, mode='L')
new_im.paste(im, (i, j))
index += 1
new_im.save(name)
h_dim = 20
batchsz = 512
lr = 1e-3
(x_train, y_train), (x_test, y_test) = get_data()
x_train, x_test = x_train.astype(np.float32) / 255., x_test.astype(np.float32) / 255.
# we do not need label
train_db = tf.data.Dataset.from_tensor_slices(x_train)
train_db = train_db.shuffle(batchsz * 5).batch(batchsz)
test_db = tf.data.Dataset.from_tensor_slices(x_test)
test_db = test_db.batch(batchsz)
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)
z_dim = 10
class VAE(keras.Model):
# 变分自编码器
def __init__(self):
super(VAE, self).__init__()
# Encoder网络
self.fc1 = layers.Dense(128)
self.fc2 = layers.Dense(z_dim) # get mean prediction
self.fc3 = layers.Dense(z_dim)
# Decoder网络
self.fc4 = layers.Dense(128)
self.fc5 = layers.Dense(784)
def encoder(self, x):
# 获得编码器的均值和方差
h = tf.nn.relu(self.fc1(x))
# 获得均值向量
mu = self.fc2(h)
# 获得方差的log向量
log_var = self.fc3(h)
return mu, log_var
def decoder(self, z):
# 根据隐藏变量z生成图片数据
out = tf.nn.relu(self.fc4(z))
out = self.fc5(out)
# 返回图片数据,784向量
return out
def reparameterize(self, mu, log_var):
# reparameterize技巧,从正态分布采样epsilon
eps = tf.random.normal(log_var.shape)
# 计算标准差
std = tf.exp(log_var*0.5)
# reparameterize技巧
z = mu + std * eps
return z
def call(self, inputs, training=None):
# 前向计算
# 编码器[b, 784] => [b, z_dim], [b, z_dim]
mu, log_var = self.encoder(inputs)
# 采样reparameterization trick
z = self.reparameterize(mu, log_var)
# 通过解码器生成
x_hat = self.decoder(z)
# 返回生成样本,及其均值与方差
return x_hat, mu, log_var
# 创建网络对象
model = VAE()
model.build(input_shape=(4, 784))
# 优化器
optimizer = tf.optimizers.Adam(lr)
for epoch in range(100): # 训练100个Epoch
for step, x in enumerate(train_db): # 遍历训练集
# 打平,[b, 28, 28] => [b, 784]
x = tf.reshape(x, [-1, 784])
# 构建梯度记录器
with tf.GradientTape() as tape:
# 前向计算
x_rec_logits, mu, log_var = model(x)
# 重建损失值计算
rec_loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=x, logits=x_rec_logits)
rec_loss = tf.reduce_sum(rec_loss) / x.shape[0]
# 计算KL散度 (mu, var) ~ N (0, 1)
# 公式参考:https://stats.stackexchange.com/questions/7440/kl-divergence-between-two-univariate-gaussians
kl_div = -0.5 * (log_var + 1 - mu**2 - tf.exp(log_var))
kl_div = tf.reduce_sum(kl_div) / x.shape[0]
# 合并误差项
loss = rec_loss + 1. * kl_div
# 自动求导
grads = tape.gradient(loss, model.trainable_variables)
# 自动更新
optimizer.apply_gradients(zip(grads, model.trainable_variables))
if step % 100 == 0:
# 打印训练误差
print(epoch, step, 'kl div:', float(kl_div), 'rec loss:', float(rec_loss))
# evaluation
# 测试生成效果,从正态分布随机采样z
z = tf.random.normal((batchsz, z_dim))
logits = model.decoder(z) # 仅通过解码器生成图片
x_hat = tf.sigmoid(logits) # 转换为像素范围
x_hat = tf.reshape(x_hat, [-1, 28, 28]).numpy() *255.
x_hat = x_hat.astype(np.uint8)
save_images(x_hat, 'Vae_images_sampled02/sampled_epoch%d.png' % epoch) # 保存生成图片
# 重建图片,从测试机采样图片
x = next(iter(test_db))
logits, _, _ = model(tf.reshape(x, [-1, 784])) # 打平并送入自编码器
x_hat = tf.sigmoid(logits) # 将输出转换为像素值
# 恢复为28×28,[b, 784] => [b, 28, 28]
x_hat = tf.reshape(x_hat, [-1, 28, 28])
# 输入的前50张+重建的前50张图片合并,[b, 28, 28] => [2b, 28, 28]
x_concat = tf.concat([x[:50], x_hat[:50]], axis=0)
x_concat = x_concat.numpy() * 255. # 恢复为0~255范围
x_concat = x_concat.astype(np.uint8)
save_images(x_concat, 'Vae_images_rec02/rec_epoch%d.png' % epoch) # 保存重建图片