信号专栏15期。大道至简,心诚则灵!和我们一起轻松学懂信号!
在13期中,我们提到:信号与系统课程的三大变换(傅里叶变换、拉普拉斯变换和z变换)中,傅里叶变换无疑是最为重要的变换,而傅里叶变换的性质又是其中的重点。
连续时间信号傅里叶变换的性质很多,需要掌握的有:对称性(对偶性、互易对称性)、线性、奇偶性(共轭对称性)、展缩特性(尺度变换特性)、时移特性、频移特性以及频域卷积特性等。
每个性质包含三方面的内容:性质本身的数学表示、证明和应用。应用包括在傅里叶变换和反变换计算中的应用,以及理解该性质表达的物理含义。
今天介绍傅里叶变换的时移特性和尺度变换特性一、傅里叶变换的时移特性若已知f(t)的傅里叶变换

那么可知f(t-t0)的傅里叶变换为
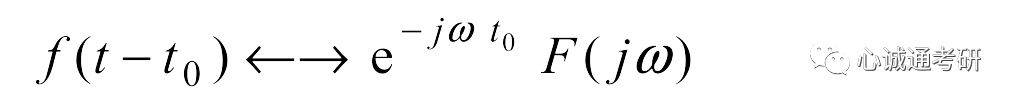
二、该性质的证明

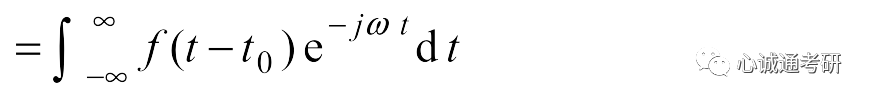
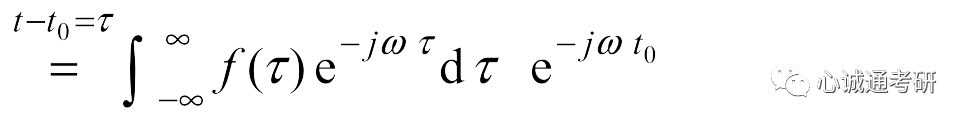
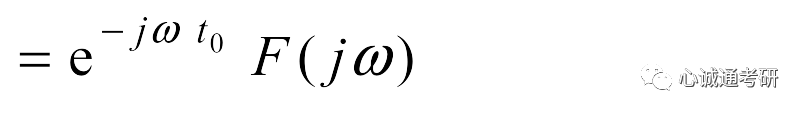
三、傅里叶变换的尺度变换特性若已知f(t)的傅里叶变换

那么f(at)的傅里叶变换为,此处a为非0实数。

四、该性质的证明
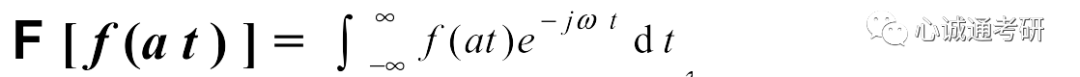
若a>0,则
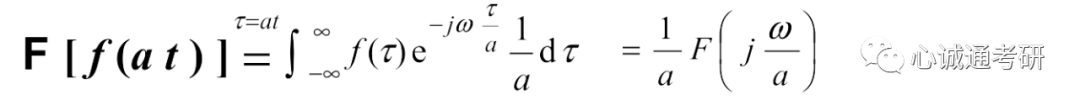
若a<0,则


两种情况可以合并表示为

特别的,当a=-1时
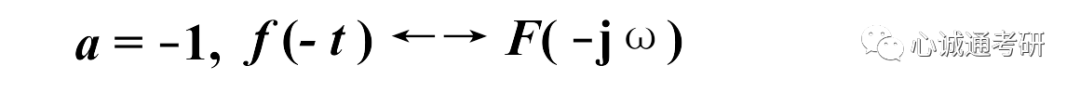
五、应用举例实际中,我们遇到的题目可能是多个性质结合在一起的。下面。举一个线性、时移、尺度变换相结合的例子。例:已知f(t)波形如下图所示,求它的傅里叶变换。
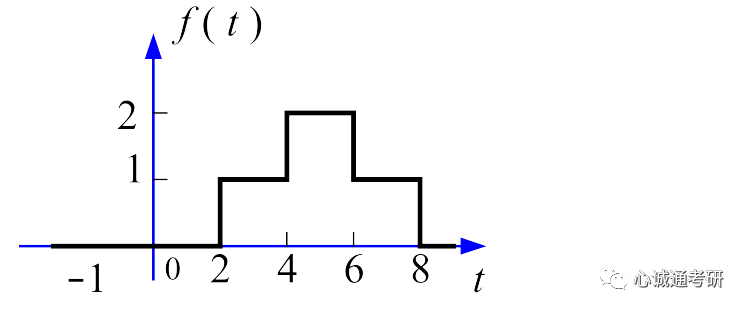
f(t)可以分解为下面两个波形相加f1(t)+f2(t)
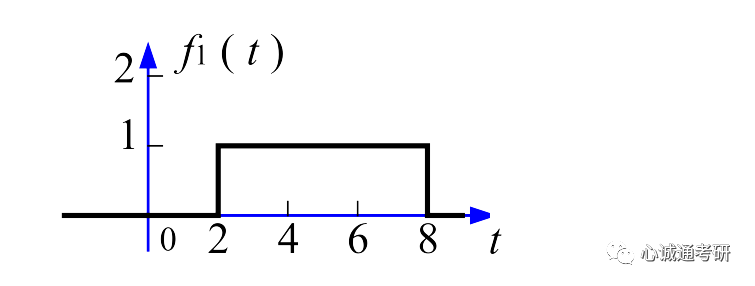
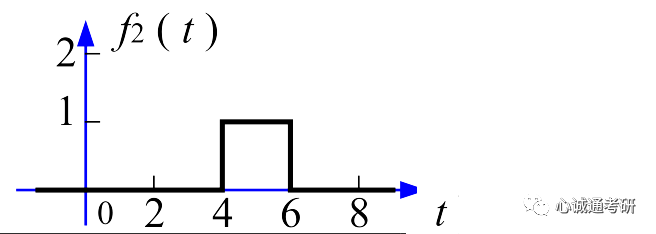
该波形是门函数的时移,可以记作
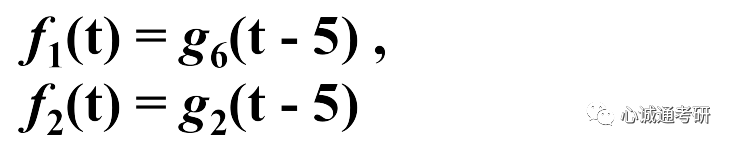
根据时移特性可知
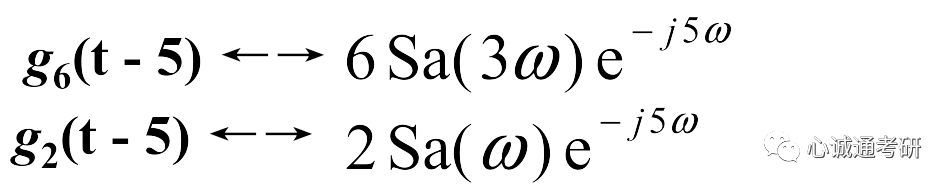
根据线性特性,可以得出
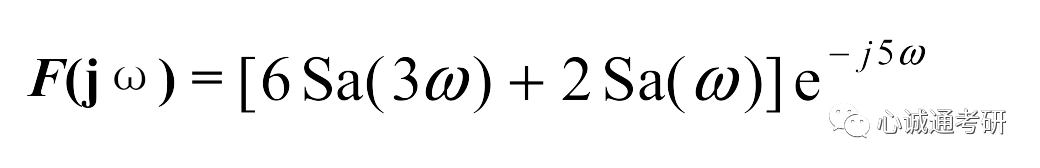
在门函数这一步,也可以通过单位矩形脉冲的傅里叶变换的尺度变换来得到两个函数的傅里叶变换,此处不再详述。
有啥疑问欢迎加qq群:416076455。
点个“
在看
”,祝你成功上岸!