线性时间选择
(一)题目
问题描述
给定线性序集中
n
n
n
个元素和一个正数
k
k
k
,
1
≤
k
≤
n
1\leq k\leq n
1
≤
k
≤
n
,要求找出这
n
n
n
个元素中第
k
k
k
小的元素
注意:
n
n
n
中的元素不重复
(二)解答
1.RandomizedSelect算法
算法思路
在数组
a
[
p
:
r
]
a[p:r]
a
[
p
:
r
]
中随机找一个数
i
i
i
将数组划分成两个子数组
a
[
p
:
i
]
a[p:i]
a
[
p
:
i
]
和
a
[
i
+
1
:
r
]
a[i+1:r]
a
[
i
+
1
:
r
]
,如果数组
a
[
p
:
r
]
a[p:r]
a
[
p
:
r
]
的长度小于等于
k
k
k
,说明第
k
k
k
小的数在这个数组,将其递归,否则递归数组
a
[
i
+
1
:
r
]
a[i+1:r]
a
[
i
+
1
:
r
]
,直到
p
=
r
p=r
p
=
r
,数组被分割成只剩下一个元素,该元素就是第
k
k
k
小的元素。
举例
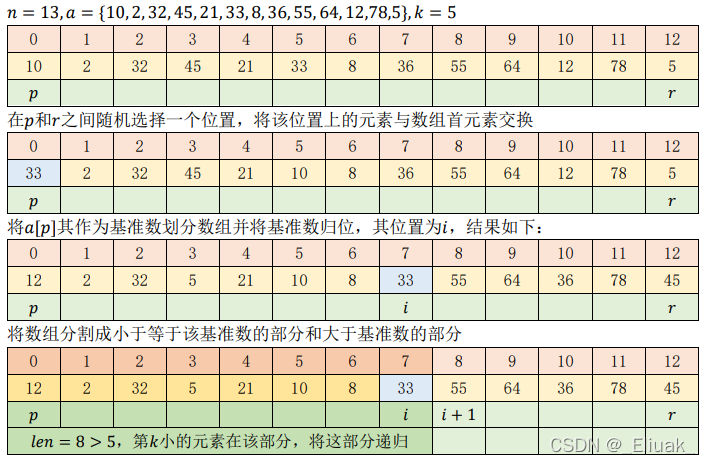
源代码
#include<iostream>
#include<cstdio>
#include<random>
using namespace std;
int n, k, len;
//将数组数组首元素a[p]作为基准数将数组分割
int Partition(int a[], int p, int r);
//交换两个元素
void Swap(int &a, int &b);
//在数组中随机选择一个数将数组分割
int RandomizedPartition(int a[], int p, int r);
//产生随机数
int Random(int x, int y);
//线性划分
int RandomizedSelect(int a[], int p, int r, int k);
int main()
{
//输入数组长度n
cin>>n;
//输入数组
int *a = new int[n];
for (int i = 0; i < n; ++i)
{
cin>>a[i];
}
//输入第k小
cin>>k;
//找第k小并返回
int res = RandomizedSelect(a, 0, n - 1, k);
cout<<res<<endl;
delete []a;
return 0;
}
int Partition(int a[], int p, int r)
{
//i指向首元素,j指向尾元素的下一个元素
int i = p, j = r + 1;
//将首元素作为基准数
int x = a[p];
while (1)
{
//i从基准数右边的元素开始找,直到找到第一个大于等于基准数的元素
while (a[++i] < x && i < r);
//j从尾元素开始找,直到找到第一个小于等于基准数的元素
while (a[--j] > x);
//若i>=j,说明基准数的位置已找到,为j
if (i >= j)
{
break;
}
//交换两个元素,使得基准数左边的数均不大于它,右边的数均不小于它
Swap(a[i], a[j]);
}
//将基准数归位
a[p] = a[j];
a[j] = x;
//返回基准数的位置
return j;
}
void Swap(int &a, int &b)
{
int temp;
temp = a;
a = b;
b = temp;
}
int RandomizedPartition(int a[], int p, int r)
{
//在p和r之间找一个随机数
int i = Random(p, r);
Swap(a[i], a[p]);
return Partition(a, p, r);
}
int Random(int x, int y)
{
return x + rand() % (y - x);
}
int RandomizedSelect(int a[], int p, int r, int k)
{
//数组被分割成只剩下一个元素,该元素就是第k小的元素
if (p == r)
{
return a[p];
}
//在数组中随机找一个数将数组分割,分成小于等于该基准的数组和大于该基准的数组
int i = RandomizedPartition(a, p, r);
//求较小数数组的长度
len = i - p + 1;
//若较小数数组的长度小于等于k,说明第k小的元素在这个数组内,将其递归
if (k <= len)
{
return RandomizedSelect(a, p, i, k);
}
//否则,说明第k小的元素在较大数数组,将其递归
else
{
return RandomizedSelect(a, i + 1, r, k - len);
}
}
2.Select算法
算法思路
将原数组分成
⌈
n
5
⌉
\lceil\frac{n}{5}\rceil
⌈
5
n
⌉
组,每组有5个元素(最后一个数组的元素个数可能不等于5,)将这5个元素排序后找到其中位数并将中位数置于每组的开头,递归调用Select算法找到各组中位数的中位数作为划分基准x(
⌈
n
5
⌉
\lceil\frac{n}{5}\rceil
⌈
5
n
⌉
为奇数时找其中位数,为偶数时找其中位数中较大的那个),划分后的处理与RandomizedSelect算法相同。
举例

源代码
#include<iostream>
#include<cstdio>
#include<random>
using namespace std;
int n, k, len;
//选择排序
void SelectSort(int a[], int p, int r);
//将x作为基准数将数组分割,返回x的位置
int Partition(int a[], int p, int r, int x);
//交换两个元素
void Swap(int &a, int &b);
//找每组的中位数,返回中位数的位置i
int SearchMid(int a[], int p, int r);
//线性划分
int Select(int a[], int p, int r, int k);
int main()
{
//输入数组长度n
cin>>n;
//输入数组
int *a = new int[n];
for (int i = 0; i < n; ++i)
{
cin>>a[i];
}
//输入第k小
cin>>k;
//找第k小并返回
int res = Select(a, 0, n - 1, k);
cout<<res<<endl;
delete []a;
return 0;
}
void SelectSort(int a[], int p, int r)
{
for (int i = p; i < r; ++i)
{
int index = i;
for (int j = i + 1; j <= r; ++j)
{
if (a[j] < a[index])
{
index = j;
}
}
Swap(a[i], a[index]);
}
}
int Partition(int a[], int p, int r, int x)
{
//i指向首元素的前一个位置,j指向尾元素的后一个位置
int i = p - 1, j = r + 1;
while (1)
{
//i从基准数右边的元素开始找,直到找到第一个大于等于基准数的元素
while (a[++i] < x && i < r);
//j从尾元素开始找,直到找到第一个小于等于基准数的元素
while (a[--j] > x && j > p);
//若i>=j,说明基准数的位置已找到,为j
if (i >= j)
{
break;
}
//交换两个元素,使得基准数左边的数均不大于它,右边的数均不小于它
Swap(a[i], a[j]);
}
//返回基准数的位置
return j;
}
void Swap(int &a, int &b)
{
int temp;
temp = a;
a = b;
b = temp;
}
int SearchMid(int a[], int p, int r)
{
//建立与数组a同等大小的数组b
int *b = new int[r - p + 1];
//用数组b存放数组a(注意此时b的首地址为0,而a的首地址为p)
for (int i = p; i <= r; ++i)
{
b[i - p] = a[i];
}
//将数组b排序,b[(r-p+1)/2]为中位数
SelectSort(b, 0, r - p);
for (int i = p; i <= r; ++i)
{
if (a[i] == b[(r - p + 1) / 2])
{
return i;
}
}
delete []b;
return 0;
}
int Select(int a[], int p, int r, int k)
{
if (r - p < 5)
{
SelectSort(a, p, r);
return a[p + k - 1];
}
//分成n/5组,每组5个,找到每组的中位数并将它放到数组首元素的位置
for (int i = 0; i <= (r - p - 4) / 5; ++i)
{
int mid = SearchMid(a, p + 5 * i, p + 5 * i + 4);
Swap(a[mid], a[p + i]);
}
//找到各组中位数的中位数
int x = Select(a, p, p + (r - p - 4) / 5, (r - p - 4) / 10 + 1);
//按照中位数划分
int i = Partition(a, p, r, x);
//求较小数数组的长度
len = i - p + 1;
//若较小数数组的长度小于等于k,说明第k小的元素在这个数组内,将其递归
if (k <= len)
{
return Select(a, p, i, k);
}
//否则,说明第k小的元素在较大数数组,将其递归
else
{
return Select(a, i + 1, r, k - len);
}
}
(三)总结
复杂度分析
1.RandomizedSelect算法
对于RandomizedSelect算法,该算法划分的基准是随机的,最好情况下的时间复杂度为
O
(
n
)
\Omicron(n)
O
(
n
)
,而最坏情况下的时间复杂度为
O
(
n
2
)
\Omicron(n^2)
O
(
n
2
)
,但这种情况在随机划分的过程中发生的的概率极小,因此RandomizedSelect算法的平均时间复杂度为
O
(
n
)
\Omicron(n)
O
(
n
)
。
2.Select算法
对于Select算法,该算法划分的基准是固定的,若能在线性时间内找到一个划分基准,使得按这个基准划分的两个子数组长度均至少为原数组长度的 倍(0<
ε
\varepsilon
ε
<1),那么在最坏情况下,Select算法的时间复杂度也为
O
(
n
)
\Omicron(n)
O
(
n
)
。
例如:当
ε
=
9
10
\varepsilon=\frac{9}{10}
ε
=
1
0
9
时,算法递归调用产生的2个子数组的长度至少缩短
1
10
\frac{1}{10}
1
0
1
。因此,在最坏情况下,算法所需的计算时间
T
(
n
)
T(n)
T
(
n
)
满足
T
(
n
)
≤
T
(
9
n
10
)
+
O
(
n
)
T(n)\leq T(\frac{9n}{10})+\Omicron(n)
T
(
n
)
≤
T
(
1
0
9
n
)
+
O
(
n
)
,解得
T
(
n
)
=
O
(
n
)
T(n)=\Omicron(n)
T
(
n
)
=
O
(
n
)
在线性时间内找到一个划分基准,使得按这个基准划分的两个子数组长度均至少为原数组长度的
ε
\varepsilon
ε
倍(0<
ε
\varepsilon
ε
<1),那么在最坏情况下,Select算法的时间复杂度也为
O
(
n
)
\Omicron(n)
O
(
n
)
。
例如:当
ε
=
9
10
\varepsilon=\frac{9}{10}
ε
=
1
0
9
时,算法递归调用产生的2个子数组的长度至少缩短
1
10
\frac{1}{10}
1
0
1
。因此,在最坏情况下,算法所需的计算时间
T
(
n
)
T(n)
T
(
n
)
满足
T
(
n
)
≤
T
(
9
n
10
)
+
O
(
n
)
T(n)\leq T(\frac{9n}{10})+\Omicron(n)
T
(
n
)
≤
T
(
1
0
9
n
)
+
O
(
n
)
,解得
T
(
n
)
=
O
(
n
)
T(n)=\Omicron(n)
T
(
n
)
=
O
(
n
)