一、无监督学习

无监督学习是机器学习算法中的一种。监督学习的目的主要是对数据进行分类和回归预测，它主要是通过已知推测未知，大部分监督学习算法有一个训练模型的过程；相对于监督学习，无监督学习则是主要着重于数据的分布特点，与有监督学习不同，无监督学习并没有训练的过程。

二、聚类

针对给定的样本数据，聚类算法会根据它们的特征相似度或距离，把相似的数据划分为若干个簇中。相似的样本划分到相同的簇中，不相似的样本划分到不同的簇。聚类处理数据的过程也是从未知到已知的过程，因为聚类算法在事先并不知道聚类得到的簇的特点和样本的分布。

k-means属于无监督学习中聚类算法的一种。

三、 k均值聚类算法

3.1 k-means

k均值聚类算法将样本集划分为k个簇，把每个样本数据划分到距离最近的簇中，且每个样本仅属于一个类，此为k均值聚类算法。k-mean算法属于硬聚类，即每个样本只能属于一个簇。

聚合聚类需要预先考虑以下几个要素：

距离或相似度；
合并规则；
停止条件。

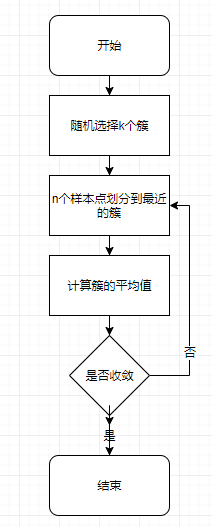
3.2 步骤

随机选择k个簇作为

质心

（需要保证这k个簇的特征值在样本集特征值的范围之内）；
把n个样本点划分到距离最近的簇中；
计算每个簇的平均值。
判断是否收敛，如果没有收敛，则从步骤2开始。

通过图2可以了解到，由于第三张图和第四张图未发生变化，则表示此时的簇已经收敛。

3.3 实现

from numpy import *
from matplotlib import pyplot as plt
import matplotlib


def load_data_set(filename):
    data_matrix = []
    with open(filename) as fp:
        for line in fp.readlines():
            # 多个浮点型的列
            data = line.strip().split('\t')
            float_data = [float(datum) for datum in data]
            data_matrix.append(float_data)
    return data_matrix

load_data_set函数用于将文本文件导入成一个列表中。

def euclidean_distance(vec_a, vec_b):
    """计算两个向量的欧式距离"""
    return sqrt(sum(power(vec_a - vec_b, 2)))

距离的计算有很多种选择，比如闵可夫斯基距离、马氏距离等，不同的距离选择会使得计算页会有所不同。这里选择的是欧氏距离，即各个特征差值的平方再开方（勾股定理的计算就用到了欧式距离），

马氏距离是欧式距离的推广

。

def random_centroids(data_set, k):
    """
    返回k个随机的质心 保证这些质心随机并且不超过整个数据集的边界
    :param data_set: 数据集
    :param k: 质心的数量
    :return: k个随机的质心
    """
    # 创建一个k行n列的矩阵，用于保存随机质心
    n = shape(data_set)[1]
    centroids = mat(zeros((k, n)))
    # 对n个特征进行遍历
    for j in range(n):
        minJ = min(data_set[:, j])
        rangeJ = float(max(data_set[:, j]) - minJ)
        centroids[:, j] = minJ + rangeJ * random.rand(k, 1)
    return centroids

random_centroids的作用就是随机创建k个质心。data_set[:, j]获取的是第j列的所有元素，这种用法是numpy对

__getitem__()

即切片方法的重写。

def kMeans(data_set, k, distance_measure=euclidean_distance, create_centroids=random_centroids):
    """
    k means 算法
    :param data_set: 数据集
    :param k: k means算法的k 即要生成几个簇
    :param distance_measure: 计算距离函数
    :param create_centroids: 创建质心的函数
    :return:
    """
    m = shape(data_set)[0]
    # 向量分配到某一个(簇索引值,误差)
    cluster_assment = mat(zeros((m, 2)))
    # 创建k个质心
    centroids = create_centroids(data_set, k)
    cluster_changed = True

    while cluster_changed:
        cluster_changed = False
        # 计算该点离哪个质心最近
        for i in range(m):
            min_index, min_dist = -1, inf
            # 遍历k个质心 获取一个最近的质心
            for j in range(k):
                # 计算该点和质心j的距离
                distJI = distance_measure(centroids[j, :], data_set[i, :])
                if distJI < min_dist:
                    min_dist, min_index = distJI, j
            # 分配质心索引发生了变化 则仍然需要迭代
            if cluster_assment[i, 0] != min_index:
                cluster_changed = True
            # 不断更新最小值
            cluster_assment[i, :] = min_index, min_dist ** 2
        print(centroids)
        # 更新质心
        for cent in range(k):
            # 获取属于该簇的所有点
            ptsInClust = data_set[nonzero(cluster_assment[:, 0].A==cent)[0]]
            # 按矩阵的列进行均值计算
            centroids[cent, :] = mean(ptsInClust, axis=0)
        # 显示每一次迭代后的簇的情况
        # show_image(data_set, centroids, cluster_assment)
    return centroids, cluster_assment

kMeans函数就是之前流程图的实现，它会迭代到簇收敛为止。

def show_image(data_set, centroids, clustAssing):
    colors = 'bgrcmykb'
    markers = 'osDv^p*+'
    for index in range(len(clustAssing)):
        datum = data_set[index]
        j = int(clustAssing[index, 0])
        flag = markers[j] + colors[j]
        plt.plot(datum[:, 0], datum[:, 1], flag)
    # 质心
    plt.plot(centroids[:, 0], centroids[:, 1], '+k')

show_image函数用于点的分类的显示，它目前最多显示4个簇，过多的时候需要再sign和color上添加；除此之外，这个函数目前只能显示两个特征值，当有多个特征值的时候，可以考虑进行降维处理。

接着是主函数和数据：

if __name__ == '__main__':
    data_mat = mat(load_data_set('testSet.txt'))
    centroids, clustAssing = kMeans(data_mat, 4)
    print('----')
    # print(clustAssing)
    show_image(data_mat, centroids, clustAssing)
    plt.show()

数据集：

dataSet.txt

把上述数据保存为dataSet.txt和之前的kMeans.py放入同一文件夹下运行即可得到图 2所示的收敛图。

3.4 sklearn实现

python有着完整的机器学习的库，通过调用这些库，可以在很大程度上减少代码的编写和错误率。

"""
使用sklearn提供的K均值聚类算法
"""
import numpy
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

from kMeans import load_data_set


def show_image(data_set, centroids, cluster_centers):
    colors = 'bgrcmykb'
    markers = 'osDv^p*+'
    for index in range(len(cluster_centers)):
        datum = data_set[index]
        j = int(cluster_centers[index])
        flag = markers[j] + colors[j]
        plt.plot(datum[:, 0], datum[:, 1], flag)
    # 质心
    plt.plot(centroids[:, 0], centroids[:, 1], '+k')


if __name__ == '__main__':
    data_set = numpy.mat(load_data_set('testSet.txt'))
    kmeans_model = KMeans(n_clusters=4).fit(data_set)
    # 显示模型
    show_image(data_set, kmeans_model.cluster_centers_, kmeans_model.labels_)
    plt.show()

运行结果如下：

四、二分K-均值算法

把数据集切换为

dataSet2.txt

后，再次运行之前的kMeans算法可能会得到下图的结果：

k均值聚类算法能够保证收敛局部最优性，它的聚类效果在很大程度上依赖于随机质心的选择，这会造成算法收敛但聚类效果却较为一般。二分K-均值算法可以避免此类问题。

一种用于度量聚类效果的指标是SSE(Sum of Square Error, 误差平方和)，它等于所有的样本点到对应的簇的距离的平方的和，也就是上面的kMeans函数内部cluster_assment的第一列的和（用代码实现就是sum(cluster_assment[:, 1])）。SSE越小表示数据点越接近于它们的质心，聚类效果也就越好。

4.1 思路

该算法首先将所有的样本点作为一个簇，然后将该簇一分为二；之后选择其中一个可以在最大程度上降低SSE值的簇进行划分，直到满足停止条件为止。这里的停止条件是划分的簇的数量达到了k后则停止划分。

把所有的点作为一个簇；
判断当前簇的数量是否大于等于k，如果是则直接退出，否则向下执行；
对于每一个簇，在给定的簇上进行K-均值聚类（k=2），并计算将该簇一分为二之后的总误差；
选择使得误差最小的那个簇进行划分操作；跳转到步骤2。

4.2 代码实现

def binary_kmeans(data_set, k, distance_measure=euclidean_distance):
    """
    二分 K-均值算法
    :param data_set: 样本集
    :param k: 要划分的簇的数量
    :param distance_measure: 距离计算函数
    :return: 返回同kMeans()函数
    """
    m = shape(data_set)[0]
    cluster_assment = mat(zeros((m, 2)))
    # 按照列求平均数并转换成列表
    centroid0 = mean(data_set, axis=0).tolist()[0]
    # 划分的簇
    cent_list = [centroid0]
    # 计算点当前簇的误差
    for j in range(m):
        cluster_assment[j, 1] = distance_measure(mat(centroid0), data_set[j, :]) ** 2
    # 划分的簇小于选定值时 继续划分
    while len(cent_list) < k:
        lowestSSE = inf
        # 找到一个划分后SSE最小的簇
        for i in range(len(cent_list)):
            # 获取该簇的所有数据
            ptsInCurrCluster = data_set[nonzero(cluster_assment[:, 0].A == i)[0], :]
            # 经过划分 一个簇得到编号分别为0和1的两个簇
            centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distance_measure)
            # 计算分簇之后的Sum of Square Error
            sseSplit = sum(splitClustAss[:, 1])
            sseNotSplit = sum(cluster_assment[nonzero(cluster_assment[:, 0].A != i)[0], 1])

            print('sseSplit, and not split', sseSplit, sseNotSplit)
            if sseSplit + sseNotSplit < lowestSSE:
                bestCentToSplit = i
                bestNewCents = centroidMat
                bestClustAss = splitClustAss.copy()
                lowestSSE = sseSplit + sseNotSplit
        # 重新编排编号
        bestClustAss[nonzero(bestClustAss[:, 0].A == 1)[0], 0] = len(cent_list)
        bestClustAss[nonzero(bestClustAss[:, 0].A == 0)[0], 0] = bestCentToSplit

        print('the bestCentToSplit is:', bestCentToSplit)
        print('the len of bestClustAss is', len(bestClustAss))
        cent_list[bestCentToSplit] = bestNewCents.tolist()[0]
        cent_list.append(bestNewCents.tolist()[1])
        cluster_assment[nonzero(cluster_assment[:, 0].A == bestCentToSplit)[0], :] = bestClustAss
        # 显示每一次迭代后的簇的情况
        show_image(data_set, mat(cent_list), cluster_assment)

    return mat(cent_list), cluster_assment

在二分K-均值算法中主要有两个循环，第一重循环用于确定簇的个数，第二重循环用于选定一个能使得SSE降到最低的划分。在划分完成后，一个簇被划分成了两个簇，需要对这个簇进行一些后续的操作：编排序号（序号是由k均值聚类算法给定的）和添加到簇列表中。

二分K-均值算法可以很好地解决k均值聚类算法的问题，不过目前的k值仍然需要预先给定。

参考：

《机器学习实战》
《统计学习方法》
《Python 机器学习及实践》

原文链接：https://blog.csdn.net/bull521/article/details/102455047