写在最前面的话
快说谢谢学姐!!!
注意:本博客仅供参考!!!
作业一
1
考虑一个实时的在线电话翻译系统,该系统实现英语与日语之间的实时在线翻译,讨论该系统的性能度量,环境,执行器,感知器,并对该环境的属性进行分析。
性能度量:翻译的正确率
环境:电话线路
传感器:麦克风
执行器:音响
完全可观察的,单agent,确定的(无噪音条件下),片段的,静态的,离散的。
2
考虑一个医疗诊断系统的Agent,讨论该Agent最合适的种类(简单Agent,基于模型的Agent,基于目标的Agent和基于效用的Agent)并解释你的结论。
utility-based agent 基于效用的Agent
能够治愈病人的方法有很多种,系统必须衡量最优的方法来推荐给病人
3
先建立一个完整的搜索树,起点是S,终点是G,如下图,节点旁的数字表示到达目标状态的距离,然后用以下方法表示如何进行搜索,并分析几种算法的完备性、最优性、以及时间复杂度和空间复杂度。 a.深度优先; b.广度优先; c.爬山法; d.最佳优先;
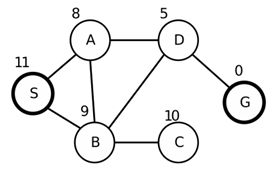

深度优先搜索:在有限状态空间中,深度优先搜索是完备的,因为它至多扩展所有结点,但在树搜索中,则不完备(因为算法可能会陷入死循环);该算法无法避免冗余路径,因此不是最优的;深度优先搜索只需要存储O(bm)个结点,因此空间复杂度为O(bm);该算法可能搜索树上每个结点,因此时间复杂度为O(b^m)。(其中b为分支因子,m为树的最大深度)
广度优先搜索:首先,广度优先搜索是完备的(如果最浅的目标结点处于一个有限深度d,广度优先搜索在扩展完比它浅的所有结点之后最终一定能找到该目标结点;其次,如果路径代价是基于结点深度的非递减函数,则广度优先搜索是最优的;该方法的时间复杂度为O(b^d)(假设解的深度为d);该方法的空间复杂度同样为O(b^d)(因为有O(b^d)个结点在边缘结点中。
爬山法:
考虑随机重启时,全程遍历,时间与空间复杂度可以为O(b^d)
(1)利用最陡爬山法
最陡爬山法是一个简单的循环过程,不断地向值增加的方向持续移动,这里选择的就是距离最小的值移动。爬山算法,是一种局部贪心的最优算法. 该算法的主要思想是:每次拿相邻点与当前点进行比对,取两者中较优者,作为爬坡的下一步。在S点出发,因为h(A)=8,小于h(B),所以爬山爬到A,之后类似这样就到D,最后到G。路径就是S-A-D-G.
最陡爬山法不具有完备性,因为会经常陷入困境,不一定能找到解。而且只能找到多个局部最优点的其中一个,不一定是全局最优点,所以不具有最优性。因为从上到下,每层只生成和保存一个结点,所以时间复杂度和空间复杂度都是O(d)。d为目标结点或者局部最优结点的深度。
(2)首选爬山法
依次寻找该点X的邻近点中首次出现的比点X价值高的点,并将该点作为爬山的点。依次循环,直至该点的邻近点中不再有比其大的点.
利用首选爬山法可能得到以上3条可能的路径,分别用不同颜色标注。
在S的时候,随机生成A,因为A比当前较优,所以从A再随机生成下一个结点,因为B=9,比当前差,放弃再生成D,最后得到S->A->D->G这条路径。另外两条也是根据这个方法推出。
首选爬山法不具有最优性和完备性。因为从上到下,每层只生成和保存一个结点,所以时间复杂度和空间复杂度都是O(d)。d为目标结点或者局部最优结点的深度
最佳优先搜索:
完备性:贪婪最佳优先搜索是不完备的(有限状态空间的图索索版本是完备的)。A* 搜索是完备的。
最优性:贪婪最优先佳搜索:每次扩展是局部最优的选择,可能不能达到全局最优,所以 不是最优的。A*搜索:如果h(n)是可采纳的,则树搜索版本是 最优的。如果h(n)是⼀致的,则图搜索版本是 最优的。
时间复杂度:
贪婪最佳优先搜索:与深度优先类似,时间复杂度为O(b^m)。
A* 搜索:O(b^d),其中 d=h*-h, 为到⽬标结点的实际代价。
空间复杂度:
贪婪最佳优先搜索:O(b^m)。
A* 搜索:O(b^d),其中 d=h*-h。
4
图二是一棵部分展开的搜索树,其中树的边记录了对应的单步代价,叶子节点标注了到达目标结点的启发式函数的代价值,假定当前状态位于结点A。
a) 用下列的搜索方法来计算下一步需要展开的叶子节点。注意必须要有完整的计算过程,同时必须对扩展该叶子节点之前的节点顺序进行记录:
1.贪婪最佳优先搜索
2. 一致代价搜索
3. A*树搜索
(b) 讨论以上三种算法的完备性和最优性。
a)
贪婪最佳优先:如果h(B)>5,首先访问叶子结点C,如果h(B)<=5,首先访问B,再访问C
一致代价搜索:B,D,E,F,G,H,C
A*树搜索:如果h(B)>15,首先访问D;如果h(B)<=15,首先访问B,再E,G,D,H,F,C
b)
贪婪最佳优先搜索:该方法不能保证找到解,因此是不完备的;该方法不一定能找到最优解,因此不是最优的。
一致代价搜索:该方法在存在零代价行动时可能陷入死循环,因此是不完备的,如果每一步的代价都大于等于某个小的正值常数ε,那么一致搜索是完备的;一致代价搜索按照结点的最优路径扩展结点,因此是最优的。
A*树搜索:该方法能保证找到解,因此是完备的;因为h(n)是可采纳的,因此A*树搜索是最优的。
5
给定一个启发式函数满足h(G)=0,其中G是目标状态,证明如果h是一致的,那么它是可采纳的。
假设n为任意一个状态,G是任意一个目标状态。n,n1,n2,....,nm,G为从状态n到达状态G的一条最优路径,我们已知
评估代价f(n)=g(n)+h(n)
真实代价 f’(n)=g(n)+c(n,a1,n1)+c(n1,a2,n2)+….c(nm,am+1,G)
目标:证明 f(n)<=f’(n)
证明:
f(n)=g(n)+h(n)
<=g(n)+c(n,a1,n1)+h(n1)
<= g(n)+c(n,a1,n1)+c(n1,a2,n2)+h(n2)
<=...
<=g(n)+c(n,a1,n1)+c(n1,a2,n2)+….c(nm,am+1,G)+h(G)=f’(n)
作业二
1
请用真值表的方法证明下列语句是有效的,可满足的,还是不可满足的?
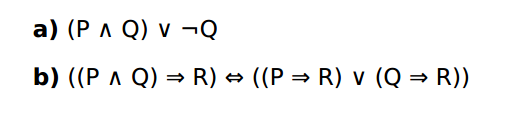

2
考虑下列的一阶逻辑表达式:

其中x,y,z,w,s,t是变量,a,b,c是常数。
a)讲1,2,3式子转换为CNF形式
b)从上述知识库(KB)中使用归结算法证明结论equal(c,a)。

3
把下列表达式转换为CNF形式
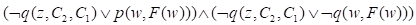

4
考虑从一副标准的52张纸牌(不含大小王)中分发每手5张牌的扑克牌域。假设发牌人是公平的。
a)在联合概率分布中共有多少个原子事件(即,共有多少种5张手牌的组合)?
b)每个原子事件的概率是多少?
c)拿到大同花顺(即同花的A、K、Q、J、10)的概率是多少?
d)四同张(4张相同的牌,分别为4种花色)的概率是多少?

5
参考下图中的贝叶斯网络,其中布尔变量I=聪明(intelligence) H=诚实(Honest) P=受欢迎的(Popular) L=大量的竞选资金 E=竞选成功

a.根据该网络结构,是否可以得到P(I,L,H)=P(I)P(L)P(H),如果不是,请给出正确的表达式;
b.根据该网络结构计算P(i,h,¬l,p,¬e)的值,只有答案没有步骤不得分;
c.假设已知某个人是诚实的,没有大量的竞选资金但是竞选成功了,那么他是聪明的概率是多少?只有答案没有过程不得分。
(a)
P(I,L,H)=P(I)P(L|H)P(H)
(b)
P(i, h, ¬l, p, ¬e)=P(¬e|p)P(p|i, h,¬l)P(i)P(¬l|h)P(h)=0.0056
(c)
P(i, h, ¬l, p, e)=P(i)P(h)P(¬l|h)P(p|i, h, ¬l)P(e|p)=0.0084
P(i, h, ¬l, ¬p, e)=P(i)P(h)P(¬l|h)P(¬p|i, h, ¬l)P(e|¬p)=0.0021
P(¬i, h, ¬l, p, e)=0.0063
P(¬i, h, ¬l, ¬p, e)=0.00245
P(i|h, e, ¬l)=P(i, h, e, ¬l)/P(h, e, ¬l)=( P(i, h, ¬l, p, e)+ P(i, h, ¬l, ¬p, e))/( P(i, h, ¬ l, p, e)+ P(i, h, ¬l, ¬p, e)+ P(¬i, h, ¬l, p, e)+ P(¬i, h, ¬l, ¬p, e))=0.5455
这道题我要吐槽一下,我实在是没有想到我居然抄数字抄错了,然后就导致了我的答案后面全算错了。老师当时对抄袭行为看得很重,结果一个朋友就抄的我的,然后那时候就特别担心被抓抄袭。结果助教批改的时候给我扣了分,给朋友是全对,我麻了。
作业三
1
贝叶斯网络
根据图所给出的贝叶斯网络,其中:P(A)=0.5,P(B|A)=1, P(B|¬A)=0.5, P(C|A)=1, P(C|¬A)=0.5,P(D|BC)=1,P(D|B, ¬C)=0.5,P(D|¬B,C)=0.5,P(D|¬B, ¬C)=0。试计算下列概率P(A|D)。
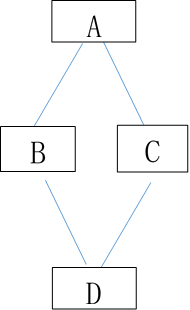

2
概率推理
设有如下推理规则
r1: IF E1 THEN (2, 0.00001) H1
r2: IF E2 THEN (100, 0.0001) H1
r3: IF E3 THEN (200, 0.001) H2
r4: IF H1 THEN (50, 0.1) H2
且已知P(E1)= P(E2)= P(H3)=0.6, P(H1)=0.091, P(H2)=0.01, 又由用户告知:
P(E1| S1)=0.84, P(E2|S2)=0.68, P(E3|S3)=0.36
请用主观Bayes方法求P(H2|S1, S2, S3)=?
(1) 由r1计算O(H1| S1)
(2) 由r2计算O(H1| S2)(3) 计算O(H2| S1,S2,S3)和P(H2| S1,S2,S3)
(3) 计算O(H1| S1,S2)和P(H1| S1,S2)
(4) 由r3计算O(H2| S3)
(5) 由r4计算O(H2| H1)
(6) 计算O(H2| S1,S2,S3)和P(H2| S1,S2,S3)
(1) 先把H1的先验概率更新为在E1下的后验概率P(H1| E1)
P(H1| E1)=(LS1 × P(H1)) / ((LS1-1) × P(H1)+1)
=(2 × 0.091) / ((2 -1) × 0.091 +1)
=0.16682
由于P(E1|S1)=0.84 > P(E1),使用P(H | S)公式的后半部分,得到在当前观察S1下的后验概率P(H1| S1)和后验几率O(H1| S1)
P(H1| S1) = P(H1) + ((P(H1| E1) – P(H1)) / (1 - P(E1))) × (P(E1| S1) – P(E1))
= 0.091 + (0.16682 –0.091) / (1 – 0.6)) × (0.84 – 0.6)
=0.091 + 0.18955 × 0.24 = 0.136492
O(H1| S1) = P(H1| S1) / (1 - P(H1| S1))
= 0.15807
(2) 由r2计算O(H1| S2)
先把H1的先验概率更新为在E2下的后验概率P(H1| E2)
P(H1| E2)=(LS2 × P(H1)) / ((LS2-1) × P(H1)+1)
=(100 × 0.091) / ((100 -1) × 0.091 +1)
=0.90918
由于P(E2|S2)=0.68 > P(E2),使用P(H | S)公式的后半部分,得到在当前观察S2下的后验概率P(H1| S2)和后验几率O(H1| S2)
P(H1| S2) = P(H1) + ((P(H1| E2) – P(H1)) / (1 - P(E2))) × (P(E2| S2) – P(E2))
= 0.091 + (0.90918 –0.091) / (1 – 0.6)) × (0.68 – 0.6)
=0.25464
O(H1| S2) = P(H1| S2) / (1 - P(H1| S2))
=0.34163
(3) 计算O(H1| S1,S2)和P(H1| S1,S2)
先将H1的先验概率转换为先验几率
O(H1) = P(H1) / (1 - P(H1)) = 0.091/(1-0.091)=0.10011
再根据合成公式计算H1的后验几率
O(H1| S1,S2)= (O(H1| S1) / O(H1)) × (O(H1| S2) / O(H1)) × O(H1)
= (0.15807 / 0.10011) × (0.34163) / 0.10011) × 0.10011
= 0.53942
再将该后验几率转换为后验概率
P(H1| S1,S2) = O(H1| S1,S2) / (1+ O(H1| S1,S2))
= 0.35040
(4) 由r3计算O(H2| S3)
先把H2的先验概率更新为在E3下的后验概率P(H2| E3)
P(H2| E3)=(LS3 × P(H2)) / ((LS3-1) × P(H2)+1)
=(200 × 0.01) / ((200 -1) × 0.01 +1)
=0.09569
由于P(E3|S3)=0.36 < P(E3),使用P(H | S)公式的前半部分,得到在当前观察S3下的后验概率P(H2| S3)和后验几率O(H2| S3)
P(H2| S3) = P(H2 | ¬ E3) + (P(H2) – P(H2| ¬E3)) / P(E3)) × P(E3| S3)
由当E3肯定不存在时有
P(H2 | ¬ E3) = LN3 × P(H2) / ((LN3-1) × P(H2) +1)
= 0.001 × 0.01 / ((0.001 - 1) × 0.01 + 1)
= 0.00001
因此有
P(H2| S3) = P(H2 | ¬ E3) + (P(H2) – P(H2| ¬E3)) / P(E3)) × P(E3| S3)
=0.00001+((0.01-0.00001) / 0.6) × 0.36
=0.00600
O(H2| S3) = P(H2| S3) / (1 - P(H2| S3))
=0.00604
(5) 由r4计算O(H2| H1)
先把H2的先验概率更新为在H1下的后验概率P(H2| H1)
P(H2| H1)=(LS4 × P(H2)) / ((LS4-1) × P(H2)+1)
=(50 × 0.01) / ((50 -1) × 0.01 +1)
=0.33557
由于P(H1| S1,S2)=0.35040 > P(H1),使用P(H | S)公式的后半部分,得到在当前观察S1,S2下H2的后验概率P(H2| S1,S2)和后验几率O(H2| S1,S2)
P(H2| S1,S2) = P(H2) + ((P(H2| H1) – P(H2)) / (1 - P(H1))) × (P(H1| S1,S2) – P(H1))
= 0.01 + (0.33557 –0.01) / (1 – 0.091)) × (0.35040 – 0.091)
=0.10291
O(H2| S1,S2) = P(H2| S1, S2) / (1 - P(H2| S1, S2))
=0.10291/ (1 - 0.10291) = 0.11472
(6) 计算O(H2| S1,S2,S3)和P(H2| S1,S2,S3)
先将H2的先验概率转换为先验几率
O(H2) = P(H2) / (1 - P(H2) )= 0.01 / (1-0.01)=0.01010
再根据合成公式计算H1的后验几率
O(H2| S1,S2,S3)= (O(H2| S1,S2) / O(H2)) × (O(H2| S3) / O(H2)) ×O(H2)
= (0.11472 / 0.01010) × (0.00604) / 0.01010) × 0.01010
=0.06832
再将该后验几率转换为后验概率
P(H2| S1,S2,S3) = O(H1| S1,S2,S3) / (1+ O(H1| S1,S2,S3))
= 0.06832 / (1+ 0.06832) = 0.06395
可见,H2原来的概率是0.01,经过上述推理后得到的后验概率是0.06395,它相当于先验概率的6倍多。
3
极大后验概率
某学校,所有的男生都穿裤子,而女生当中,一半穿裤子,一半穿裙子。男女比例70%的可能性是4:6,有20%可能性是1:1,有10%可能性是6:4,问一个穿裤子的人是男生的概率有多大?
(1)假设情况h1,其发生概率P(h1) = 7/10,此时男女比例4:6,则 P(pants):P(skirt) =7:3
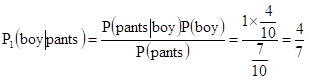
(2)假设情况h2,其发生概率P(h2) = 2/10,此时男女比例1:1,则 P(pants):P(skirt) = 3:1
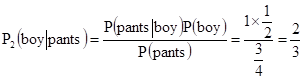
(3)假设情况h3,其发生概率P(h3) = 1/10,此时男女比例6:4,则 P(pants):P(skirt) = 8:2
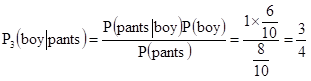
由MAP可得:

极大后验概率其实就是选择概率最大的那个当作结果
4
设样本集合如下表格,其中A、B、C是F的属性,请根据信息增益标准(ID3算法),画出F的决策树。其中
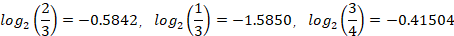


所以,第一次分类选择属性C,对C=0的4个例子再进行第二次分类:

所以,可任选属性A或B作为第二次分类的标准,在这里选择属性A,则A=1的两个例子再按照属性B分类,得:
F的决策树:

5
人工神经网络
阈值感知器可以用来执行很多逻辑函数,说明它对二进制逻辑函数与(AND)和或(OR)的实现过程。
与(AND)操作的真值表如下表所示:

与操作可用下图所示的阈值感知器表示:

v = w1x1+w2x2+b = x1+x2 -1.5
If x1=x2=1 , then v = 0.5, and y=1
If x1 = 0,and x2=1 , then v= -0.5 , and y=0
If x1 = 1,and x2=0 , then v= -0.5 , and y=0
If x1=x2=0, then v= -1.5 , and y=0
或(OR)操作的真值表如下所示:

或操作可用下图所示的阈值感知器表示:

学姐辛苦啦~