SPSS(十六)SPSS之判别分析(图文+数据集)
判别分析又称“分辨法”,是在分类确定的条件下,根据某一研究对象的各种特征值判别其类型归属问题的一种多变量统计分析方法。
聚类分析与判别分析的区别与联系
都是研究分类的,在进行聚类分析前,对总体到底有几种类型不知道(研究分几类较为合适需从计算中加以调整)。判别分析则是在总体类型划分已知,对当前新样本判断它们属于哪个总体。如我们对研究的多元数据的特征不熟悉,当然要进行聚类分析,才能考虑判别分析问题。
判别分析概述
判别分析的一般形式:y=a1x1+a2x2+……+anxn
非常明确共有几个类别
目的是从已知样本中训练出判别函数
用途
对客户进行信用预测
寻找潜在客户
判别分析
常用判别
方法
-
最大似然法
用于自变量均为分类变量的情况
计算出这些情况的概率组合,基于这些组合大小进行判别
- 距离判别
对新样品求出他们离各个类别重心的距离远近
适用于自变量均为连续变量的情况,对变量分布类型无严格要求
-
Fisher判别法
与主成份分析有关
对分布、方差等都没有什么限制
按照类别与类别差异最大原则提取公因子然后使用公因子判别
- Bayes判别
计算该样品落入各个子域的概率
强项是进行多类判别
要求总体呈多元正态分布
利用贝叶斯公式,概率分布逻辑衍生出来一个判别方法,计算这个样本落入这个类别的概率,概率最大就被归为一类
判别分析适用条件(有点类似多重回归分析)
- 各自变量为连续性或有序分类变量
- 样本来自一个多元正态总体,该前提几乎做不到
- 各组的协方差矩阵相等,类似与方差分析中的方差齐
- 变量间独立,无共线性
-
违反条件影响也不大,主要看预测准不准,准的话违反也无所谓
判别函数
效果的验证
方法
利用判别分析得出判别函数,那我们怎么其效果好不好?
-
自身验证
(拿训练数据直接预测验证,但是对预测样本预测好不代表对新样本预测好) -
外部数据验证(收集新的数据来验证,这是最客观最有效的,但是麻烦而且两次收集的数据不一定是同质的)
-
样本二分法(一般划分2/3为训练集,1/3为验证集,但是浪费了1/3的样本)
-
交互验证(Cross-Validation)—-
刀切法(10分法,数据划分为10个集合,每次挑选一个出来做验证集,其余9个做训练集,可以做10次,因为验证集可换10种可能)
案例:
鸢尾花数据(
Fisher判别法)
Fisher在研究有关判别分析方法的时候所使用的资料,包含了刚毛、变色、弗吉尼亚这三种鸢尾花的花萼长、宽和花瓣长、宽,分析目的是希望能够使用这4个变量来对花的种类进行区分。
数据集如下
1 1 50 33 14 2
2 3 67 31 56 24
3 3 89 31 51 23
4 1 46 36 10 2
5 3 65 30 52 20
6 3 58 27 51 19
7 2 57 28 45 13
8 2 63 33 47 16
9 3 49 25 45 17
10 2 70 32 47 14
11 1 48 31 16 2
12 3 63 25 50 19
13 1 49 36 14 1
14 1 44 32 13 2
15 2 58 26 40 12
16 3 63 27 49 18
17 2 50 23 33 10
18 1 51 38 16 2
19 1 50 30 16 2
20 3 64 28 56 21
21 1 51 38 19 4
22 1 49 30 14 2
23 2 58 27 41 10
24 2 60 29 45 15
25 1 50 36 14 2
26 3 58 37 51 19
27 3 64 28 56 22
28 3 63 28 51 15
29 2 62 22 45 15
30 2 61 30 46 14
31 2 56 25 39 11
32 3 68 32 59 23
33 3 62 34 54 23
34 3 67 33 57 25
35 1 55 35 13 2
36 2 64 32 45 15
37 3 59 30 51 18
38 3 64 32 53 23
39 2 54 30 45 15
40 3 67 33 57 21
41 1 44 30 13 2
42 1 47 32 16 2
43 3 72 32 60 18
44 3 61 30 49 18
45 1 50 32 12 2
46 1 43 30 11 1
47 2 67 31 44 14
48 1 51 35 14 2
49 1 50 34 16 4
50 2 57 26 35 10
51 3 77 30 61 23
52 2 57 29 42 13
53 2 65 26 46 15
54 1 46 34 14 3
55 2 59 32 48 18
56 2 60 27 51 16
57 3 65 30 55 18
58 1 51 33 17 5
59 3 77 36 67 22
60 3 76 30 66 21
61 3 67 30 52 23
62 2 61 28 40 13
63 2 55 24 38 11
64 1 52 34 14 2
65 3 79 36 64 20
66 1 50 35 16 6
67 3 77 28 67 20
68 2 55 26 44 12
69 1 48 30 14 3
70 1 48 34 19 2
71 3 61 26 56 14
72 1 58 40 12 2
73 3 62 28 48 18
74 2 56 30 45 15
75 1 46 32 14 2
76 1 57 44 15 4
77 3 68 34 58 24
78 3 72 30 58 16
79 1 54 34 15 4
80 3 64 31 55 18
81 2 49 24 33 10
82 1 55 42 14 2
83 3 60 22 50 15
84 2 52 27 39 14
85 1 44 29 14 2
86 2 58 27 39 12
87 3 69 32 57 23
88 2 59 30 42 15
89 3 56 26 49 20
90 3 67 25 58 18
91 2 63 23 44 13
92 2 63 25 49 15
93 2 51 25 30 11
94 3 69 31 54 21
95 3 72 36 61 25
96 2 56 29 36 13
97 3 68 30 55 21
98 1 48 30 14 1
99 1 57 38 17 3
100 2 66 30 44 14
101 1 51 37 15 4
102 2 67 30 50 17
103 1 52 41 15 1
104 3 60 30 48 18
105 2 56 27 42 13
106 1 49 31 15 2
107 1 54 39 17 4
108 2 60 34 45 16
109 2 50 20 35 10
110 1 47 32 13 2
111 2 62 29 43 13
112 1 51 34 15 2
113 2 60 22 40 10
114 1 49 31 15 1
115 1 54 37 15 2
116 2 61 28 47 12
117 2 57 28 41 13
118 1 54 39 13 4
119 3 65 32 51 20
120 2 69 31 49 15
121 2 55 25 40 13
122 1 45 23 13 3
123 1 51 38 15 3
124 2 68 28 48 14
125 1 52 35 15 2
126 3 63 33 60 25
127 3 71 30 59 21
128 3 63 29 58 18
129 2 57 30 42 12
130 3 77 26 69 23
131 2 66 29 46 13
132 1 50 34 15 2
133 2 55 24 37 10
134 1 46 31 15 2
135 3 74 28 61 19
136 1 50 35 13 3
137 3 73 29 63 18
138 2 67 31 47 15
139 2 56 30 41 13
140 2 64 29 43 13
141 3 65 30 58 22
142 1 51 35 14 3
143 2 61 29 47 14
144 3 64 27 53 19
145 1 48 34 16 2
146 3 57 25 50 20
147 2 55 23 40 13
148 1 54 34 17 2
149 3 58 28 51 24
150 1 53 37 15 2


总共是三类

典型判别式函数摘要:
类似于提取主成分/公因子,方差的%携带了原始信息的多少百分比
函数1:携带原始信息的99%
函数1:携带原始信息的1%

Wilks的Lambda
:对函数判定有无价值的检验
我们看到两个函数的Sig.<0.05的,所以都有统计意义

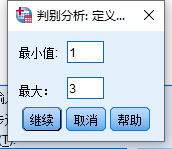
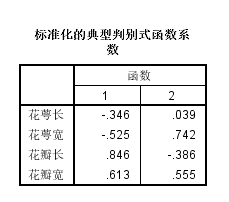
标准化的典型判别式函数系数:
判别函数如何写
函数1=-0.346*花萼长(标准化的)-0.525*花萼宽(标准化的)+0.846*花瓣长(标准化的)+0.613*花瓣宽(标准化的)
函数2同理就不书写了
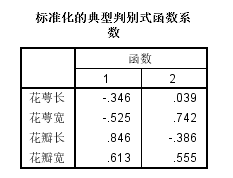
结构矩阵:类似于因子分析里面的载荷,判断函数与变量之间的关联
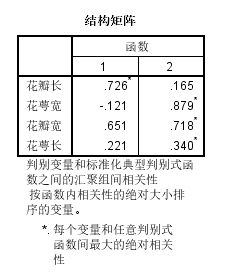
组质心处的函数:各分类对应的中心坐标
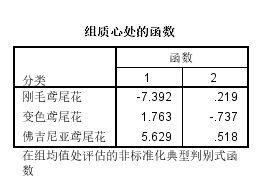
但是这些结果看起来非常枯燥,有图像可以辅助

合并图:三个类别放在一组图

分组图:一个类别一张图



区域图(领域图):类与类之间如何划分?两个质心的垂直平分线(文本图)

验证判别函数好坏
输出–不考虑该个案时的分类(交互验证–刀切法)
由于判别分析师不允许有缺失值的,所以勾选上使用均值替换缺失值,但是缺失值缺失大于10%,不介意这么做

看到其正确率为98%,是相当好的判别函数了

多元正态性的检验(BOX‘s M)

Sig.<0.05证明多元方差齐性是不齐的,证明判别分析适用条件可以违背只要预测效果好就可以
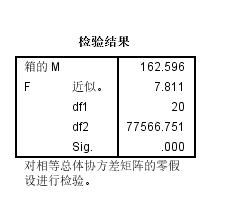
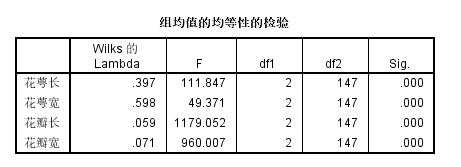
单变量ANOVA:各个自变量在各类别之间是否有差异,四个Sig.<0.05,证明是有差异的
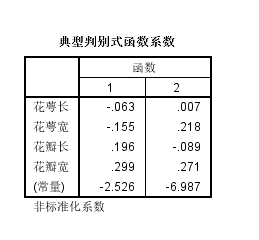
非标准化的判别函数
之前的判别函数都是标准化的,看起来不方便,输出非标准化之前的结果

这个就可以直接写出两个判别函数了,对比一下标化的函数,多了常数项
贝叶斯判别

对每一个类别都会给函数式,扔一个样本进去计算,哪个得分高,算哪一个类,不过这里不改先验概率等参数和典型判别分析结果是一致的

判别分析也可以做变量筛选(不推荐)
一般我们做判别分析前已经做了相关的预分析
