递归求解

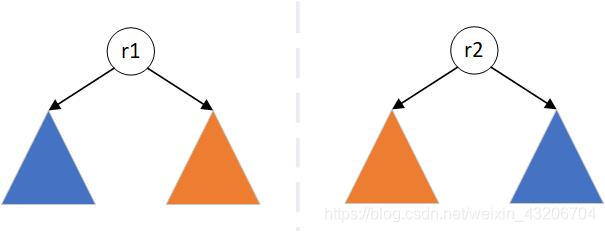
题解的思路为：递归的子问题为判断两棵子树是否是对称的。初始条件如图1所示，根节点肯定是对称的，需要左子树和右子树是否对称。将图一中的左右子树继续拆分，如图2所示，首先判断两棵子树的根节点r1和r2是否相同，再判断根r1的左子树是否和根r2的右子树对称，且根r1的右子树是否和r2的左子树对称。即递归子问题为判断两棵子树是否是对称。

图1







图2

代码如下：

bool DFS(TreeNode* r1, TreeNode* r2)
{
	if (r1 == NULL && r2 == NULL)
		return true;

	if (r1 == NULL || r2 == NULL)
		return false;

	if (r1->val != r2->val)
		return false;

	bool res;
	res = DFS(r1->left, r2->right);
	if (res == false)
		return false;
	res = DFS(r1->right, r2->left);

	return res;
}

bool isSymmetric(TreeNode* root) 
{
	return DFS(root, root);
}

以上的递归子结构有点难想到，结合自己之前的思路有一种更容易理解的方式。之前自己的解法为对左子树进行“左-根-右”遍历，并按顺序保存遍历结果。由于右子树与左子树对称，所以按照“右-根-左”的顺序遍历应该与之前保存的结果是相同，判断左右子树是否对称则判断遍历结果是否相同即可。但是“左-根-右”遍历需要等到“回升”时才能判断，其实如果两根子树对称，则左右子树的“根-左-右”遍历顺序和“根-右-左”的遍历顺序是一样的。这样就不用“回升”，“实时”可以判断。如以上代码，将r1与r2两个参数单独来看，其实就是对r1子树进行“根-左-右”遍历，对r2子树进行“根-右-左”遍历。

队列迭代

题解的第二种方法是使用队列迭代，类似广度优先搜索，由于每次选取一对出队，判断这一对的根节点是否相同，所以入队也按照对称的方式入队，r1的左子树和r2的右子树一对、r1的右子树和r2的左子树一对，思路与上述递归实现类似。

代码如下：

#define QSIZE 100000
TreeNode* Q[QSIZE];

int FRONT, REAR;

bool isSymmetric(TreeNode* root) 
{
	FRONT = REAR = 0;
	Q[REAR] = root;
	REAR = (REAR + 1) % QSIZE;
	Q[REAR] = root;
	REAR = (REAR + 1) % QSIZE;

	TreeNode* lf, *rg;
	while (FRONT != REAR)
	{
		lf = Q[FRONT];
		FRONT = (FRONT + 1) % QSIZE;
		rg = Q[FRONT];
		FRONT = (FRONT + 1) % QSIZE;

		if (lf == NULL && rg == NULL)
			continue;

		if (lf == NULL || rg == NULL)
			return false;

		if (lf->val != rg->val)
			return false;

		Q[REAR] = lf->left;
		REAR = (REAR + 1) % QSIZE;
		Q[REAR] = rg->right;
		REAR = (REAR + 1) % QSIZE;

		Q[REAR] = lf->right;
		REAR = (REAR + 1) % QSIZE;
		Q[REAR] = rg->left;
		REAR = (REAR + 1) % QSIZE;
	}

	return true;
}