相关概念介绍:
这里的相关概念引用的是yxc大佬的讲解,在这里特别感谢yxc大佬的算法课,让我入了算法竞赛的门。
1.1:流网络:G=(V,E)
特点:是一个有向图,且可以有环,不考虑反向边(即使有反向边,也可以通过加点来把一条反向边,变成两条单向边)。
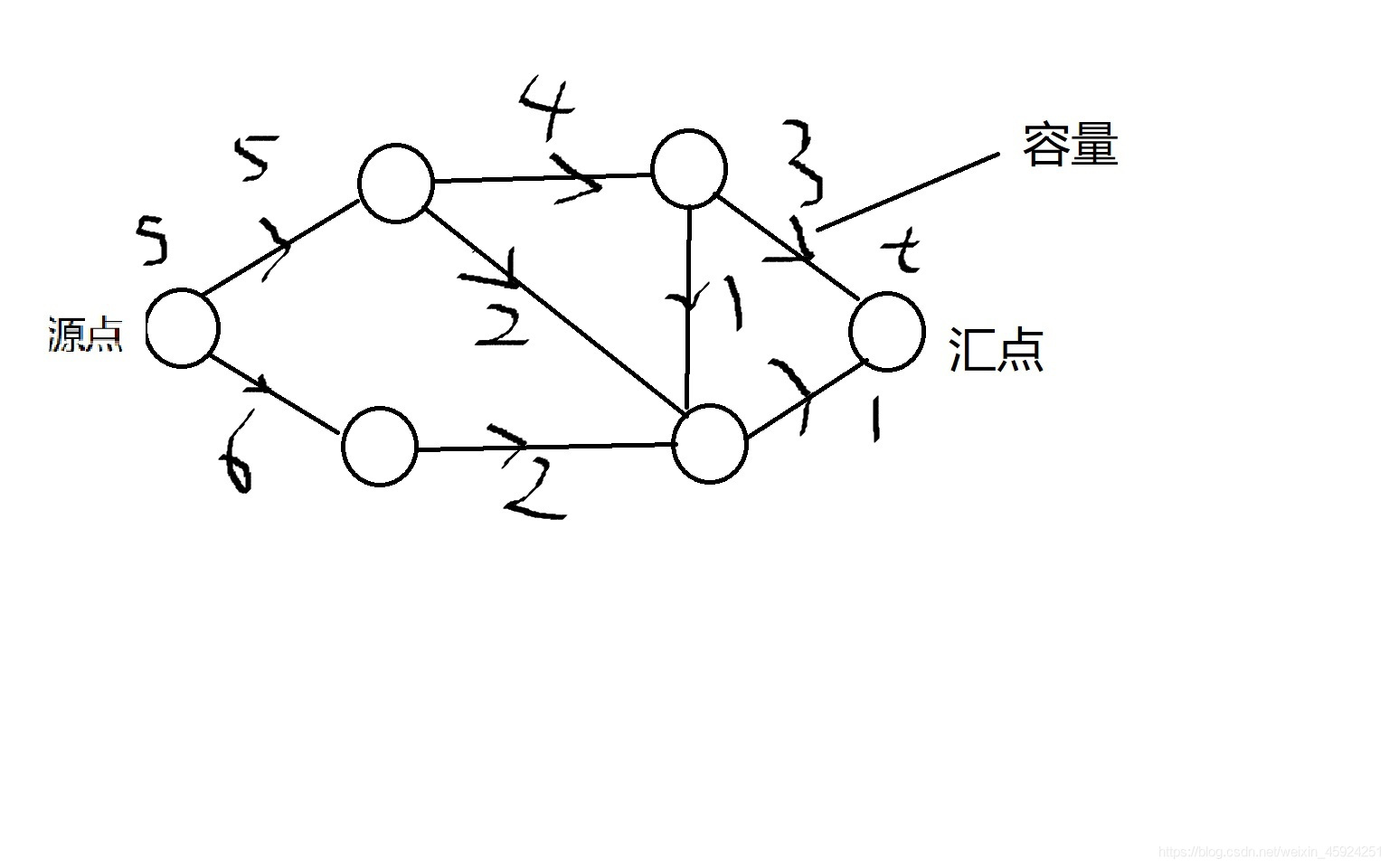
组成:源点,容量,汇点。
源点可以认为是起点,类比与水库,可以源源不断地向外输水。
容量可以理解为离散数学的边权,类比与流速即单位时间内流过的最大的水量的大小。如果边不存在则认为容量是0。
汇点可以认为是终点,类比与大海,从水库里流出来的水,会源源不断的流向大海。
1.2:可行流:f(u,v)
描述:可行流是人为的指定的一条边,让它有你设定的流量。
特点:不需要考虑反向边
条件:当同时满足以下两个条件时,这条边可以成为可行流。
1.容量限制:也就是说你设定的流量不能够超过容量。即0<=f(u,v)<=C(u,v)
2.流量守恒:我们规定除了源点和汇点都不能储存流量,也就是说除了源点和汇点,剩下的节点都应该入多少流量,出多少流量,达到流量守恒:a+b+c=d+e+f
定义大小:|f|=每秒流出源点的总流量-每秒流入汇点的总流量(一般情况下只有流出,没有流入)
注:
1.它虽然是人为定义的,但是是可以计算的。
2.可行流不是指的某一个边,或者某一个点,而是有一个点的进入的流量等于流出的流量,将这些流入流出的边,抽象成一个可行流(满足可行流的两个条件)
3.一个流网络可以有无数个可行流,因为我们的数值不一定取整数
最大流:
对于一个流网络来说会有非常多的可行流,每一个可行流都可以求出一个流量值,这些流量值构成的集合中,流量最大的那个,就是最大流,
即最大可行流。
残留网络:Gf
描述:针对流网络的一条可行流来说,所以可行流不同的话,残留网络也不同。
特点:
1.与可行流一一对应
2.考虑反向边
定义:残留网络中的点的点集和原图完全相同,但是边集不仅包含原图的所有边,还包含了原图中所有边的反向边,即包含两倍的边集(残留网络也是流网络,所以具备流网络的相应组成元素)
边:
1.正向边的容量:是指在原图容量下,除去已经流入的流量而剩下的流量,等于原图该边容量减去原图该边流量,意在还能增加多少流量。
2.反向边的容量:是指在原图该边的流量的基础上,表示退流的流量,退流就是反向流的流量,这个流量等于原图该边的流量(水管里有多少水就可以退多少水),意在减少流量。
残留网络可行流定理:原网络的可行流+其对应的残留网络的可行流仍然等于原网络的一个新的可行流,所以新的可行流的流量值=原可行流的流量值+其对应的残留网络可行流的流量值。
性质:在残留网络中每有一个流量不为0的可行流都可以增加原网络的可行流,即|f’+f|=|f|+|f’|,其中f与f‘是一一对应的关系,而不是任意的两个从原网络和残存网络取出的可行流
推论:
1.如果残留网络中含有流量不为0的可行流的话,原网络的可行流一定不是最大流,反过来,如果残留网络中没有含有流量大于等于0的可行流,原网络的可行流也不一定是最大流。
2.如果残留网络中没有可行流,则原网络中的可行流一定是最大流。


1.3:增广路径:
描述:在残存网络中,从源点开始,沿着容量大于0的边,能够到达汇点的路径,称为增广路径。(一般的增广路径没有环,只是简单的路径)
特点:增广路径一定是可行流。
定理:如果在原网络中的一个可行流,由这个可行流构造出的残留网络中没有增广路径,那么这个可行流必然是原网络中的最大可行流即最大流。
1.4:割:
描述:图网络G=(V,E)我们将图网络的点集V分为两个集合:S和T,其中S和T的关系是:S与T的交集为空集,S与T的并集是点集V,其中源点s是S的元素,汇点t是T的元素,我们把划分后的结果S和T称为割,注意S和T的点集不一定联通。
割的方式:2^(n-2)种
割的容量:是S到T中所有的边的容量之和,如果有T到S的则不计入割的容量之中(不考虑反向边),C(S,T).
如果一个流网络确定了,那么割的容量也确定。
最小割:指的是最小割的容量。
割的流量:所有从S到T的边的流量减去从T到S的边的流量。(考虑反向边)f(S,T).
对于不同的可行流,割的流量是不同的。
割的定理:
1.割的流量一定小于等于割的容量
f(S,T)小于等于C(S,T).
2.流网络的任意一个可行流和割的流量,一定有可行流的流量等于割的流量。
f(S,T)=|f|
割的性质:
- f(X,Y)=-f(Y,X)
- f(X,X)=0;
- 如果X和Y没有交集,则f(Z,X∪Y)=f(Z,X)+f(Z,Y)
-
果X和Y没有交集,则f(X∪Y,Z)=f(Z,X)+f(Z,Y)
结论:
对于任意一个网络流的可行流的流量等于割的流量小于等于割的容量:|f|<=C(S,T);
所以最大可行流一定小于等于最小割的流量
注:在考虑割中的边的时候使用的是原网络中的边的关系

1.5:最大流最小割定理:
可以通过两个推出一个,或者一个推出两个:
- 可行流f是最大可行流。
- 可行流f的残留网络不包含增广路径
- 存在一个割使得这个割的容量等于可行流的流量
其中可行流f是最大流则可行流f的残留网络必然不包含增广路径,而如果一个可行流f的残留网络不包含增广路径,这个可行流f不一定是最大流,需要借助定理3去证明