蓝桥杯
2020年国赛真题(Java 大学 B 组 )
先挂上,闲下来再写,感觉自己开了好多坑
#A 美丽的 2
本题总分:5 分
问题描述
小蓝特别喜欢
2
2
2
,今年是公元
2020
2020
2
0
2
0
年,他特别高兴。
他很好奇,在公元
1
1
1
年到公元
2020
2020
2
0
2
0
年(包含)中,有多少个年份的数位中包含数字
2
2
2
?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
563
calcCode:
public class Test {
public static void main(String[] args) {
int n = 2020, res = 0;
for (int i = 1; i <= n; i++)
if (check(i)) res++;
System.out.println(res);
}
static boolean check(int n) {
do if (n % 10 == 2) return true;
while ((n /= 10) > 0);
return false;
}
}
友好
#B 扩散
本题总分:5 分
问题描述
小蓝在一张无限大的特殊画布上作画。
这张画布可以看成一个方格图,每个格子可以用一个二维的整数坐标表示。
小蓝在画布上首先点了一下几个点:(
0
0
0
,
0
0
0
),(
2020
2020
2
0
2
0
,
11
11
1
1
),(
11
11
1
1
,
14
14
1
4
),(
2000
2000
2
0
0
0
,
2000
2000
2
0
0
0
)。只有这几个格子上有黑色,其它位置都是白色的。
每过一分钟,黑色就会扩散一点。具体的,如果一个格子里面是黑色,它就会扩散到上、下、左、右四个相邻的格子中,使得这四个格子也变成黑色(如果原来就是黑色,则还是黑色)。
请问,经过
2020
2020
2
0
2
0
分钟后,画布上有多少个格子是黑色的。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
11157392 || 20312088
calcCode:
public class Test {
static final int n = 2020;
public static void main(String[] args) {
int[][] resource = { {0, 0}, {2020, 11}, {11, 14}, {2000, 2000} };
boolean[][] marked = new boolean[n << 1 | 1][n << 1 | 1];
long res = 0;
for (int k = 0, x, y; k < 4; k++) {
x = resource[k][0];
y = resource[k][1];
for (int i = -n; i <= n; i++) {
if (x + i < 0) continue;
for (int r = n - abs(i), j = -r; j <= r; j++) {
if (x + i < 0 || y + j < 0 || marked[x + i][y + j]) continue;
marked[x + i][y + j] = true;
res++;
}
}
}
System.out.println(res);
}
static int abs(int n) { return n > 0 ? n : -n; }
}
反正比赛的时候我填的是这个结果
但还有人说这里的扩散可以扩散到负坐标,防杠还是写出来吧
public class Test {
static final int n = 2020;
public static void main(String[] args) {
int[][] resource = { {0, 0}, {2020, 11}, {11, 14}, {2000, 2000} };
boolean[][] marked = new boolean[n << 2][n << 2];
long res = 0;
for (int k = 0, x, y; k < 4; k++) {
x = resource[k][0] + n;
y = resource[k][1] + n;
for (int i = -n; i <= n; i++)
for (int r = n - abs(i), j = -r; j <= r; j++) {
if (marked[x + i][y + j]) continue;
marked[x + i][y + j] = true;
res++;
}
}
System.out.println(res);
}
static int abs(int n) { return n > 0 ? n : -n; }
}
#C 阶乘约数
本题总分:10 分
问题描述
定义阶乘
n
!
=
1
×
2
×
3
×
⋅
⋅
⋅
×
n
n! = 1 × 2 × 3 × · · · × n
n
!
=
1
×
2
×
3
×
⋅
⋅
⋅
×
n
。
请问
100
!
100!
1
0
0
!
(
100
100
1
0
0
的阶乘)有多少个约数。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
39001250856960000
calcCode:
import java.math.BigInteger;
public class Test {
public static void main(String[] args) {
BigInteger num = BigInteger.ONE;
for (int i = 1; i <= 100; i++)
num = num.multiply(new BigInteger(String.valueOf(i)));
long res = 1;
for (BigInteger i = new BigInteger("2"); i.multiply(i).compareTo(num) <= 0; i = i.add(BigInteger.ONE)) {
long cnt = 1;
while (num.mod(i).compareTo(BigInteger.ZERO) == 0) {
num = num.divide(i);
cnt++;
}
if (cnt > 1)
res *= cnt;
}
if (num.compareTo(BigInteger.ONE) > 0) res <<= 1;
System.out.println(res);
}
}
算术基本定理求约数个数
再给你们一个模板
public class Test {
public static void main(String[] args) { System.out.println(factors(100)); }
static int factors(long n) {
int res = 1, now;
for (int i = 2; i * i <= n; i++) {
now = 1;
while (n % i == 0) {
n /= i;
now++;
}
if (now > 1)
res *= now;
}
return n > 1? res << 1 : res;
}
}
最近在学C,C的标准库中没大整形,所以就变换出了这种写法
#include <stdio.h>
#include <string.h>
int main() {
int factor[100];
long long res = 1;
memset(factor, 0x00, sizeof(factor));
for (int i = 100, n = 100; i; n = --i)
for (int k = 2; k <= n; k++)
while (!(n % k)) {
factor[k]++;
n /= k;
}
for (int i = 0; i < 100; i++)
res *= factor[i] + 1;
printf("%lld", res);
}
#D 本质上升序列
本题总分:10 分
问题描述
小蓝特别喜欢单调递增的事物。
在一个字符串中,如果取出若干个字符,将这些字符按照在字符串中的顺序排列后是单调递增的,则成为这个字符串中的一个单调递增子序列。
例如,在字符串 lanqiao 中,如果取出字符 n 和 q,则 nq 组成一个单调递增子序列。类似的单调递增子序列还有 lnq、i、ano 等等。
小蓝发现,有些子序列虽然位置不同,但是字符序列是一样的,例如取第二个字符和最后一个字符可以取到 ao,取最后两个字符也可以取到 ao。小蓝认为他们并没有本质不同。
对于一个字符串,小蓝想知道,本质不同的递增子序列有多少个?
例如,对于字符串 lanqiao,本质不同的递增子序列有 21 个。它们分别是 l、a、n、q、i、o、ln、an、lq、aq、nq、ai、lo、ao、no、io、lnq、anq、lno、ano、aio。
请问对于以下字符串(共 200 个小写英文字母,分四行显示):(如果你把以下文字复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 inc.txt,内容与下面的文本相同)
tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf
iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij
gihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmad
vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl
本质不同的递增子序列有多少个?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
3616159
calcCode:
import java.io.IOException;
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.util.HashSet;
import java.util.Set;
public class Test {
public static void main(String[] args) throws IOException {
System.setIn(new FileInputStream("inc.txt"));
String str = new BufferedReader(new InputStreamReader(System.in)).readLine();
Set set = new HashSet();
dfs(0, '\0', str, new StringBuilder(), set);
set.remove("");
System.out.println(set.size());
}
static void dfs(int cur, char last, String str, StringBuilder buff, Set<String> set) {
if (cur == str.length()) set.add(buff.toString());
else {
dfs(cur + 1, last, str, buff, set);
if (str.charAt(cur) > last) {
int tmp = buff.length();
buff.append(str.charAt(cur));
dfs(cur + 1, str.charAt(cur), str, buff, set);
buff.deleteCharAt(tmp);
}
}
}
}
看了下数据规模,就直接开个线程暴搜了
讲武德的一般都上动规
import java.io.IOException;
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.InputStreamReader;
public class Test {
public static void main(String[] args) throws IOException {
System.setIn(new FileInputStream("inc.txt"));
String str = new BufferedReader(new InputStreamReader(System.in)).readLine();
int[][] dp = new int[201][27];
for (int i = 0; i < 200; i++)
dp[i + 1][str.charAt(i) - 'a' + 1] = 1;
for (int i = 1; i <= 200; i++) {
int now = str.charAt(i - 1) - 'a' + 1;
for (int j = 1; j <= 26; j++)
dp[i][j] = dp[i - 1][j];
dp[i][now] = 1;
for (int j = 1; j < now; j++)
dp[i][now] += dp[i - 1][j];
}
long res = 0;
for (int i = 1; i <= 26; i++)
res += dp[200][i];
System.out.println(res);
}
}
#E 玩具蛇
本题总分:15 分
问题描述
小蓝有一条玩具蛇,一共有
16
16
1
6
节,上面标着数字
1
1
1
至
16
16
1
6
。每一节都是一个正方形的形状。相邻的两节可以成直线或者成
90
90
9
0
度角。
小蓝还有一个
4
×
4
4 × 4
4
×
4
的方格盒子,用于存放玩具蛇,盒子的方格上依次标着字母
A
A
A
到
P
P
P
共
16
16
1
6
个字母。
小蓝可以折叠自己的玩具蛇放到盒子里面。他发现,有很多种方案可以将玩具蛇放进去。
下图给出了两种方案:
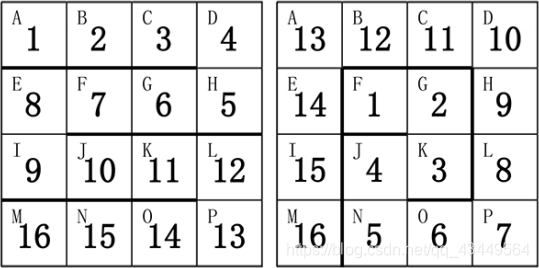
请帮小蓝计算一下,总共有多少种不同的方案。如果两个方案中,存在玩
具蛇的某一节放在了盒子的不同格子里,则认为是不同的方案。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
552
calcCode:
public class Test {
public static void main(String[] args) {
Counter res = new Counter();
int[] offset = { -1, 0, 1, 0, -1 };
boolean[][] marked = new boolean[4][4];
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++) {
marked[i][j] = true;
dfs(i, j, 1, offset, marked, res);
marked[i][j] = false;
}
System.out.println(res.tally());
}
static void dfs(int x, int y, int cur, int[] offset, boolean[][] marked, Counter cnt) {
if (cur == 16) cnt.increment();
else
for (int k = 0, i, j; k < 4; k++) {
i = x + offset[k];
j = y + offset[k + 1];
if (i < 0 || i >= 4 || j < 0 || j >= 4 || marked[i][j]) continue;
marked[i][j] = true;
dfs(i, j, cur + 1, offset, marked, cnt);
marked[i][j] = false;
}
}
static class Counter {
int cnt;
void increment() { cnt++; }
int tally() { return cnt; }
}
}
不知道怎么去优化,就分头搜索算球
#F 蓝肽子序列
时间限制: 1.0s 内存限制: 512.0MB 本题总分:15 分
问题描述
L
L
L
星球上的生物由蛋蓝质组成,每一种蛋蓝质由一类称为蓝肽的物资首尾连接成一条长链后折叠而成。
生物学家小乔正在研究
L
L
L
星球上的蛋蓝质。她拿到两个蛋蓝质的蓝肽序列,想通过这两条蓝肽序列的共同特点来分析两种蛋蓝质的相似性。
具体的,一个蓝肽可以使用
1
1
1
至
5
5
5
个英文字母表示,其中第一个字母大写,后面的字母小写。一个蛋蓝质的蓝肽序列可以用蓝肽的表示顺序拼接而成。
在一条蓝肽序列中,如果选取其中的一些位置,把这些位置的蓝肽取出,并按照它们在原序列中的位置摆放,则称为这条蓝肽的一个子序列。蓝肽的子序列不一定在原序列中是连续的,中间可能间隔着一些未被取出的蓝肽。
如果第一条蓝肽序列可以取出一个子序列与第二条蓝肽序列中取出的某个子序列相等,则称为一个公共蓝肽子序列。
给定两条蓝肽序列,找出他们最长的那个公共蓝肽子序列的长度。
输入格式
输入两行,每行包含一个字符串,表示一个蓝肽序列。字符串中间没有空格等分隔字符。
输出格式
输出一个整数,表示最长的那个公共蓝肽子序列的长度。
测试样例
1
Input:
LanQiaoBei
LanTaiXiaoQiao
Output:
2
Explanation:
最长的公共蓝肽子序列为 LanQiao,共两个蓝肽。
评测用例规模与约定
对于
20
20
2
0
% 的评测用例,两个字符串的长度均不超过
20
20
2
0
。
对于
50
50
5
0
% 的评测用例,两个字符串的长度均不超过
100
100
1
0
0
。
对于所有评测用例,两个字符串的长度均不超过
1000
1000
1
0
0
0
。
code:
import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.HashMap;
import java.util.Map;
public class Main {
static int[] A, B;
static int n, m, MAX = 0, cur;
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
Map<String, Integer> map = new HashMap();
String Astr = in.readLine();
String Bstr = in.readLine();
A = new int[1024];
B = new int[1024];
Integer val;
String key;
if (Astr.length() > Bstr.length()) {
String t = Bstr;
Bstr = Astr;
Astr = t;
}
for (int start = 0, end, high = Astr.length(); start < high; start = end) {
end = start + 1;
while(end < high && Astr.charAt(end) > 'Z') end++;
key = Astr.substring(start, end);
val = map.get(key);
if (val == null)
map.put(key, val = cur++);
A[n++] = val;
}
for (int start = 0, end, high = Bstr.length(); start < high; start = end) {
end = start + 1;
while(end < high && Bstr.charAt(end) > 'Z') end++;
key = Bstr.substring(start, end);
val = map.get(key);
if (val != null)
B[m++] = val;
}
dfs(0, 0, 0);
System.out.println(MAX);
}
static void dfs(int Acur, int Bcur, int val) {
if (Acur < n) {
dfs(Acur + 1, Bcur, val);
while (Bcur < m && A[Acur] != B[Bcur]) Bcur++;
if (Bcur < m) dfs(Acur + 1, Bcur, val + 1);
} else if (val > MAX) MAX = val;
}
}
一眼就能知道是最长公共子序列问题,但好巧不巧
不会
所以比赛现场用的压缩减独加上暴搜,骗个五十分应该没啥问题
再上个现学的动规
import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.HashMap;
import java.util.Map;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
Map<String, Integer> map = new HashMap();
String Astr = in.readLine();
String Bstr = in.readLine();
int n = 1, m = 1, cur = 1;
int[] A = new int[1024];
int[] B = new int[1024];
Integer val;
String key;
if (Astr.length() > Bstr.length()) {
String t = Bstr;
Bstr = Astr;
Astr = t;
}
for (int start = 0, end, high = Astr.length(); start < high; start = end) {
end = start + 1;
while(end < high && Astr.charAt(end) > 'Z') end++;
key = Astr.substring(start, end);
val = map.get(key);
if (val == null)
map.put(key, val = cur++);
A[n++] = val;
}
for (int start = 0, end, high = Bstr.length(); start < high; start = end) {
end = start + 1;
while(end < high && Bstr.charAt(end) > 'Z') end++;
key = Bstr.substring(start, end);
val = map.get(key);
if (val != null)
B[m++] = val;
}
int[][] dp = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
dp[i][j] = A[i] == B[j] ? dp[i - 1][j - 1] + 1 : max(dp[i - 1][j], dp[i][j - 1]);
System.out.println(dp[n][m] - 1);
}
static int max(int a, int b) { return a > b ? a : b; }
}
d
p
[
i
,
j
]
=
{
0
i
=
0
o
r
j
=
0
d
p
[
i
−
1
]
[
j
−
1
]
+
1
S
1
i
=
S
2
j
m
a
x
(
d
p
[
i
−
1
]
[
j
]
,
d
p
[
i
]
[
j
−
1
]
)
dp[i, j]=\left\{ \begin{array}{l|r} 0&i = 0\:or\:j = 0\\ dp[i – 1][j – 1] + 1&S1_{i} = S2_{j}\\ max(dp[i – 1][j], dp[i][j – 1]) \end{array} \right.
d
p
[
i
,
j
]
=
⎩
⎨
⎧
0
d
p
[
i
−
1
]
[
j
−
1
]
+
1
m
a
x
(
d
p
[
i
−
1
]
[
j
]
,
d
p
[
i
]
[
j
−
1
]
)
i
=
0
o
r
j
=
0
S
1
i
=
S
2
j
#G 皮亚诺曲线距离
时间限制: 1.0s 内存限制: 512.0MB 本题总分:20 分
问题描述
皮亚诺曲线是一条平面内的曲线。
下图给出了皮亚诺曲线的
1
1
1
阶情形,它是从左下角出发,经过一个
3
×
3
3 × 3
3
×
3
的方格中的每一个格子,最终到达右上角的一条曲线。

下图给出了皮亚诺曲线的
2
2
2
阶情形,它是经过一个
3
2
×
3
2
3^{2} × 3^{2}
3
2
×
3
2
的方格中的每一个格子的一条曲线。它是将
1
1
1
阶曲线的每个方格由
1
1
1
阶曲线替换而成。

下图给出了皮亚诺曲线的
3
3
3
阶情形,它是经过一个
3
3
×
3
3
3^{3} × 3^{3}
3
3
×
3
3
的方格中的每一个格子的一条曲线。它是将
2
2
2
阶曲线的每个方格由
1
1
1
阶曲线替换而成。

皮亚诺曲线总是从左下角开始出发,最终到达右上角。
我们将这些格子放到坐标系中,对于 k 阶皮亚诺曲线,左下角的坐标是
(
0
0
0
,
0
0
0
),右上角坐标是 (
3
k
−
1
3^{k} − 1
3
k
−
1
,
3
k
−
1
3^{k} − 1
3
k
−
1
),右下角坐标是 (
3
k
−
1
3^{k} − 1
3
k
−
1
,
0
0
0
),左上角坐标是(
0
0
0
,
3
k
−
1
3^{k} − 1
3
k
−
1
)。
给定 k 阶皮亚诺曲线上的两个点的坐标,请问这两个点之间,如果沿着皮亚诺曲线走,距离是到少?
输入格式
输入的第一行包含一个正整数
k
k
k
,皮亚诺曲线的阶数。
第二行包含两个整数
x
1
x_{1}
x
1
,
y
1
y_{1}
y
1
,表示第一个点的坐标。
第三行包含两个整数
x
2
x_{2}
x
2
,
y
2
y_{2}
y
2
,表示第二个点的坐标。
输出格式
输出一个整数,表示给定的两个点之间的距离。
测试样例
1
Input:
1
0 0
2 2
Output:
8
测试样例
2
Input:
2
0 2
0 3
Output:
13
评测用例规模与约定
对于
30
30
3
0
% 的评测用例,
0
≤
k
≤
10
0 ≤ k ≤ 10
0
≤
k
≤
1
0
。
对于
50
50
5
0
% 的评测用例,
0
≤
k
≤
20
0 ≤ k ≤ 20
0
≤
k
≤
2
0
。
对于所有评测用例,
0
≤
k
≤
100
,
0
≤
x
1
,
y
1
,
x
2
,
y
2
<
3
k
,
x
1
,
y
1
,
x
2
,
y
2
≤
1
0
18
0 ≤ k ≤ 100, 0 ≤ x_{1}, y_{1}, x_{2}, y_{2} < 3^{k}, x1, y1, x2, y2 ≤ 10^{18}
0
≤
k
≤
1
0
0
,
0
≤
x
1
,
y
1
,
x
2
,
y
2
<
3
k
,
x
1
,
y
1
,
x
2
,
y
2
≤
1
0
1
8
。
数据保证答案不超过
1
0
18
10^{18}
1
0
1
8
。
code:
// 不会
#H 画廊
时间限制: 1.0s 内存限制: 512.0MB 本题总分:20 分
问题描述
小蓝办了一个画展,在一个画廊左右两边陈列了他自己的作品。为了使画展更有意思,小蓝没有等距陈列自己的作品,而是按照更有艺术感的方式陈列。
在画廊的左边陈列了
L
L
L
幅作品,在画廊的右边陈列了
R
R
R
幅作品,左边的作品距离画廊的起点依次为 u
1
, u
2
, · · · , u
L
,右边的作品距离画廊起点依次为 v
1
, v
2
, · · · , v
R
。
每周,小蓝要整理一遍自己的每一幅作品。整理一幅作品的时间是固定的,但是要带着沉重的工具。从一幅作品到另一幅作品之间的距离为直线段的长度。
小蓝从画廊的起点的正中央(左右两边的中点)出发,整理好每一幅画,最终到达画廊的终点的正中央。已知画廊的宽为
w
w
w
。
请问小蓝最少带着工具走多长的距离?
输入格式
输入的第一行包含四个整数
L
,
R
,
d
,
w
L, R, d, w
L
,
R
,
d
,
w
,表示画廊左边和右边的作品数量,
以及画廊的长度和宽度。
第二行包含
L
L
L
个正整数 u
1
, u
2
, · · · , u
L
,表示画廊左边的作品的位置。
第三行包含
R
R
R
个正整数 v
1
, v
2
, · · · , v
R
,表示画廊右边的作品的位置。
输出格式
输出一个实数,四舍五入保留两位小数,表示小蓝最少带着工具走的距离。
测试样例
1
Input:
3 3 10 2
1 3 8
2 4 6
Output:
14.71
Explanation:
小蓝从起点开始,首先到达左边第一幅作品(走动距离 √2),然后到达左
边第二幅作品(走动距离 2),然后到达右边第一幅作品(走动距离 √5),然后
到达右边第二幅和第三幅作品(走动距离 2 和 2),然后到达左边第三幅作品(走动距离 2√2),最后到达画廊终点(走动距离 √5)。
总共距离为 √2 + 2 + √5 + 2 + 2 + 2 √2 + √5 ≈ 14.71。
评测用例规模与约定
对于
40
40
4
0
% 的评测用例,
1
≤
L
,
R
≤
10
,
1
≤
d
≤
100
,
1
≤
w
≤
100
1 ≤ L, R ≤ 10, 1 ≤ d ≤ 100, 1 ≤ w ≤ 100
1
≤
L
,
R
≤
1
0
,
1
≤
d
≤
1
0
0
,
1
≤
w
≤
1
0
0
。
对于
70
70
7
0
% 的评测用例,
1
≤
L
,
R
≤
100
,
1
≤
d
≤
1000
,
1
≤
w
≤
1000
1 ≤ L, R ≤ 100, 1 ≤ d ≤ 1000, 1 ≤ w ≤ 1000
1
≤
L
,
R
≤
1
0
0
,
1
≤
d
≤
1
0
0
0
,
1
≤
w
≤
1
0
0
0
。
对于所有评测用例,
1
≤
L
,
R
≤
500
,
1
≤
d
≤
100000
,
1
≤
w
≤
100000
,
0
≤
1 ≤ L, R ≤ 500, 1 ≤ d ≤ 100000, 1 ≤ w ≤ 100000,0 ≤
1
≤
L
,
R
≤
5
0
0
,
1
≤
d
≤
1
0
0
0
0
0
,
1
≤
w
≤
1
0
0
0
0
0
,
0
≤
u
1
<
<
<
u
2
<
⋅
⋅
⋅
<
< · · · <
<
⋅
⋅
⋅
<
u
L
≤
d
,
0
≤
≤ d, 0 ≤
≤
d
,
0
≤
v
1
<
<
<
v
2
<
⋅
⋅
⋅
<
< · · · <
<
⋅
⋅
⋅
<
v
R
≤
d
≤ d
≤
d
。
code:
import java.io.IOException;
import java.io.BufferedReader;
import java.io.StreamTokenizer;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
public class Main {
public static void main(String[] args) throws IOException {
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
int L, R, d, w;
in.nextToken();
L = (int)in.nval;
in.nextToken();
R = (int)in.nval;
in.nextToken();
d = (int)in.nval;
in.nextToken();
w = (int)in.nval;
int[] left = new int[L + 1];
int[] right = new int[R + 1];
for (int i = 1; i <= L; i++) {
in.nextToken();
left[i] = (int)in.nval;
}
for (int i = 1; i <= R; i++) {
in.nextToken();
right[i] = (int)in.nval;
}
double ww = w * w;
double[][][] visit = new double[2][L + 1][R + 1];
double mm = w * w / 4.0, res = Double.POSITIVE_INFINITY;
double llast = Math.sqrt((d - left[L]) * (d - left[L]) + mm),
rlast = Math.sqrt((d - right[R]) * (d - right[R]) + mm);
Step now, next;
Queue<Step> queue = new LinkedList();
queue.offer(new Step(visit[0][1][0] = Math.sqrt(mm + left[1] * left[1]), 1, 0, true));
queue.offer(new Step(visit[1][0][1] = Math.sqrt(mm + right[1] * right[1]), 0, 1, false));
while (queue.size() > 0) {
now = queue.poll();
if (now.l == L && now.r == R) {
now.len += now.here ? llast : rlast;
if (now.len < res) res = now.len;
continue;
}
if (now.l < L) {
if (now.here) next = new Step(now.len + Math.sqrt((left[now.l + 1] - left[now.l]) * (left[now.l + 1] - left[now.l])), now.l + 1, now.r, true);
else next = new Step(now.len + Math.sqrt(ww + (left[now.l + 1] - right[now.r]) * (left[now.l + 1] - right[now.r])), now.l + 1, now.r, true);
if (visit[0][next.l][next.r] == 0 || visit[0][next.l][next.r] > now.len) {
visit[0][next.l][next.r] = now.len;
queue.offer(next);
}
}
if (now.r < R) {
if (now.here) next = new Step(now.len + Math.sqrt(ww + (right[now.r + 1] - left[now.l]) * (right[now.r + 1] - left[now.l])), now.l, now.r + 1, false);
else next = new Step(now.len + Math.sqrt((right[now.r + 1] - right[now.r]) * (right[now.r + 1] - right[now.r])), now.l, now.r + 1, false);
if (visit[1][next.l][next.r] == 0 || visit[1][next.l][next.r] > now.len) {
visit[1][next.l][next.r] = now.len;
queue.offer(next);
}
}
}
System.out.printf("%.2f\n", res);
}
static class Step {
int l, r;
boolean here;
double len;
Step(double len, int l, int r, boolean here) {
this.l = l;
this.r = r;
this.len = len;
this.here = here;
}
}
}
应该是道特殊的最小树生成
但比赛的时候广搜写一半才发现的
自信不会超时就没改
#I 补给
时间限制: 3.0s 内存限制: 512.0MB 本题总分:25 分
问题描述
小蓝是一个直升飞机驾驶员,他负责给山区的
n
n
n
个村庄运送物资。每个月,他都要到每个村庄至少一次,可以多于一次,将村庄需要的物资运送过去。每个村庄都正好有一个直升机场,每两个村庄之间的路程都正好是村庄之间的直线距离。
由于直升机的油箱大小有限,小蓝单次飞行的距离不能超过
D
D
D
。每个直升机场都有加油站,可以给直升机加满油。
每个月,小蓝都是从总部出发,给各个村庄运送完物资后回到总部。如果方便,小蓝中途也可以经过总部来加油。
总部位于编号为
1
1
1
的村庄。
请问,要完成一个月的任务,小蓝至少要飞行多长距离?
输入格式
输入的第一行包含两个整数
n
n
n
,
D
D
D
,分别表示村庄的数量和单次飞行的距离。
接下来 n 行描述村庄的位置,其中第
i
i
i
行两个整数
x
i
x_{i}
x
i
,
y
i
y_{i}
y
i
,表示编号为
i
i
i
的村庄的坐标。村庄 i 和村庄 j 之间的距离为
(
x
i
−
x
j
)
2
+
(
y
i
−
y
j
)
2
\sqrt{(x_{i} − x_{j})^{2} + (y_{i} − y_{j})^{2}}
(
x
i
−
x
j
)
2
+
(
y
i
−
y
j
)
2
。
输出格式
输出一行,包含一个实数,四舍五入保留正好
2
2
2
位小数,表示答案。
测试样例
1
Input:
4 10
1 1
5 5
1 5
5 1
Output:
16.00
Explanation:
四个村庄形成一个正方形的形状。
测试样例
2
Input:
4 6
1 1
4 5
8 5
11 1
Output:
28.00
Explanation:
补给顺序为 1 → 2 → 3 → 4 → 3 → 2 → 1。
评测用例规模与约定
对于所有评测用例,
1
≤
n
≤
20
,
1
≤
x
i
,
y
i
≤
1
0
4
,
1
≤
D
≤
1
0
5
1 ≤ n ≤ 20, 1 ≤ x_{i}, y_{i} ≤ 10^{4}, 1 ≤ D ≤ 10^{5}
1
≤
n
≤
2
0
,
1
≤
x
i
,
y
i
≤
1
0
4
,
1
≤
D
≤
1
0
5
。
code:
#J 质数行者
时间限制: 5.0s 内存限制: 512.0MB 本题总分:25 分
问题描述
小蓝在玩一个叫质数行者的游戏。
游戏在一个
n
×
m
×
w
n × m × w
n
×
m
×
w
的立体方格图上进行,从北到南依次标号为第
1
1
1
行到第
n
n
n
行,从西到东依次标号为第
1
1
1
列到第
m
m
m
列,从下到上依次标号为第
1
1
1
层到第
w
w
w
层。
小蓝要控制自己的角色从第
1
1
1
行第
1
1
1
列第
1
1
1
层移动到第
n
n
n
行第
m
m
m
列第
w
w
w
层。每一步,他可以向东走质数格、向南走质数格或者向上走质数格。每走到一个位置,小蓝的角色要稍作停留。
在游戏中有两个陷阱,分别为第
r
1
r_{1}
r
1
行第
c
1
c_{1}
c
1
列第
h
1
h_{1}
h
1
层和第
r
2
r_{2}
r
2
行第
c
2
c_{2}
c
2
列第
h
2
h_{2}
h
2
层。这两个陷阱的位置可以跨过,但不能停留。也就是说,小蓝不能控制角色某一步正好走到陷阱上,但是某一步中间跨过了陷阱是允许的。
小蓝最近比较清闲,因此他想用不同的走法来完成这个游戏。所谓两个走法不同,是指小蓝稍作停留的位置集合不同。
请帮小蓝计算一下,他总共有多少种不同的走法。
提示:请注意内存限制,如果你的程序运行时超过内存限制将不得分。
输入格式
输入第一行包含两个整数
n
,
m
,
w
n, m, w
n
,
m
,
w
,表示方格图的大小。
第二行包含
6
6
6
个整数,
r
1
,
c
1
,
h
1
,
r
2
,
c
2
,
h
2
r_{1}, c_{1}, h_{1}, r_{2}, c_{2}, h_{2}
r
1
,
c
1
,
h
1
,
r
2
,
c
2
,
h
2
,表示陷阱的位置。
输出格式
输出一行,包含一个整数,表示走法的数量。答案可能非常大,请输出答案除以
1000000007
1000000007
1
0
0
0
0
0
0
0
0
7
的余数。
测试样例
1
Input:
5 6 1
3 4 1 1 2 1
Output:
11
Explanation:
用 (r, c, h) 表示第 r 行第 c 列第 h 层,可能的走法有以下几种:
1. (1, 1, 1) − (1, 3, 1) − (1, 6, 1) − (3, 6, 1) − (5, 6, 1)。
2. (1, 1, 1) − (1, 3, 1) − (3, 3, 1) − (3, 6, 1) − (5, 6, 1)。
3. (1, 1, 1) − (1, 3, 1) − (3, 3, 1) − (5, 3, 1) − (5, 6, 1)。
4. (1, 1, 1) − (3, 1, 1) − (3, 3, 1) − (3, 6, 1) − (5, 6, 1)。
5. (1, 1, 1) − (3, 1, 1) − (3, 3, 1) − (5, 3, 1) − (5, 6, 1)。
6. (1, 1, 1) − (3, 1, 1) − (5, 1, 1) − (5, 3, 1) − (5, 6, 1)。
7. (1, 1, 1) − (3, 1, 1) − (5, 1, 1) − (5, 4, 1) − (5, 6, 1)。
8. (1, 1, 1) − (1, 4, 1) − (1, 6, 1) − (3, 6, 1) − (5, 6, 1)。
9. (1, 1, 1) − (1, 6, 1) − (3, 6, 1) − (5, 6, 1)。
10. (1, 1, 1) − (3, 1, 1) − (3, 6, 1) − (5, 6, 1)。
11. (1, 1, 1) − (3, 1, 1) − (5, 1, 1) − (5, 6, 1)。
评测用例规模与约定
对于
30
30
3
0
% 的评测用例
1
≤
n
,
m
,
w
≤
50
1 ≤ n, m,w ≤ 50
1
≤
n
,
m
,
w
≤
5
0
。
对于
60
60
6
0
% 的评测用例
1
≤
n
,
m
,
w
≤
300
1 ≤ n, m,w ≤ 300
1
≤
n
,
m
,
w
≤
3
0
0
。
对于所有评测用例,
1
≤
n
,
m
,
w
≤
1000
,
1
≤
r
1
,
r
2
≤
n
,
1
≤
c
1
,
c
2
≤
m
,
1
≤
h
1
,
h
2
≤
w
1 ≤ n, m, w ≤ 1000,1 ≤ r_{1},r_{2} ≤ n, 1 ≤ c_{1}, c_{2} ≤ m,1 ≤ h_{1}, h_{2} ≤ w
1
≤
n
,
m
,
w
≤
1
0
0
0
,
1
≤
r
1
,
r
2
≤
n
,
1
≤
c
1
,
c
2
≤
m
,
1
≤
h
1
,
h
2
≤
w
,陷阱不在起点或终点,两个陷阱不同。
code:
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStream;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
static final int MOD = 1000000007;
static int p, prime[], dp[][][];
public static void main(String[] args) {
InputReader in = new InputReader(System.in);
int n = in.nextInt(), m = in.nextInt(), v = in.nextInt(),
r1 = in.nextInt(), c1 = in.nextInt(), h1 = in.nextInt(),
r2 = in.nextInt(), c2 = in.nextInt(), h2 = in.nextInt();
dp = new int[n + 1][m + 1][v + 1];
prime = new int[256];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
Arrays.fill(dp[i][j], -1);
dp[r1][c1][h1] = dp[r2][c2][h2] = 0;
dp[1][1][1] = 1;
prime[p++] = 2;
agent: for (int i = 3; i < 1000; i += 2) {
for (int k = 0, h = (int)Math.sqrt(i); prime[k] <= h; k++)
if (i % prime[k] == 0) continue agent;
prime[p++] = i;
}
System.out.println(dfs(n, m, v));
}
static int dfs(int x, int y, int z) {
if (dp[x][y][z] >= 0) return dp[x][y][z];
int res = 0;
for (int i = 0; i < p; i++) {
if (x - prime[i] > 0) res = (res + dfs(x - prime[i], y, z)) % MOD;
if (y - prime[i] > 0) res = (res + dfs(x, y - prime[i], z)) % MOD;
if (z - prime[i] > 0) res = (res + dfs(x, y, z - prime[i])) % MOD;
}
return dp[x][y][z] = res;
}
static class InputReader {
BufferedReader read;
StringTokenizer tok;
String delimiters;
InputReader(InputStream in) { this(in, " \n\t\r\f"); }
InputReader(InputStream in, String delimiters) {
this.read = new BufferedReader(new InputStreamReader(in));
this.delimiters = delimiters;
}
String next() {
while (tok == null || !tok.hasMoreTokens())
try {
tok = new StringTokenizer(read.readLine(), delimiters);
} catch (IOException e) {
e.fillInStackTrace();
}
return tok.nextToken();
}
int nextInt() { return Integer.parseInt(next()); }
}
}
应该是记搜,九折九折