1、算法描述
在括号匹配算法中定义int flag = 1变量来标记匹配结果是成功还是失败!
利用数据结构栈,从左到右依次扫描字符串:
若是遇到左括号入栈;
若是遇到右括号:
若栈非空,使用Pop(s,topElem)操作得到栈顶元素,与当前的右括号进行匹配。若是当前的右括号与栈顶元素不匹配,那么修改flag的值为0,匹配失败,并且打印错误信息!
若栈为空,则说明当前所有扫描的右括号均无法没有左括号与之匹配,修改flag为0,匹配失败,并且打印错误信息!
从左到右扫描完整个字符串之后:
若栈为空且 flag的值为1,即为匹配成功!(因为若是没有flag,那么(]这种情况也是匹配成功!所以算法的逻辑将会产生错误!)
否则其余情况均是匹配失败!
2、具体代码如下
——————————————————————————————————————————————————
//括号匹配算法
#include<stdio.h>
#include<stdlib.h> //malloc函数的头文件
#define MaxSize 20
#include
using namespace std;
#define OK 1;
#define ERROR 0;
//结构体定义
typedef struct{
char *data; //存储空间的基地址
int top; //栈顶指针记录下标
}SqStack;
——————————————————————————————————————————————————
//初始化栈
void InitStack(SqStack &s){
s.data = (char *) malloc(sizeof(char)*MaxSize);
s.top = -1;
}
——————————————————————————————————————————————————
//判断栈是否为空
int SqStackIsEmpty(SqStack s) {
if (s.top == -1)
return OK; //栈空
return ERROR; //栈不为空
}
——————————————————————————————————————————————————
//入栈操作
void Push(SqStack &s,char c){
if(s.top == MaxSize – 1) //栈满
printf(“栈满!\n”);
s.top = s.top + 1;
s.data[s.top] = c;
}
——————————————————————————————————————————————————
//出栈操作
void Pop(SqStack &s, char &c){
if(SqStackIsEmpty(s))
printf(“栈空!\n”);
c = s.data[s.top];
s.top = s.top – 1;
}
——————————————————————————————————————————————————
//括号匹配函数
void bracketCheck(char str[], int length){
SqStack s;
InitStack(s);
int flag = 1; //标志是否匹配成功
for(int i = 0; i<length;i++){
if(str[i] == ‘(’ || str[i] == ‘[’ || str[i] == ‘{’){
Push(s,str[i]); //从左到右扫描,遇见左括号就执行入栈操作
}
else if(str[i] == ‘)’ || str[i] == ‘]’ || str[i] == ‘}’){ //遇见右括号判断栈中符号
if(!SqStackIsEmpty(s))
{
char topElem;
Pop(s,topElem);
if(str[i] == ‘)’ && topElem != ‘(’){
flag = 0;
printf(“匹配失败,第 %d 个右括号 %c 与栈顶符号 %c 不匹配\n”,i+1,str[i],topElem);
}
if(str[i] == ‘]’ && topElem != ‘[’){
flag = 0;
printf(“匹配失败,第 %d 个右括号 %c 与栈顶符号 %c 不匹配\n”,i+1,str[i],topElem);
}
if(str[i] == ‘}’ && topElem != ‘{’){
flag = 0;
printf(“匹配失败,第 %d 个右括号 %c 与栈顶符号 %c 不匹配\n”,i+1,str[i],topElem);
}
}
else {
printf(“\n匹配失败,第 %d 个是单身右括号 %c \n”,i+1,str[i]); //栈空,存在单身右括号
flag = 0;
}
}
}
if(SqStackIsEmpty(s) && flag == 1){
printf(“\n匹配成功!!!\n”);
}
else printf(“\n匹配失败!!!\n”);
}
——————————————————————————————————————————————————
//主函数
int main(){
char str[MaxSize] = “\0”; //字符数组初始化\0
//puts(str);
printf(“请输入您要判断的表达式:\t”);
gets(str);
printf(“\n”);
bracketCheck(str,MaxSize);
}
——————————————————————————————————————————————————
3、核心代码
——————————————————————————————————————————————————
//括号匹配函数
void bracketCheck(char str[], int length){
SqStack s;
InitStack(s);
int flag = 1; //标志是否匹配成功
for(int i = 0; i<length;i++){
if(str[i] == ‘(’ || str[i] == ‘[’ || str[i] == ‘{’){
Push(s,str[i]); //从左到右扫描,遇见左括号就执行入栈操作
}
else if(str[i] == ‘)’ || str[i] == ‘]’ || str[i] == ‘}’){ //遇见右括号判断栈中符号
if(!SqStackIsEmpty(s))
{
char topElem;
Pop(s,topElem);
if(str[i] == ‘)’ && topElem != ‘(’){
flag = 0;
printf(“匹配失败,第 %d 个右括号 %c 与栈顶符号 %c 不匹配\n”,i+1,str[i],topElem);
}
if(str[i] == ‘]’ && topElem != ‘[’){
flag = 0;
printf(“匹配失败,第 %d 个右括号 %c 与栈顶符号 %c 不匹配\n”,i+1,str[i],topElem);
}
if(str[i] == ‘}’ && topElem != ‘{’){
flag = 0;
printf(“匹配失败,第 %d 个右括号 %c 与栈顶符号 %c 不匹配\n”,i+1,str[i],topElem);
}
}
else {
printf(“\n匹配失败,第 %d 个是单身右括号 %c \n”,i+1,str[i]); //栈空,存在单身右括号
flag = 0;
}
}
}
if(SqStackIsEmpty(s) && flag == 1){
printf(“\n匹配成功!!!\n”);
}
else printf(“\n匹配失败!!!\n”);
}
如果不使用c语言,上面的入栈、退栈等各种操作可以使用c++、java中自定义好的栈来直接操作,简化代码!
——————————————————————————————————————————————————
4、代码演示
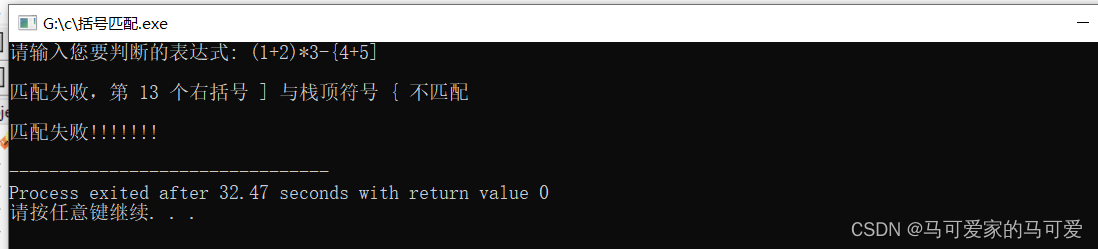
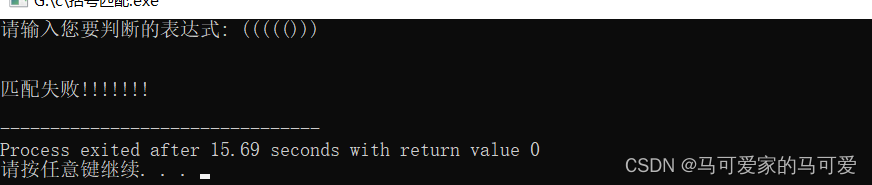
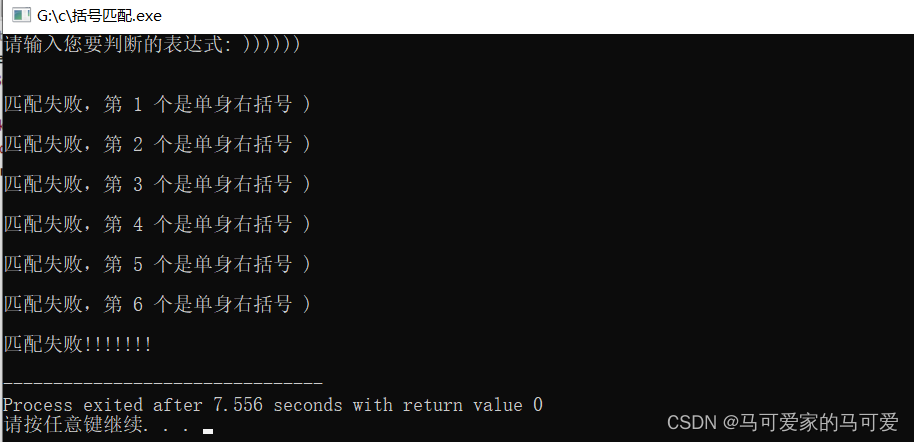
5、算法分析
此算法从头到尾扫描整个算式表达式中的每一个字符,若算式表达式的字符串长度是n,该算法的时间复杂度为O(n)。算法在运行时所占用的辅助空间主要取决于OPTR栈和OPAD栈的大小,显然他们的空间大小之和不会超过n,所以该算法的空间复杂度也是O(n)