該文章轉載
歐氏距離與餘弦相似度的比較
在數據挖掘中,相似性度量是個基礎且重要的問題,我們經常想得知兩個個體之間存在的差異大小,藉由一個合適的度量方式,幫助我們執行分群、分類等任務。在眾多度量方式,最耳熟能詳的莫過於歐式距離、餘弦相似度,這篇文章將帶領讀者初探兩者的原理及應用場景。
歐式距離
歐式距離或稱歐幾里得距離,一種簡單直觀且有效的距離度量方式。回想初中計算座標(x1,y1)、(x2,y2)兩點之間的距離,便是 (x1-x2)²+(y1-y2)²再將其開根號即得出結果。以數學表示,假設歐式空間中,存在點x =(x1,…,xn)和 點y =(y1,…,yn),以下的公式用以求出兩者之間的歐式距離。
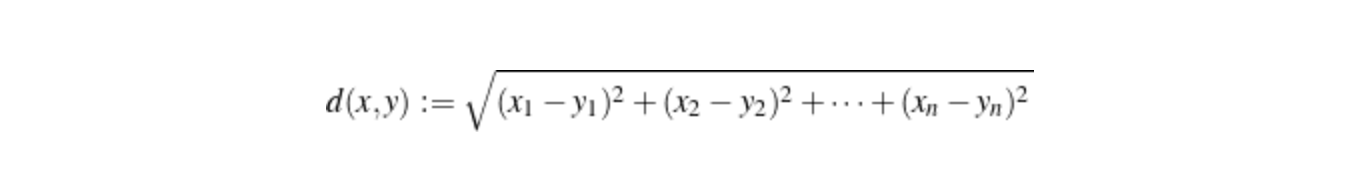
不難發現,歐式距離就是畢氏定理的一個推廣。
用python代碼實現歐式距離度量只消一行程式碼。假設vec1、vec2表示等長向量,則兩者之間的歐式距離如下 。
np.sqrt(sum(pow(vec1-vec2,2)))
餘弦相似度
餘弦相似度,顧名思義,藉由測量兩個向量夾角的餘弦值,來度量它們之間的相似性。向量之間夾角越小,表示兩個向量的方向越接近,方向一致時餘弦值為1;反之向量之間夾角越大,表示兩個向量的方向差異越大,方向相反時餘弦值為-1;至於呈現直角則如同下圖,夾角為90°,此時餘弦相似度的值為0。至此可以發現,餘弦相似度無關乎向量大小,重點是向量之間的方向。

餘弦相似度越大,表示個體之間越接近,與歐式距離度量概念相反,歐式距離是值越小,表示距離越近,個體越相似。餘弦相似度的衡量可由內積公式推導而來,數學表示如下。
內積公式

餘弦相似度公式

應用比較分析
歐氏距離體現數值上的絕對差異,而餘弦距離體現方向上的相對差異。
情境一
假設超商以顧客消費能力進行分群,指標是消費頻率及消費金額,區間一律落在(1,10)。客戶A的消費能力向量為(0,1),客戶B為(1,0),此時向量間的夾角呈現90度,餘弦相似度為0,因此餘弦距離很大,表示客戶A、B兩者不相似,這顯然不合理,反觀以歐氏距離度量只有1.41,表示客戶相似程度較高,顯然合理許多,因為兩個客戶的消費頻率、消費金額都很低,歐式距離考慮的正是數值上絕對的差異。
情境二
假設針對用戶基於對影視的偏好分群,衡量指標是用戶對影視的評分,分數區間(1,10),由於用戶評分標準不一致,不同用戶評分方式差異頗大,有人評分嚴格,認為給到5分便是極佳;有人則認為5分是最差勁的電影,至少給到7、8分。假設用戶A對兩個影視評分向量為(2,5),用戶B的評分向量為(4,10),以歐式距離衡量兩者用戶極為不相似,但以餘弦相似度衡量則可以視為同一群,顯然以後者度量比較恰當,因為餘弦相似度對於絕對值的差異不敏感,我們想知道的是用戶對於影視的相對偏好,因此只要偏好影視種類的比例相仿,餘弦相似度就會比較高,易於分為同一族群。