数组

一维数组

• 相同类型的数据元素的集合
• 允许元素值重复

二维数组

• 形式地表示为：(D,R)
• D={a
  
  _ij
  
  (i=0,1,…,m-1,j=0,1,…,n-1)}，是同类型数据元素的集合。
• a
  
  _ij
  
  是第i行第j列的数
• R={ROW, COL} 是数据元素上关系的集合。
• ROW是每一行上的列关系，COL是每一列上的行关系。

三维数组

• 是二维数组的数组
• 赋值顺序：000，001，010，011，
  
  100，101，110，111，
  
  200，201，210，211，
  
  …

n维数组

• 是n-1维数组的数组

数组的遍历

//二维数组
for(int i=0;i<n1*n2;i++)
{
    cout<<a[i/n2][i%n2]<<" ";
}

//三维数组
for(int i=0;i<n1*n2*n3;i++)
{
    cout<<a[i/(n2*n3)][(i/n3)%n2][i%n3]<<" ";
}

//四维数组
for(int i=0;i<n1*n2*n3*n4;i++)
{
    cout<<a[i/(n2*n3*n4)][(i/(n3*n4))%n2][(i/n4)%n3][i%n4]<<" ";
}

//n维数组
for(int i=0;i<n1*n2*n3*...*nn;i++)
{
    cout<<a[i/(n2*n3*n4*...nn)][(i/(n3*n4*...nn))%n2][(i/(n4*n5*...nn))%n3]...[(i/nn%n(n-1)][i%nn];
}

对称矩阵

• a
  
  _ij
  
  = a
  
  _ji
  
• 以对角线为对称轴
• 可划分为上三角矩阵和下三角矩阵

上三角矩阵

• 对角线及对角线以上的元素

下三角矩阵

• 对角线及对角线以下的元素

对称矩阵的压缩存储

• 将
  
  下三角矩阵
  
  按行存放于一个一维数组中，称为对称矩阵的压缩存储方式。
• 下三角矩阵中，第 i 行有 i 个元素（i=1..n），所以数组共有 n*(n+1)/2 个元素。
• 若 i>=j，数组元素A[i][j]在下三角矩阵中，在数组中的存放位置为 1+2+…+i+j = (i+1)* i/2+j
• 若 i < j，数组元素A[i][j]在上三角矩阵中，在数组中没有存放的位置，找到下三角矩阵中相同的数在数组中的位置k
  
  • 行号：满足 i*(i+1)/2 =< k < (i+1)*(i+2)/2
  • 列号：j = k – i*(i+1)/2

三对角矩阵的压缩存储

• 三对角矩阵中除主对角线及在主对角线上 下最临近的两条对角线上的元素外，所有其它元素均为0。总共有3n-2个非零元素
• 将三对角矩阵A中三条对角线上的元素按行存放在一维数组B中，且a
  
  ₀₀
  
  存放于B[0]。
• 0 =< i <= n-1，i-1 =< j <= i+1
• 元素 A[i][j] 在数组B中位置为 k = 2 * i + j

稀疏矩阵

• 矩阵中非零元素个数远远少于矩阵元素个数

广义表

定义

• n ( >= 0 )个表元素组成的有限序列
• 记作LS = (a
  
  ₀
  
  , a
  
  ₁
  
  , a
  
  ₂
  
  , …, a
  
  _n-1
  
  )
• LS是表名，a
  
  _i
  
  是表元素，它可以是表 (称为子表)，可以是数据元素(称为原子)。
• n为表的长度
• n = 0 的广义表为空表
• n > 0时，表的第一个表元素称为广义表的表头(head)，除此之外，其它表元素组成的表称为广义表的表尾(tail)。

例子：

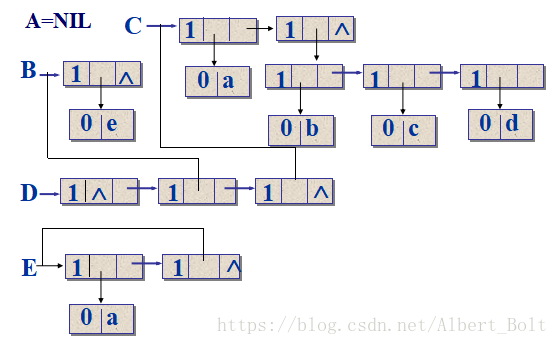
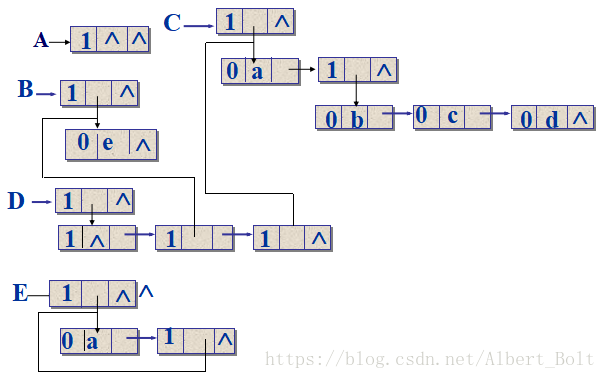
• A=( )：A是一个空表
• B=(e)：表B有一个原子
• C=(a,(b,c,d))：两个元素为原子a和子表(b,c,d)
• D=(A,B,C)：有三个元素均为列表
• E=(a,E)：递归的列表，包含两个元素，单元素a和子表，但该子表是其自身。所以，E相当于一个无限的广义表( a,(a,(a,…)))

存储结构

• tag为：标志域
• hp为：指示表头的指针域
• tp为：指示表尾的指针域
• atom为：值域
  
  
  
  
  
  
  
  

广义表的递归算法

• 广义表的深度（广义表中括号的重数）：原子的深度为零，空表的深度为1，其它情况下表长为各子表深度最大值加1。
• 复制广义表：如果原表为空表，则直接将新表置空，否则分别复制原表的表头和表尾。